ACM预备队-week7(DP1)

1.[NOIP2005 普及组] 采药

题目链接：P1048 [NOIP2005 普及组] 采药 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

01背包，可以利用滚动数组优化为一维。

#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int f[N];
int main()
{
    int T,M;
    cin>>T>>M;
    for(int i=1;i<=M;i++)
    {
        int v,w;
        cin>>v>>w;
        for(int j=T;j>=v;j--)
        {
            f[j]=max(f[j],f[j-v]+w);
        }
    }
    cout<<f[T];
    return 0;
}

2.最长上升子序列

题目链接：B3637 最长上升子序列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

如果数据范围是1e4数量级以上，就不能用朴素算法了，O(N²)的复杂度

#include <bits/stdc++.h>
using namespace std;
const int N=5010;
int a[N],f[N];
int n;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)cin>>a[i];
    for(int i=1;i<=n;i++)
    {
        f[i]=1;
        for(int j=1;j<i;j++)
            if(a[j]<a[i])
            {
                f[i]=max(f[i],f[j]+1);
            }
    }
    int ans=0;
    for(int i=1;i<=n;i++)ans=max(ans,f[i]);
    cout<<ans;
    return 0;
}

 3.最大子段和：

题目链接：P1115 最大子段和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

该算法更为简便之处是忽略了对子序列的寻找比较,而是根据规律直接找出最佳答案.

对于含有正数的序列而言,最大子序列肯定是正数,所以头尾肯定都是正数.我们可以从第一个正数开始算起,每往后加一个数便更新一次和的最大值;当当前和成为负数时,则表明此前序列无法为后面提供最大

子序列和,因此必须重新确定序列首项.

首先定义一个答案，必须在数据最小值范围之外，定义S是扫描到第i个数时，前 i-1 个数的最大子段和，将子段与0比较即可，反正是玄学。。。

#include <bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int a[N];
int main()
{
    int res=-1e9,n,s=0;
    cin>>n;
    for(int i=0;i<n;i++)cin>>a[i];
    for(int i=0;i<n;i++)
    {
        if(s<=0)s=0;
        s+=a[i];
        res=max(res,s);
    }
    cout<<res;
    return 0;
    
}

4.最长公共子序列(LCS)

题目链接：LCS - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

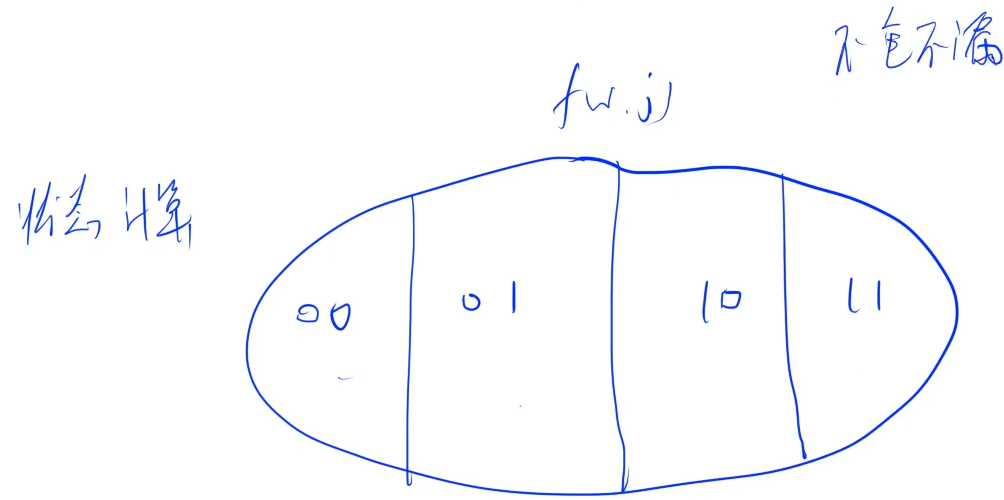
其中00表示不含i和j，01表示不含i但含j(这个j可能选也可能不选)，10表示含i但不含j(这个i可能选也可能不选)，11表示含i含j，但是，11有一个前提，就得是当a[i]==b[j]时。

00：f[i-1,j-1]           01：f[i-1,j]         10：f[i,j-1]       11：if(a[i]==b[j])f[i-1][j-1]+1

但是因为00其实就是01和10的子集，所以可以不写00，此时01和10其实不是真正意义的选与不选，但是最大值只要包括了而且没有越界，就算情况重复也不影响max值

因为此题还要输出路径，所以还得倒着来一遍。用res表示路径。

状态方程解释很清晰链接：最长公共子序列 - 动态规划 Longest Common Subsequence - Dynamic Programming_哔哩哔哩_bilibili

#include <iostream>
#include <algorithm>
#include <cstring>


using namespace std;

const int N = 1010;

int n, m;
char a[N], b[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    cin >> a + 1 >> b + 1;

    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= m; j ++)
        {
            if (a[i] == b[j]) f[i][j] =  f[i - 1][j - 1] + 1 ;
            else f[i][j] = max(f[i - 1][j], f[i][j - 1]);
            
        }
    cout << f[n][m] << endl;

    string res;
    // 一个倒序的过程
    for (int i = n, j = m; i && j; )
    {
        if (a[i] == b[j]) res += a[i], i --, j --;
        else if (f[i - 1][j] > f[i][j - 1]) i --;
        else j --;
    }

    reverse(res.begin(), res.end());

    cout << res << endl;
    return 0;
}