【游戏杂谈】(二)游戏开发
一. 客户端
1. 3D数学基础
1.1 向量代数
- 向量是具有大小和方向的物理量
- 可以用于表示空间中的点(坐标位置), 也可以表示力、位移和速度,还可以用来表示单个方向
- 一个 n 维向量可以表示为: V = < v1,v2,...,vn >
- 向量的叉积
- 区别与向量的点积计算结果是一个标量,差积计算结果是一个向量
- 叉积只能用于 3D 向量( 2D 向量没有叉积)
- 叉积计算公式:A * B = < AyBz - AzBx , AzBx - AxBz , AxBy - AyBx >
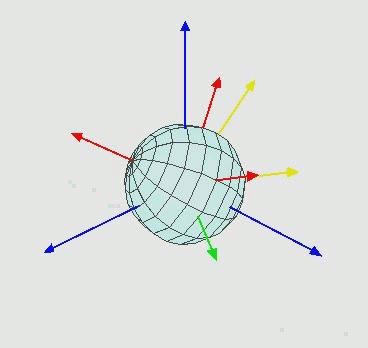
- 计算两个 3D 向量 A,B 的叉积,可以得到同时垂直于 A,B 向量的第三个向量
- 可以应用在计算机图形学中:给定平面上的一个点,及两个不同的切向量,可以计算出该点的法向量
![]()
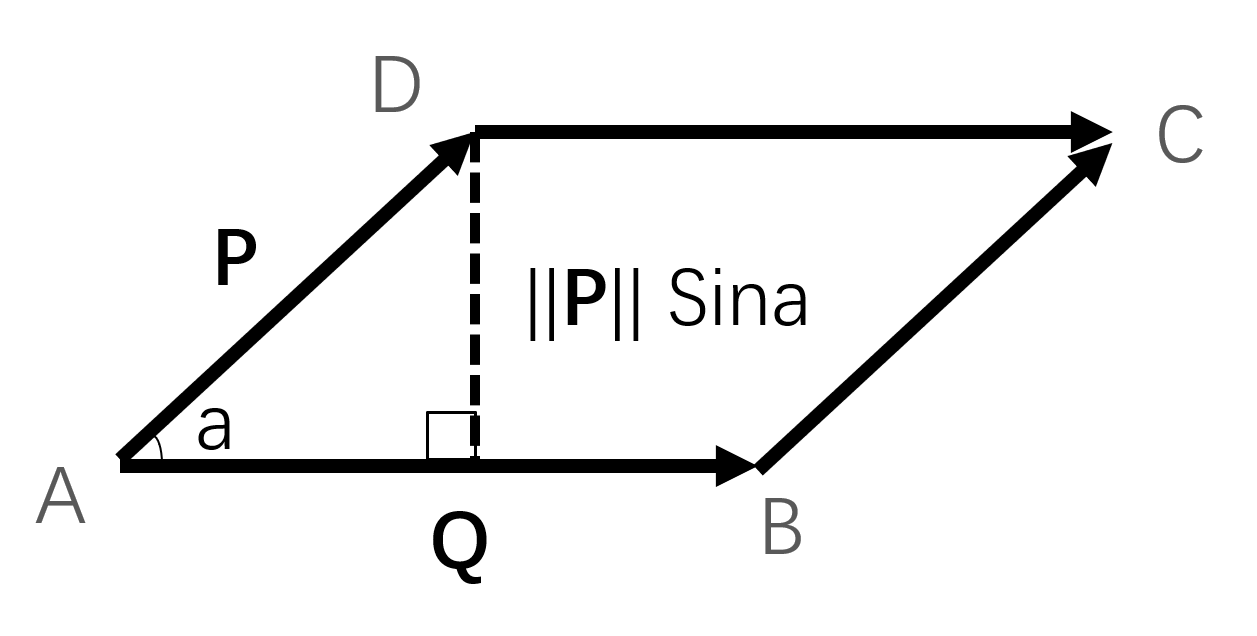
- 叉积对应的几何意义:|| P * Q|| = || P || || Q || Sina
- 该公式可以用于计算由 P 和 Q 组成的平行四边形或三角形的面积:平行四边形以 ||Q|| 为底,||P||Sina 为高,则面积为||P|| ||Q||Sina,等于两个向量叉积的模||P*Q||,而对应三角形ABD的面积为 ||P*Q|| / 2
![]()
- 该公式可以用于计算由 P 和 Q 组成的平行四边形或三角形的面积:平行四边形以 ||Q|| 为底,||P||Sina 为高,则面积为||P|| ||Q||Sina,等于两个向量叉积的模||P*Q||,而对应三角形ABD的面积为 ||P*Q|| / 2
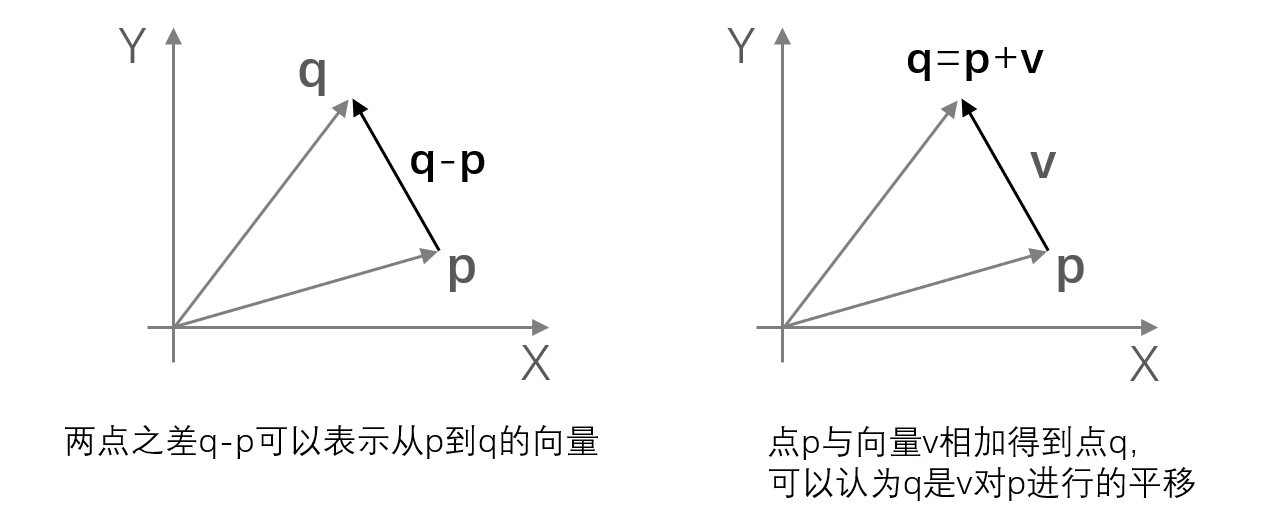
- 点
- 每个向量空间都可以通过一组向量的线性和得到,这组向量叫做该向量空间的基向量。如3D游戏编程中,组成空间(空间直角坐标系)的三个基向量分别是:(1,0,0),(0,1,0),(0,0,1)
- 使用向量来表示点的好处是,可以在代码中使用向量进行运算
![]()
1.2 矩阵代数
- 一个 m×n 矩阵,是一个 m 行 n 列的矩形实数数组。其中,行和列的数量指定了矩阵的维数,矩阵中的数值称为元素。我们使用 ij 来标识第 i 行和第 j 列的矩阵元素,当 m=n 时,称矩阵为方阵
- 假如是一个 4×3 的矩阵 F,如下:可以将矩阵的每一行视为一个向量。
![]()
- 同理,也可以将矩阵的每一列视为一个向量
![]()
- 矩阵具有诸多属性和运算,如标量乘法,矩阵加减法,矩阵乘法,单位矩阵,转置矩阵,逆矩阵和行列式等,可自行参考相应书籍资料
1.3 变换
- 线性变换
- 假定一个3D坐标系C,包含一个原点和三条坐标轴,其中有一个点P,表示为<x,y,z>,则 x,y,z 可以理解为从原点出发到点P;
- 再假定一个3D坐标系C`,其中的点<x`,y`,z`>可以通过对C中的坐标进行线性变换得到,变换函数如下公式所示:
![]()
- 假定 T=0,C的坐标轴基向量为:i=<1,0,0>,j=<0,1,0>,k=<0,0,1>
- ① 缩放
- 当一个系数 a 对向量P进行缩放变换时,变换公式:C` = aP
- 在3D空间中,也可以写成矩阵乘法的形式:
![]()
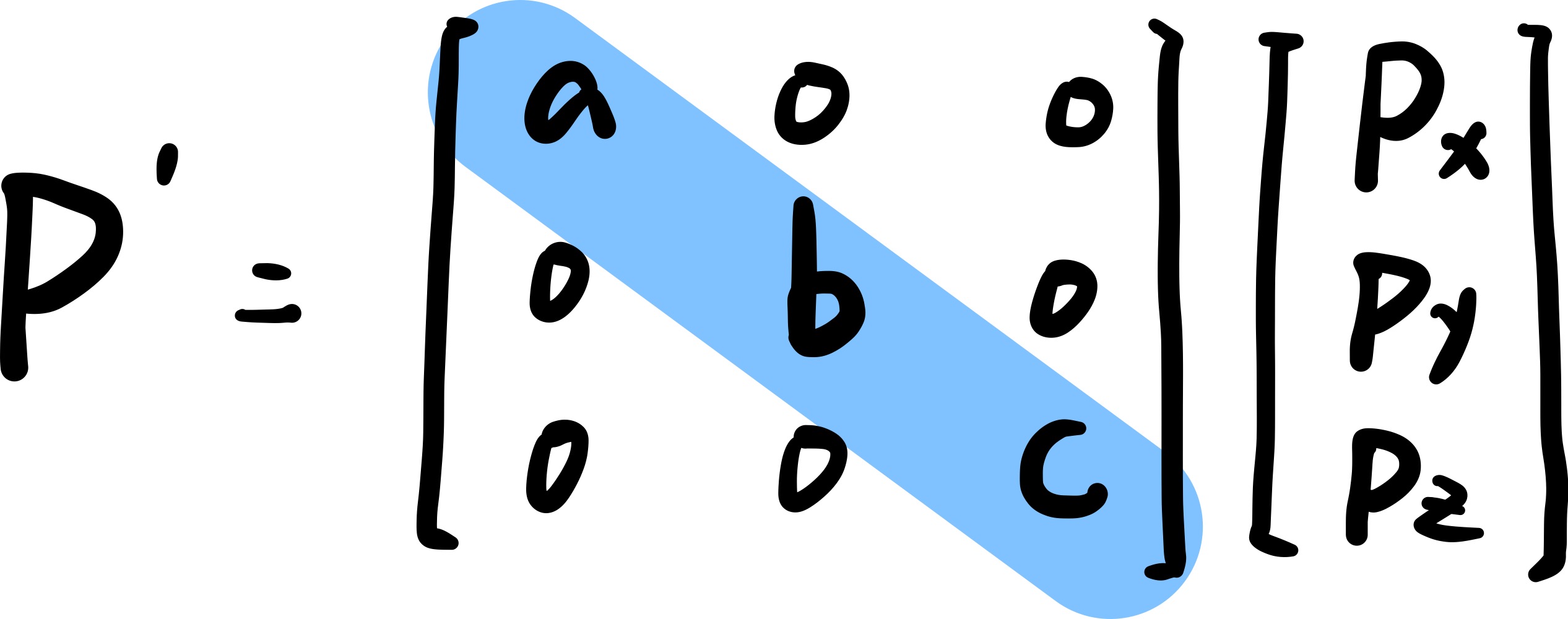
- 非等比缩放(矩阵的对角元素不相等)
![]()
- 同时,通过上面的公式可以用逆矩阵的方式,将点P`还原为初始点P
![]()
- ② 旋转
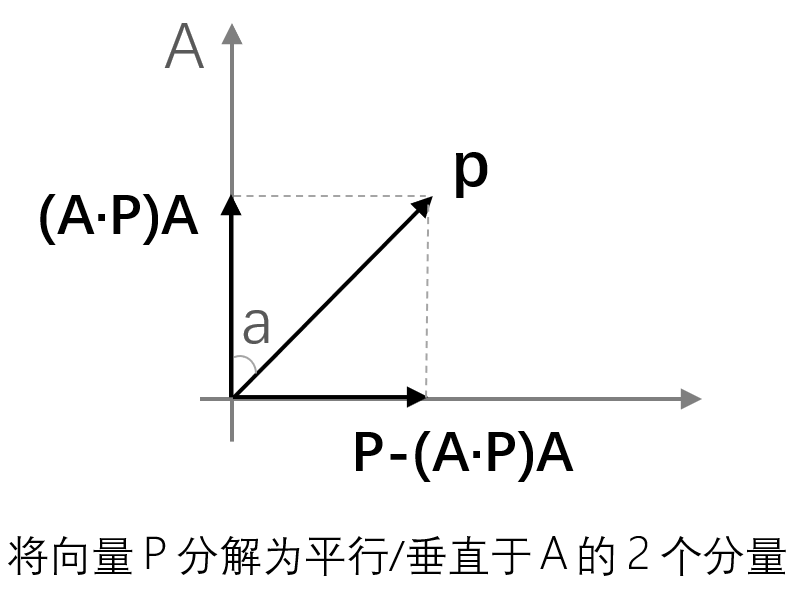
- 将向量P绕轴A旋转a角度,且假设 ||A||=1,则可以将向量P分解为分别平行与垂直A的2个分向量。
![]()
-
其中,(A·P)A 向量不受旋转影响,此问题的解答可以简化为先将 P-(A·P)A 垂直分量绕 A 轴旋转后,加上保持不变的平行分量即可
- 垂直分量绕 A 轴的旋转发生在垂直于 A 的平面,因此我们需要建立一个位于该旋转平面的2D坐标系,将垂直分量作为其中一个基向量,第二个基向量需要同时垂直于旋转轴 A 和垂直分量。设 a 为向量 P 和 A 的夹角,通过向量叉积 A x P,可以计算出一条同时垂直于 A 和 P 的向量,得到垂直分量旋转变换后的表示:(P-(A·P)A)cos a + (AxP)sin a
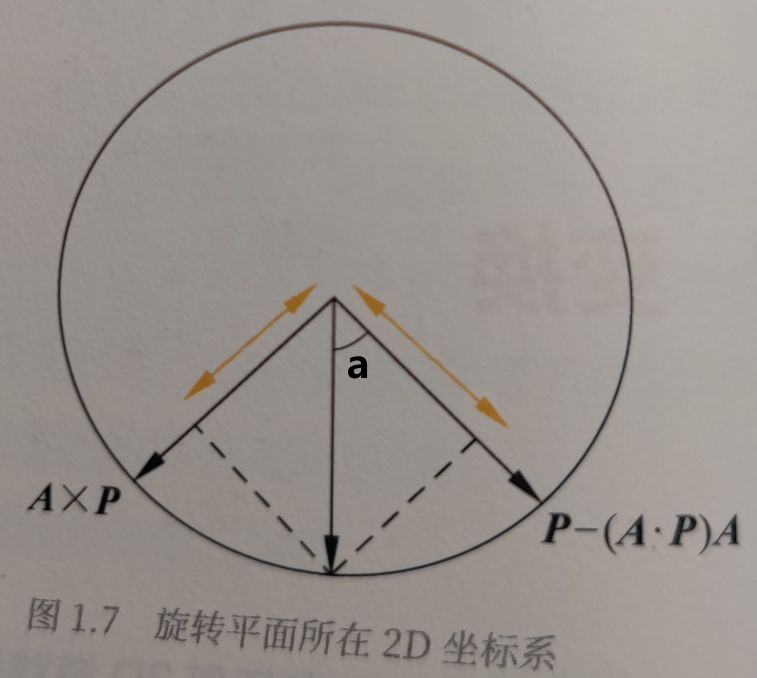
- 特别说明,cos a 和 sin a 分别表示垂直分量经过 a 角度旋转后,在我们构造的2D坐标系中基向量上的投影长度,如图:
![]()
-
加入平行分量,得到旋转后的向量:P`=Pcos a + (AxP)sin a + A(A·P)(1 - cos a)
-
将公式中的叉积和点积替换为对应的公式后,得到如下矩阵运算形式:
![]()
- 将向量P绕轴A旋转a角度,且假设 ||A||=1,则可以将向量P分解为分别平行与垂直A的2个分向量。
- ③ 平移
- 平移不会影响坐标系的坐标轴,只需要简单的加上一个偏移向量,没有办法写成一个3×3的矩阵形式
- 齐次坐标系统
- 如果需要将点 P 从一个坐标系变换到另一个坐标系中,同时考虑到多次缩放,旋转和平移,可以用齐次坐标系来表达向量,并使用一个4×4矩阵对其进行变换。
- 在齐次坐标系中,坐标点 P 被扩展为一个四维向量<x,y,z,w>,其中 w=1,将变换矩阵M和平行向量T合并成一个4×4的矩阵F:
![]()
- 若要将点P从齐次坐标系转换为原3D坐标系中,则使用公式:P=<x/w,y/w,z/w>
- 其中w不为0,对于坐标点来说,经过缩放,旋转,平移等线性变化后,实际上w保持1不变,而对于一些非线性变化(如投影变换等)会改变w的值
- 如果仍想使用4×4矩阵对方向进行变换操作,只需要使用<x,y,z,0>来表示齐次坐标系中的方向向量,这样矩阵中只有左上角3×3子矩阵 M 对计算结果有影响
- 在齐次坐标系中做向量运算,不会破坏坐标点和方向向量的定义。如 P` = P+V 表示点 P 沿方向向量 V 平移,得到一个新的点 P`,平移前后Pw = P` = 1;V ///= P` - P,表示点 P 指向点 P`的方向向量,Vw = 1
- 组合变换
- 假设需要对一个立方体进行多次线性变化(旋转R,缩放S,平移T),根据矩阵运算的结合律,可以得到更高性能的组合变换公式:Pi` = (RST)Pi,i=0,1,...,7
- 欧拉角
- 前文都是使用矩阵来表示旋转变化,虽然矩阵是一种比较适合计算机处理的表达形式,但缺点也比较明显:不支持直接插值,比较占用存储空间,人为阅读不直观等。除了旋转矩阵外,我们也可以使用欧拉角的形式来表达旋转变换
- 欧拉角:就是模型绕坐标系三个坐标轴的旋转角度,模型的任意旋转都可以分解为欧拉角的形式,且分解结果不唯一
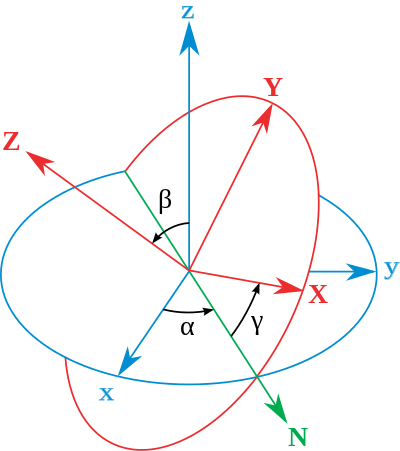
- 给定三个欧拉旋转角度( α , β , γ ) (\alpha,\beta,\gamma)(α,β,γ) 和 Z-X-Y顺序(蓝色坐标轴-上Z、左X、右Y)
![]()
![]()
-
优点
- 表述清晰易懂,可读性强,利于理解
- 缺点
- 万向节死锁:动态欧拉角有万向节死锁问题(第二个轴的旋转为 ±90°)。死锁会导致第一次旋转和第三次旋转等价,整个旋转表示系统被限制在只能绕竖直轴旋转,丢失了一个表示维度
- 不明确问题:三维空间中的任意一个方向都可以通过至少两种不同欧拉角表示,而在没有其他条件的约束的情况下,我们并不确定此时哪一种欧拉角的表述更为合理。例如:物体的原始方向(0,0,0)也可以用( 2 / 3 π , 0 , − 2 / 3 π ) (2/3\pi,0,-2/3\pi)(2/3π,0,−2/3π)来表示(由于此时 β \betaβ 是0,所以只要 α \alphaα 和 γ \gammaγ 的和为0,都可以表示出这个方向)
- 数据存储问题:通过旋转矩阵的表达式,记录这样一个变换,至少需要计算三个角的sin和cos值,也就是一共存储6个单位数据,对比四元数要多得多
- 给定三个欧拉旋转角度( α , β , γ ) (\alpha,\beta,\gamma)(α,β,γ) 和 Z-X-Y顺序(蓝色坐标轴-上Z、左X、右Y)
- 由此而引入了另一种常见旋转变换形式:四元数
- 四元数
- 相较于旋转矩阵,四元数有诸多优点:占用更小的存储空间、多次旋转变换连接需要更少的算术运算量、支持球形插值更有利于产生平滑的动画效果等
- 回忆一下高中时学的复数(一个复数由实部和虚部组成,即 x = a+bi,i 是虚数单位,且i平方等于-1)
- 四元数与复数类似,是简单的超复数,其所在空间是一个四维空间(相较于复数的二维空间),它的虚部包含了三个虚数单位<i,j,k>
- 一个四元数 q 可以表示为:q = <w,x,y,z> = w + xi + yj + zk
- 通常还可以将四元数写为更简单的形式:q = s + v(其中,s表示四元数中的标量部分,也即是w;v表示向量部分<x,y,z>)
- 如果给定一个单位长度的旋转轴 <x,y,z> 和一个角度 a ,则对应的四元数为:q = ((x,y,z)sin a/2 , cos a/2)
1.4 几何对象
1.5 光照和绘制
2. 图形渲染
2.1 渲染管线
2.2 光照
2.3 次世代渲染基础
3. 物理
4. 游戏中的动画系统
5. 特效
6. 音频
未完待续...



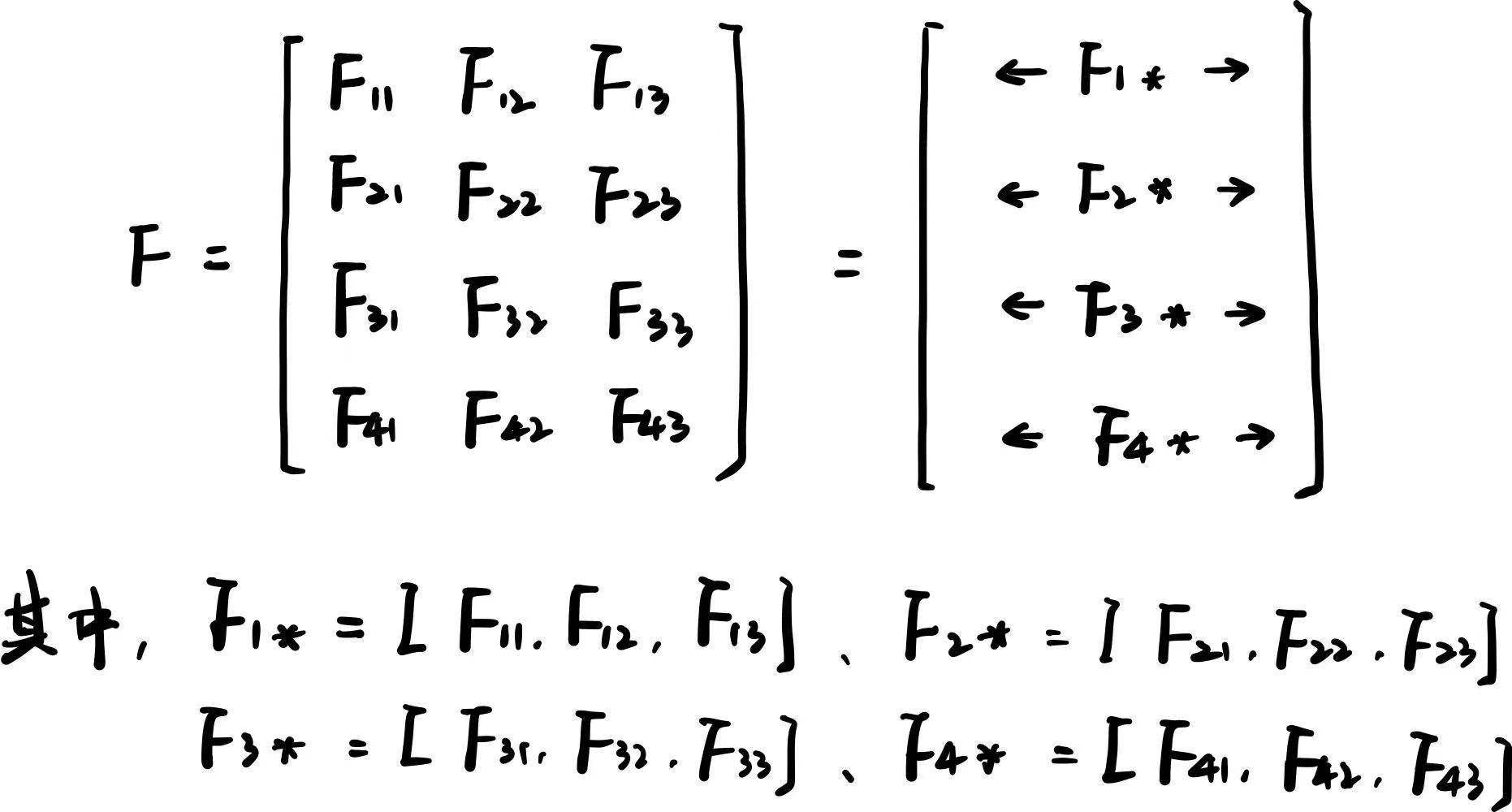
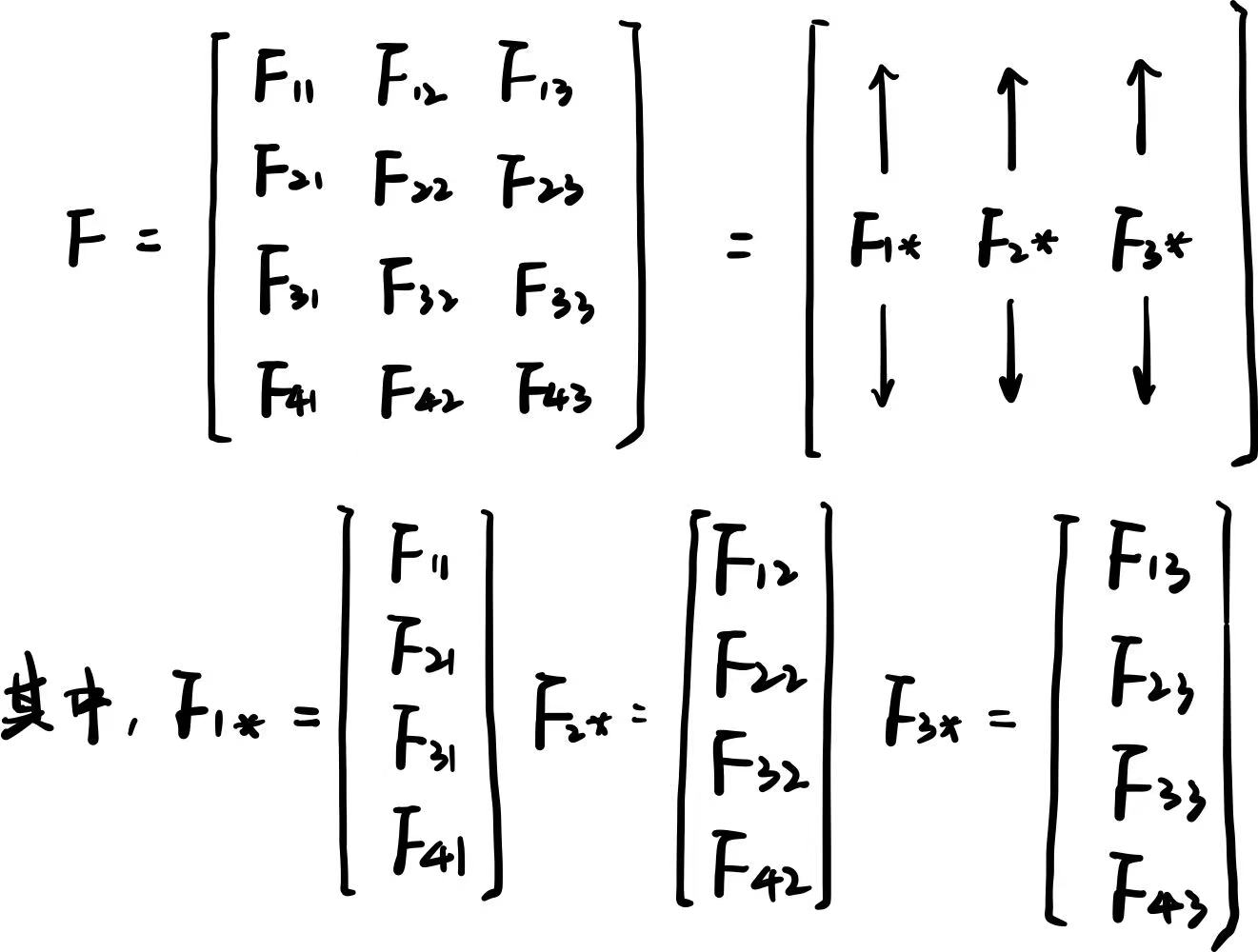




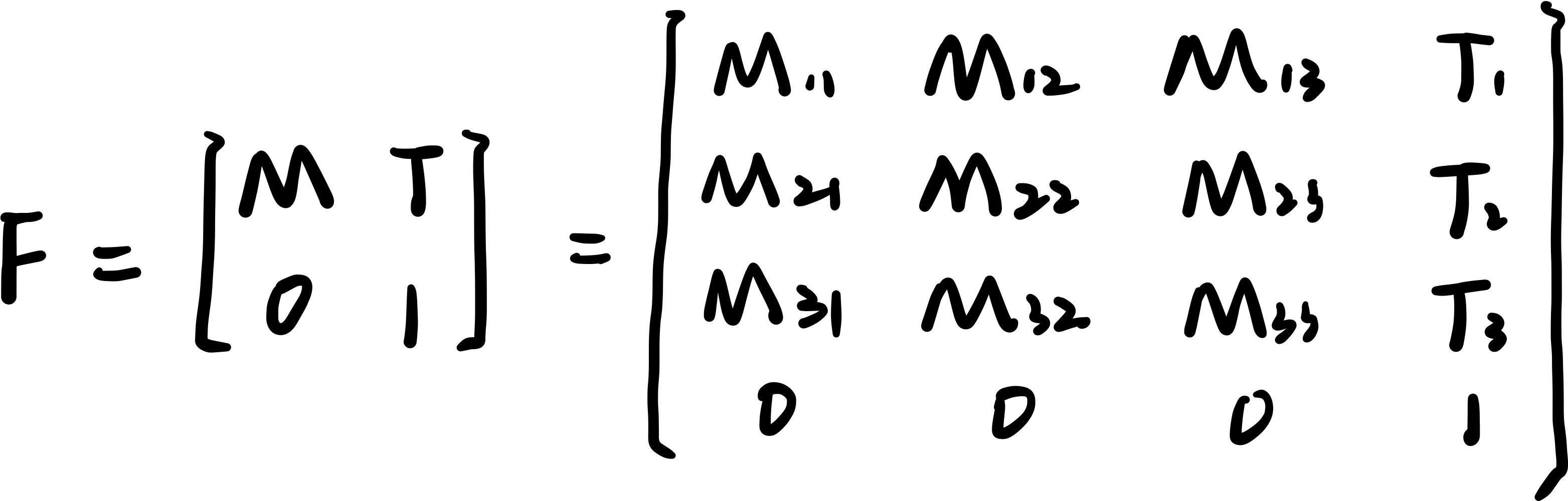

 浙公网安备 33010602011771号
浙公网安备 33010602011771号