luogu2544

luogu2544 数字迷阵

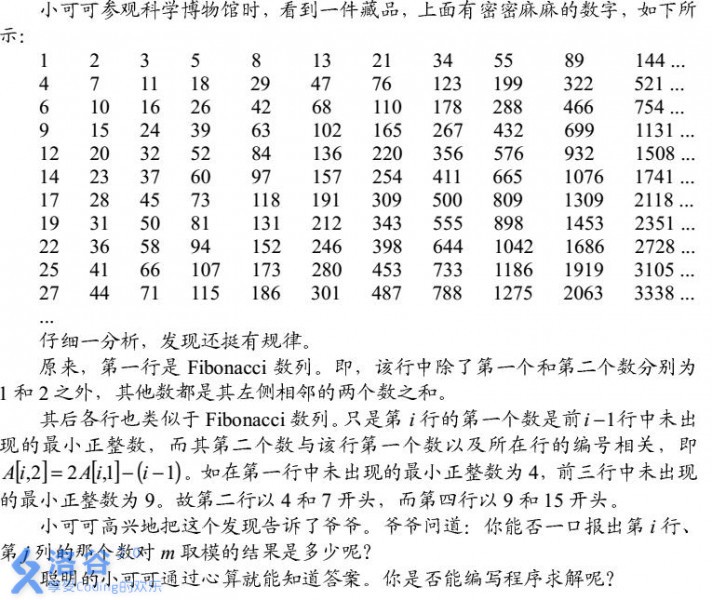
1 题目描述

2 分析

我们可以第一列的数有一个神奇的性质：

\[第i个行的第一个数=int(i*c^2)-1,c=\frac{1+\sqrt{5}}{2} \]

每行的第二个数明显有规律， \(2*第一个数-(i-1)\)

这样我们就找到了每行的开头两个数，剩余的数，我们可以用矩阵乘法来做。

3 代码

//
//  main.cpp
//  code
//
//  reated by prayer 胡 on 2020/8/24.
//  Copyright © 2020 prayer 胡. All rights reserved.
//

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
long long  n,m,mod;
struct matrix{
    long long  x[3][3];
    void init(){
        memset(x,0,sizeof(x));
    }
};
matrix operator * (matrix a,matrix b){
    matrix c;
    c.init();
    for(long long  i=0;i<2;i++)
        for(long long  j=0;j<2;j++)
            for(long long  k=0;k<2;k++)
                c.x[i][j]=(c.x[i][j]+a.x[i][k]*b.x[k][j])%mod;
    return c;
}
matrix ksm(matrix c,long long  p){
    matrix res;
    res.init();
    res.x[0][0]=res.x[1][1]=1;
    while (p){
        if(p&1) res=res*c;
        c=c*c;
        p>>=1;
    }
    return res;
}
int   main(){
    scanf("%lld%lld%lld",&n,&m,&mod);
    long long t=1LL*n*(6+2*sqrt(5.0))/4-1;
    long long p=2*t-(n-1);
    t%=mod;
    p%=mod;
    if(m==1)
        cout<<t<<endl;
    else if(m==2)
        cout<<p<<endl;
    else {
        matrix c;
        c.init();
        c.x[0][0]=c.x[0][1]=c.x[1][0]=1;
        matrix ans=ksm(c,m-2);
        cout<<(p*ans.x[0][0]+t*ans.x[1][0])%mod<<endl;
    }
    return 0;
}