多项式乘法loj 108

FFT

1 简述

FFT是专门用来求解多项式乘法的一个高效算法。 总所周知，朴素的多项式乘法的时间复杂度是\(O(n^2)\)，而FFT利用复数的知识做到了\(O(nlogn)\)。

2 点值表达式

设\(A(x)\)是一个n-1次方的多项式，那么把n个不同的x代入，一定可以得到n个y，这n对(x,y)唯一确定了该多项式的系数。由多项式可以求出点值表达式，由点值表达式可以求出这个多项式。

这里，我们把n作为2的幂次方存在。

我们发现，用点值表达式做多项式乘法是\(O(n)\)的，即\(A(x_i)=B(x_i)*C(x_i)\)。 所以把多项式先转换为点值表达式，然后就可以\(O(n)\)解决多项式乘法问题。

朴素的，把多项式转换为点值表达式也是\(O(n^2)\)的。

所以多项式乘法的瓶颈在于如果在更快的时间内把多项式转换为点值表达式。

这个就需要傅里叶变换了。

3 复数

复数是数学上一个很常见的概念，复数的特点是对负数进行开方。负数相加的规则是实部（x轴）和实部相加，虚部（y轴）和虚部相加。 复数乘法的规则是模长相乘，幅角相加。 下面略作证明：

\[z_1=r_1*(cos\theta+i*sin\theta),z_2=r_2*(cos\xi+i*sin\xi) \]

\[z_1*z_2=r_1*r_2*(cos\theta*cos\xi+i*cos\theta*sin\xi+i*sin\theta*sin\xi-sin\theta*sin\xi) \]

\[z_1*z_2=r_1*r_2*(cos(\theta+\xi)+i*sin(\theta+\xi)) \]

c++里面提供了复数的模板，可以直接进行加减乘除（相当于一个pair），当然我们也可以自己写。

#include<complex>
complex<double> x;

我们要用到的复数都是模长为1的复数，这样相乘的模长还是1，只有幅角进行了改变。 我们可以画一个单位圆，把这个圆平均进行n等分，每个点都表示一个复数。

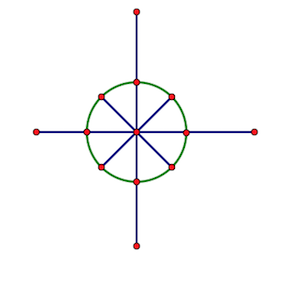
从（1，0）开始，我们逆时针旋转n个点从0开始编号，第k个点的复数记作\(w^{k}\)，明显的\(w^k=w*w*w...*w\)是k个w相乘，\(w^k\)对应的复数是\((cos(k\frac{2\pi}{n}),sin(k\frac{2\pi}{n}))\)。 我们把\(w^0,w^1,...w^{n-1}\)都代入到多项式里面，就得到了特殊的点值表达式，这个点值就叫做离散傅里叶变换。

其他的一些性质：

1. \(w^{2k}_{2n}=w^k_n\)，这个很明显，因为幅角是一样的。
2. \(w^{k+\frac{n}{2}}=-w^k\)，这个也很明显，因为差180度的复数刚好是相反数。

单位圆上的点有什么特殊性质么？

设\(y_0,y_1,...,y_{n-1}\)是多项式\(A(x)=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1}\)的离散傅里叶变换，我们再设一个多项式\(B(x)=y_0+y_1x+y_2x^2+...+y_{n-1}x^{n-1}\)，现在我们把上面的n个单位根的倒数，即\(w^0_n,w^{-1}_n,w^{-2}_n,...\)作为x代入到B里面去，得到一个新的离散傅里叶变换\((z_0,z_1,z_2,....)\)。

\[z_k=\sum_{i=0}^{n-1}y_i(w^{-k}_n)^i \]

\[z_k=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_jx^j_i)(w^{-k}_n)^i \]

\[z_k=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j(w^i_n)^j)(w^{-k}_n)^i \]

\[z_k=\sum_{j=0}^{n-1}a_j(\sum_{i=0}^{n-1}(w^{j-k})^i) \]

\[\sum_{i=0}^{n-1}(w^{j-k})^i,这个是可以求出来的。 \]

当\(j=k\)时，答案是n，如果\(j \ne k\)，那么根据等比数列求和公式：\(\frac{1-(w^{j-k})^n}{1-w^{j-k}}=0\)

所以\(z_k=na_k\)，所以\(a_k=\frac{z_k}{n}\)

总结

• 把多项式A(x)的离散傅里叶变换的结果作为另一个多项式B(x)的系数，取单位根的倒数作为x代入B(x)，得到的点值再除以n，就是A(x)的各项系数。
• 从而实现了傅里叶变换的逆变换，把点值转换为系数。
• 这个就是傅里叶变换神奇的性质。

4 离散傅里叶变换

朴素的傅里叶变换还是太慢了，所以我们要进行快速的傅里叶变换，借助于分治的思想。

我们设：

\[A(x)=(a_0+a_1x+a_2x^2+...a_{n-1}x^{n-1}) \]

把每个\(w^k_n\)代入，然后把A(x)按照下标分成奇偶两半部分。

\[A(x)=(a_0+a_2x^2+...+a_{n-2}x^{n-2})+(a_1x+a_3x^3+...+a_{n-1}x^{n-1}) \]

设有多项式：

\[A_1(x)=a_0+a_2x+...+a_{n-2}x^{\frac{n}{2}-1} \]

\[A_2(x)=a_1+a_3x+...+a_{n-1}x^{\frac{n}{2}-1} \]

于是：\(A(x)=A_1(x^2)+xA_2(x^2)\)

如果\(k<\frac{n}{2}\)，把\(w^k_n\)代入：

\[A(w^k_n)=A_1(w^{2k}_n)+w^k_nA_2(w^{2k}_n) \]

\[=A_1(w^k_{\frac{n}{2}})+w^k_nA_2(w^{k}_{\frac{n}{2}}) \]

那么对于\(A(w^{k+\frac{n}{2}})\):

\[A(w^{k+\frac{n}{2}})=A_1(w^{2k+n}_n)+w^{k+\frac{n}{2}}A_2(w^{2k+n}_n) \]

\[=A_1(w^k_{\frac{n}{2}}\times w^n_n)-w^k_nA_2(w^k_{\frac{n}{2}}\times w^n_n) \]

\[=A_1(w^k_{\frac{n}{2}})-w^k_nA_2(w^k_{\frac{n}{2}}) \]

于是问题就变成我们只要先计算出\(\frac{n}{2}\)时候的答案就可以了。

#include<bits/stdc++.h>
using namespace std;  
int const N=2e5+10;  
double const PI=asin(1.0)*2; 
typedef complex<double> cp; 
cp tmp[N<<1],a[N<<1],b[N<<1];  
int n,m,ans[N<<1];  
cp c(int n,int k){
	return cp(cos(2*k*PI/n),sin(2*k*PI/n));  
}  
void fft(cp *a,int n,int inv){
	if(n==1) return;  
	int m=n/2;  
	for(int i=0;i<m;i++){
		tmp[i]=a[2*i];  
		tmp[i+m]=a[2*i+1];  
	}  
	for(int i=0;i<n;i++) a[i]=tmp[i];  
	fft(a,m,inv);  
	fft(a+m,m,inv);  
	for(int i=0;i<m;i++){
		cp x=c(n,i);  
		if(inv) x=conj(x);  
		tmp[i]=a[i]+x*a[i+m];  
		tmp[i+m]=a[i]-x*a[i+m];  
	}
	for(int i=0;i<n;i++)  
		a[i]=tmp[i];  
}
int main(){
	scanf("%d%d",&n,&m); 
	for(int i=0;i<=n;i++) 
		scanf("%lf",&a[i].real());  
	for(int i=0;i<=m;i++) 
		scanf("%lf",&b[i].real());  
	int k=1;  
	while (k<n+m+1) k*=2;  
	fft(a,k,0); 
	fft(b,k,0);  
	for(int i=0;i<k;i++)  
		a[i]*=b[i];  
	fft(a,k,1);  
	for(int i=0;i<=n+m;i++)  
		printf("%d ",int(a[i].real()/k+0.5)); 
	return 0; 
}