[Atcoder] ABC244

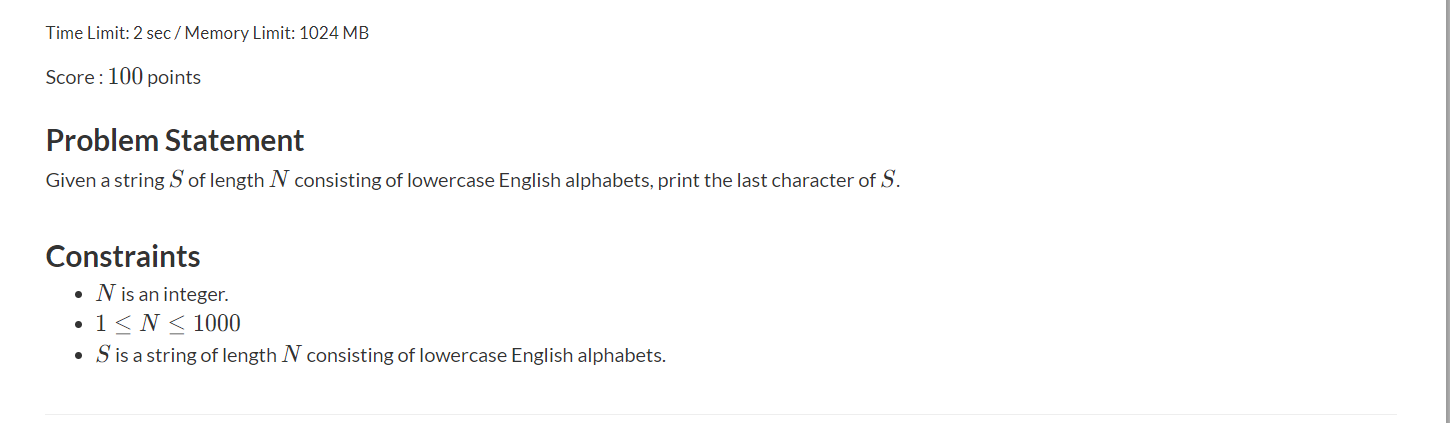
A - Last Letter
思路
输出字符串的最后一个字符
代码
#include<bits/stdc++.h>
#include <iostream>
#include <ctime>
using namespace std;
//==========================================
const int maxn = 1e5+5;
signed main(signed argc, char const *argv[])
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
#ifdef LOCAL
freopen("in.in", "r", stdin);
freopen("out.out", "w", stdout);
#endif
//======================================
string str;
int n;
cin >> n;
cin >> str;
cout << str[str.length() - 1] << endl;
//======================================
return 0;
}
/*DETAILS
*/
B - Go Straight and Turn Right

给出一个字符串,S代表直走,R代表转方向90度
求最后的x,y的坐标
思路
直接模拟即可
代码
#include<bits/stdc++.h>
#include <iostream>
#include <ctime>
using namespace std;
//==========================================
const int maxn = 1e5+5;
int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};
signed main(signed argc, char const *argv[])
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
#ifdef LOCAL
freopen("in.in", "r", stdin);
freopen("out.out", "w", stdout);
#endif
//======================================
int n;
string str;
cin >> n;
cin >> str;
int len = str.length();
int flag = 2;
int x = 0, y = 0;
for(int i = 0; i < len; i ++) {
if(str[i] == 'R') {
if(flag == 1) flag = 2;
else if(flag == 2) flag = 3;
else if(flag == 3) flag = 4;
else if(flag == 4) flag = 1;
}
else {
//cout << flag << endl;
x += dx[flag - 1], y += dy[flag - 1];
//cout << x << " " << y << endl;
}
}
cout << x << " " << y << endl;
//======================================
return 0;
}
/*DETAILS
*/
C - Yamanote Line Game

交互题,有1~2n+1共2n+1个数字,你和对手轮流说出一个没说过的数字,直到最后没数字可以说,模拟这个过程.
思路
注意输入输出的顺序即可,每次出现一个数字就在mp里标记掉,每次循环找没出现的数字输出
当输入为0的时候break
代码
#include<bits/stdc++.h>
#include <iostream>
#include <ctime>
using namespace std;
//==========================================
const int maxn = 1e5+5;
map<int, int> mp;
signed main(signed argc, char const *argv[])
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
//======================================
int n;
cin >> n;
int tmp;
int t = 2 * n - 1;
while(t --) {
for(int i = 1; i <= 2 * n + 1; i ++) {
if(!mp[i]) {
cout << i << endl;
mp[i] = 1;
fflush(stdout);
break;
}
}
cin >> tmp;
if(tmp == 0) break;
mp[tmp] = 1;
}
//======================================
return 0;
}
D - Swap Hats

给出三个人当前戴的帽子颜色和应该戴的帽子颜色,问能否在交换1e18次后三个人都是应该戴的帽子的颜色
思路
给出的s1,s2,s3是R,G,B的排列,t也是
那么按是否相同来划分,只会出现四种情况
都不相同, 如:s1 != t1, s2 != t2, s3 != t3
有一个相同,如:s1 == t1, s2 != t2, s3 != t3
有两个相同,如:s1 == t1, s2 == t2, s3 != t3
三个都相同,如:s1 == t1, s2 == t2, s3 == t3
题目要求必须交换1e18次
模拟一下就可以发现,只有在一个相同的情况下才会失败,其余都是成功
代码
#include<bits/stdc++.h>
#include <iostream>
#include <ctime>
using namespace std;
//==========================================
const int maxn = 1e5+5;
signed main(signed argc, char const *argv[])
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
//======================================
char s1, s2, s3;
char t1, t2, t3;
int fg = 0;
cin >> s1 >> s2 >> s3;
cin >> t1 >> t2 >> t3;
if(s1 == t1) fg ++;
if(s2 == t2) fg ++;
if(s3 == t3) fg ++;
if(fg == 1) cout << "No" << endl;
else cout << "Yes" << endl;
//======================================
return 0;
}
E - King Bombee

给出n个点,m条边的无向图,问满足以下条件的路径数
1、Ai是1~n之间的整数
2、A0=s
3、Ak=t
4、Ai~Ai+1之间有边连接
5、x号节点出现的次数是偶数(可能是0)
思路
一共最多是2000个点,2000条边,而路径数会很大,可以尝试去dp路径数
发现是可行的
我们可以令dp[i][j]表示走到第i个节点的步数为j的路径数
但是这样肯定不够,题目还有一个经过x点的次数不能是奇数的条件
所以就可以多加一维来表示经过x点的次数是奇数次还是偶数次
那么状态就为dp[i][j][z]表示走到第i个节点的步数为j,且z=1时表示经过x节点的次数是奇数次,z=0时表示经过x节点的次数是偶数次
状态转移方程就为,当u!=x时,dp[i][j][z] += dp[u][j - 1][z];
当u==x时,dp[i][j][z] += dp[u][j - 1][z ^ 1];
边界条件是从s号节点开始走,那么就是dp[s][1][0] = 1;
最终答案就是走到t号节点的步数为k+1且经过x号节点的次数为偶数次的路径数,即dp[t][k + 1][0]
代码
#include<bits/stdc++.h>
#include <iostream>
#include <ctime>
using namespace std;
//==========================================
const int maxn = 2010, mod = 998244353;
int e[2 * maxn], ne[2 * maxn], h[maxn], idx;
void add(int x, int y) {
e[idx] = y, ne[idx] = h[x], h[x] = idx ++;
}
int dp[maxn][maxn][3];
signed main(signed argc, char const *argv[])
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
#ifdef LOCAL
freopen("in.in", "r", stdin);
freopen("out.out", "w", stdout);
#endif
//======================================
int n, m, k, s, t, x;
cin >> n >> m;
cin >> k >> s >> t >> x;
int a, b;
memset(h, -1, sizeof h);
for(int i = 1; i <= m; i ++) {
cin >> a >> b;
add(a, b);
add(b, a);
//dp[a][b] = 1;
//dp[b][a] = 1;
}
dp[s][1][0] = 1;
for(int j = 2; j <= k + 1; j ++) {
for(int i = 1; i <= n; i ++) {
for(int z = h[i]; z != -1; z = ne[z]) {
int u = e[z];
if(u != x) {
dp[i][j][0] += dp[u][j - 1][0];
dp[i][j][0] %= mod;
dp[i][j][1] += dp[u][j - 1][1];
dp[i][j][1] %= mod;
}
else {
dp[i][j][0] += dp[u][j - 1][1];
dp[i][j][0] %= mod;
dp[i][j][1] += dp[u][j - 1][0];
dp[i][j][1] %= mod;
}
}
}
}
//cout << dp[s][k] << " " << dp[k][t] << endl;
cout << dp[t][k + 1][0] % mod << endl;
//======================================
return 0;
}
F - Shortest Good Path

给出一个n个点m条边的无向图,还有一个长度为n的01序列S
找出满足以下条件的最短路径长度之和
1、若Si=0,那么路径中出现了偶数个i
2、若Si=1,那么路径中出现了奇数个i
思路
这题其实还没搞特别懂,后面想透彻了再完善吧。。。
状压dp
f[i][j]表示当前状态为i,路径中最后一个点在j的最短路径长度,i中第k位为0说明这个点在路径中有偶数个,为1说明有奇数个。
代码
#include<bits/stdc++.h>
#include <iostream>
#include <ctime>
using namespace std;
//==========================================
const int maxn = 17, INF = 0x3f3f3f3f;
typedef long long ll;
typedef pair<int, int> PII;
vector<int> g[maxn];
int f[1 << maxn][maxn];
signed main(signed argc, char const *argv[])
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
#ifdef LOCAL
freopen("in.in", "r", stdin);
freopen("out.out", "w", stdout);
#endif
//======================================
int n, m;
cin >> n >> m;
while(m --) {
int a, b;
cin >> a >> b;
a --, b --;
g[a].push_back(b), g[b].push_back(a);
}
memset(f, 0x3f, sizeof f);
queue<PII> q;
for(int i = 0; i < n; i ++) {
f[1 << i][i] = 1;
q.push({1 << i, i});
}
while(!q.empty()) {
auto t = q.front();
q.pop();
int state = t.first, ed = t.second;
for(auto e : g[ed]) {
int nstate = state ^ (1 << e);
if(f[nstate][e] == INF) {
f[nstate][e] = f[state][ed] + 1;
q.push({nstate, e});
}
}
}
ll res = 0;
for(int i = 1; i < (1 << n); i ++) {
res += *min_element(f[i], f[i] + n);
}
cout << res << endl;
//======================================
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号