暑假补题 - Yukino酱～

https://ac.nowcoder.com/acm/contest/33186/D

使弦长最长，则弧形最长
使圆心角最大，则弦长最长
连接弦两端点作为直角三角形的斜边，从一个端点往另一个端点所在的射线作垂线，得到直角三角形
容易发现，炮管射线垂直于发射点与圆心的连线时, 圆心角最大，弦长最长，弧形最长
注意要setprecision，不然会产生误差

 1 #define _CRT_SECURE_NO_WARNINGS
 2 #include <bits/stdc++.h>
 3 #define int long long
 4 using namespace std;
 5 const int maxn = 2e6 + 5;
 6 const int mod = 1e9 + 7;
 7 
 8 signed main() {
 9     ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
10     int T; cin >> T; while (T--) {
11         double R, x, y, r;
12         cin >> R >> x >> y >> r;
13         x = sqrt(x * x + y * y);
14         double x1 = x - r, x2 = x + r;
15         double angle = acos(x1 / R) - acos(x2 / R);
16         cout << setprecision(13) << fabs(angle * R) << endl;
17     }
18     return 0;
19 }

https://ac.nowcoder.com/acm/contest/33187/g

题意：给出 n ，要求构造出一个长度为 n 的全排列，满足该全排列的max(最长上升子序列长度，最长下降子序列长度)最小。

将排列分成 2 种块，容易猜想每种块的长度为 n ** (1 / 2)
按根号分块进行构造即可

 1 #define _CRT_SECURE_NO_WARNINGS
 2 #include <bits/stdc++.h>
 3 #define int long long
 4 using namespace std;
 5 const int maxn = 2e6 + 5;
 6 
 7 signed main() {
 8     ios::sync_with_stdio(false); cin.tie(0), cout.tie(0);
 9     int T; cin >> T; while (T--) {
10         vector<int> a;
11         int n; cin >> n;
12         int t = sqrt(n - 1) + 1;
13         int top = n;
14         for (int i = 1; i <= n; i++) {
15             a.push_back(top--);
16             if (a.size() == t) {
17                 for (int j = a.size() - 1; j >= 0; j--)
18                     cout << a[j] << " ";
19                 a.clear();
20             }
21         }
22         for (int j = a.size() - 1; j >= 0; j--) cout << a[j] << " ";
23         cout << "\n";
24     }
25 
26     return 0;
27 }

https://ac.nowcoder.com/acm/contest/33187/l

题意：有 n 个世界，每个世界是一张简单有向图。从这些世界中选择一个子段进行游戏，规则为从 1 出发，每个世界可以原地不动或经过一条边，到达点 m 即为胜利。

要求选出一个尽可能短的子段，使得存在至少一种方案可以胜利。
观察数据范围，发现遍历每个世界的每条边为2e7，考虑暴力（dp）
注意空间被卡，需要用滚动数组

 1 #define _CRT_SECURE_NO_WARNINGS
 2 #include <bits/stdc++.h>
 3 //#define int long long
 4 using namespace std;
 5 const int maxn = 2e3 + 5;
 6 const int INF = 0x3f3f3f3f;
 7 // 偶数的世界由相邻上一个奇数世界转移，滚起来了
 8 int dp[2][maxn];
 9 
10 signed main() {
11     ios::sync_with_stdio(false); cin.tie(0), cout.tie(0);
12     int ans = INF;
13     int n, m; cin >> n >> m;
14     // 初始化
15     for (int i = 1; i <= m; i++) dp[0][i] = dp[1][i] = INF;
16     dp[0][1] = 0;
17     for (int i = 1, p = 0, e; i <= n; i++) {
18         p ^= 1; cin >> e;
19         for (int j = 1; j <= m; j++) dp[p][j] = dp[p ^ 1][j] + 1;
20         for (int j = 1; j <= e; j++) {
21             int u, v; cin >> u >> v;
22             // 注意题目的 "and wants to choose a continuous subsegment of them to form a new level"
23             // 可能选取其他的世界的起点开始转移，没看见wa了
24             if (u == 1) dp[p][v] = 1;
25             else dp[p][v] = min(dp[p][v], dp[p ^ 1][u] + 1);
26         }
27         ans = min(ans, dp[p][m]);
28     }
29     if (ans == INF) cout << -1 << endl;
30     else cout << ans << endl;
31     return 0;
32 }

https://ac.nowcoder.com/acm/contest/33188/A

题意 : 有两棵节点数为N的树A, B, 树中节点由1~n编号, 每个节点有一权值, 有k可个关键点
问有多少种方案, 仅去掉一个关键点, 使得剩余关键点在树A中lca的权值大于树B的权值

只用取这些点中dfs序最小和最大的两个点来求最近公共祖先就行，LCA板子题

 1 #define _CRT_SECURE_NO_WARNINGS
 2 #include <bits/stdc++.h>
 3 #define int long long
 4 using namespace std;
 5 const int maxn = 2e5 + 50;
 6 //deep数组记录的是树上每个节点的深度，fa数组记录的是每个点的父节点，这两个是倍增lca需要的
 7 int deepA[maxn], faA[maxn][31], deepB[maxn], faB[maxn][31];
 8 //st数组记录每个点的dfs序，w数组记录每个点的权值
 9 int stA[maxn], stB[maxn], wA[maxn], wB[maxn];
10 vector<int>treeA[maxn], treeB[maxn];
11 bool cmpA(int a, int b){ return stA[a] < stA[b];}
12 bool cmpB(int a, int b){ return stB[a] < stB[b];}
13 
14 void dfsA(int root, int fno, int& cnt) {
15     faA[root][0] = fno;
16     stA[root] = cnt++;
17     deepA[root] = deepA[faA[root][0]] + 1;
18     for (int i = 1; i < 31; ++i) faA[root][i] = faA[faA[root][i - 1]][i - 1];
19     int sz = treeA[root].size();
20     for (int i = 0; i < sz; ++i) {
21         if (treeA[root][i] == fno) continue;
22         dfsA(treeA[root][i], root, cnt);
23     }
24 }
25 void dfsB(int root, int fno, int& cnt) {
26     faB[root][0] = fno;
27     stB[root] = cnt++;
28     deepB[root] = deepB[faB[root][0]] + 1;
29     for (int i = 1; i < 31; ++i) faB[root][i] = faB[faB[root][i - 1]][i - 1];
30     int sz = treeB[root].size();
31     for (int i = 0; i < sz; ++i) {
32         if (treeB[root][i] == fno) continue;
33         dfsB(treeB[root][i], root, cnt);
34     }
35 }
36 int lcaA(int x, int y) {
37     if (deepA[x] > deepA[y]) swap(x, y);
38     int tmp = deepA[y] - deepA[x], ans = 0;
39     for (int j = 0; tmp; ++j, tmp >>= 1)
40         if (tmp & 1) y = faA[y][j];
41     if (y == x) return x;
42     for (int j = 30; j >= 0 && y != x; --j)
43         if (faA[x][j] != faA[y][j]) x = faA[x][j], y = faA[y][j];
44     return faA[x][0];
45 }
46 
47 int lcaB(int x, int y) {
48     if (deepB[x] > deepB[y]) swap(x, y);
49     int tmp = deepB[y] - deepB[x], ans = 0;
50     for (int j = 0; tmp; ++j, tmp >>= 1)
51         if (tmp & 1) y = faB[y][j];
52     if (y == x) return x;
53     for (int j = 30; j >= 0 && y != x; --j) 
54         if (faB[x][j] != faB[y][j]) x = faB[x][j], y = faB[y][j];
55     return faB[x][0];
56 }
57 
58 signed main(){
59     ios::sync_with_stdio(false); cin.tie(0), cout.tie(0);
60     int n, m; cin >> n >> m;
61     vector<int>ansA(m), ansB(m);
62     for (int i = 0; i < m; i++) cin >> ansA[i], ansB[i] = ansA[i];
63     for (int i = 1; i <= n; i++) cin >> wA[i];
64     for (int i = 2, x; i <= n; i++)
65         cin >> x, treeA[x].push_back(i);
66     int cnt = 1;
67     dfsA(1, 0, cnt);
68     for (int i = 1; i <= n; i++) cin >> wB[i];
69     for (int i = 2, x; i <= n; i++)
70         cin >> x, treeB[x].push_back(i);
71     cnt = 1;
72     dfsB(1, 0, cnt);
73     //按照dfs序对k集合的点进行升序排序
74     sort(ansA.begin(), ansA.end(), cmpA);
75     sort(ansB.begin(), ansB.end(), cmpB);
76     cnt = 0;
77     //我们以A树的k集合为标准枚举所有的点
78     for (int i = 0; i < m; i++) {
79         //x记录k集合中dfs序最小的点，y记录最大的点
80         int xA = ansA[0], yA = ansA[m - 1], xB = ansB[0], yB = ansB[m - 1];
81         //如果最大的点被删除，我们取第二大的
82         if (i == 0)xA = ansA[1];
83         //如果最小的点被删除，我们取第二小的
84         else if (i == m - 1)yA = ansA[m - 2];
85         if (xB == ansA[i])xB = ansB[1];
86         else if (yB == ansA[i])yB = ansB[m - 2];
87         //求的两个树的最近公共祖先
88         int xlca = lcaA(xA, yA), ylca = lcaB(xB, yB);
89         if (wA[xlca] > wB[ylca])cnt++;
90     }
91     cout << cnt << "\n";
92     return 0;
93 }

https://ac.nowcoder.com/acm/contest/33189/N

题意：任意两元素按位与和按位或，并将那两个元素替换成结果，直至数组元素不变，求方差

当元素不变的时候，1尽量聚集在一个数，0则在另一个，打表或模拟很容易得出结论，开桶统计1的个数，聚集的放入数中

 1 import math
 2 n=int(input())
 3 a=[int(i)for i in input().split()]
 4 su=sum(a)
 5 x=[0]*20
 6 for i in a:
 7     for j in range(16):
 8         x[j]+=(i>>j)&1
 9 l=[]
10 for i in a:
11     tmp=0
12     for j in range(16):
13         if(x[j]!=0):
14             tmp+=(1<<j)
15             x[j]-=1
16     l.append(tmp)
17 up=0
18 for i in l:
19     up+=(i*n-su)**2
20 gcd=math.gcd(up,n**3)
21 print("{}/{}".format(str(up//gcd),str(n**3//gcd)))

https://ac.nowcoder.com/acm/contest/33189/K

题意：从0开始，往后补数使%n= 1,2,3,...,n，求数长度min

直接模拟，交Pypy（居然）比Python快很多

 1 n = int(input())
 2 ans = 0
 3 for i in range(1,n+1):
 4     k = 1
 5     while(1):
 6         tens = 10**k
 7         x = (i - (i-1)*tens) % n
 8         if(x < tens):
 9             ans += k
10             break
11         k +=1
12 if(n==1):
13     ans = 0
14 print(ans)

https://ac.nowcoder.com/acm/contest/33190/G

回文问题，求以k，f，c结尾的回文串数量，板子题，挖坑回头补

 1 #define _CRT_SECURE_NO_WARNINGS
 2 #include<bits/stdc++.h>
 3 using namespace std;
 4 #define int long long
 5 const int maxn = 2e6 + 5;
 6 char s[maxn];
 7 int a[maxn];
 8 int trans[maxn][26], fail[maxn], len[maxn], dep[maxn], cnt = 1, cur;
 9 signed main(){
10     ios::sync_with_stdio(false); cin.tie(0), cout.tie(0);
11     int nn; cin >> nn >> s;
12     fail[0] = 1, fail[1] = 0, len[0] = 0, len[1] = -1;
13     int n = strlen(s + 1);
14     long long ak = 0, af = 0, ac = 0;
15     for (int i = 1; i <= n; ++i){
16         a[i] = (s[i] - 'a');
17         int C = 0;
18         while (i - len[cur] - 1 <= 0 || a[i - len[cur] - 1] != a[i]) cur = fail[cur];
19         if (!trans[cur][a[i]]){
20             int t = fail[cur];
21             while (i - len[t] - 1 <= 0 || a[i - len[t] - 1] != a[i]) t = fail[t];
22             fail[++cnt] = trans[t][a[i]],
23                 dep[cnt] = dep[fail[cnt]] + 1,
24                 trans[cur][a[i]] = cnt,
25                 len[cnt] = len[cur] + 2;
26         }
27         cur = trans[cur][a[i]];
28         if (s[i] == 'k') ak += dep[cur];
29         else if (s[i] == 'f') af += dep[cur];
30         else if (s[i] == 'c') ac += dep[cur];
31     }
32     cout << ak << " " << af << " " << ac << endl;
33     return 0;
34 }

https://ac.nowcoder.com/acm/contest/33190/H

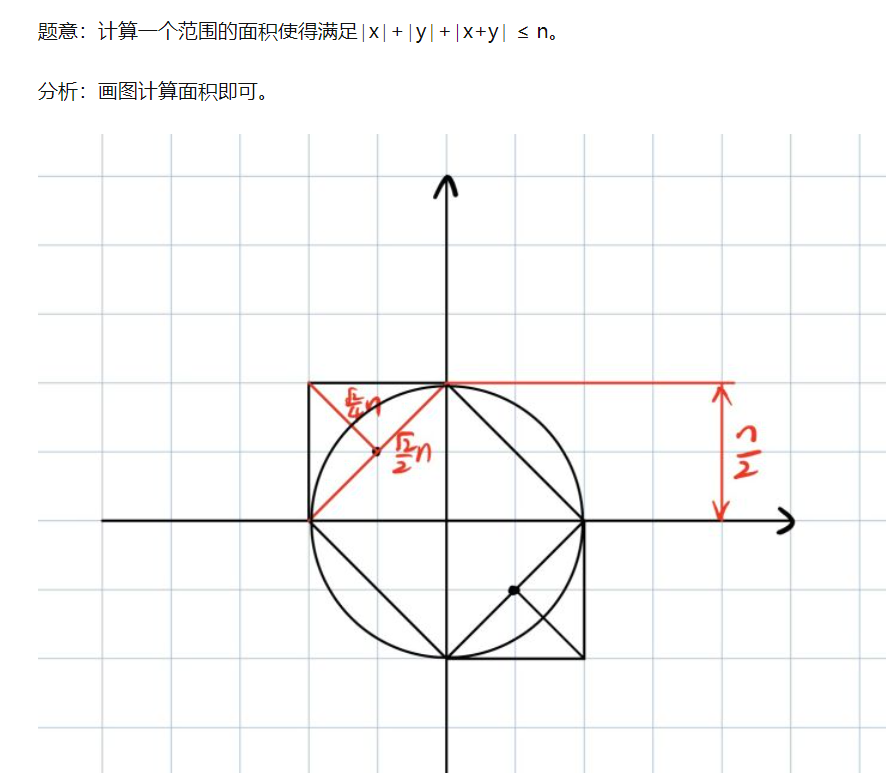
1 import math 
2 d=int(input())/2
3 s=d**2*2+0.5*math.pi*d**2
4 print(s)

https://ac.nowcoder.com/acm/contest/33190/F

计算几何，我的最爱

 1 #define _CRT_SECURE_NO_WARNINGS
 2 #include <bits/stdc++.h>
 3 #define int long long
 4 using namespace std;
 5 const double pi = acos(-1.0);
 6 struct rec {
 7     double l, r;
 8 }p[2050];
 9 double x[1050], y[1050], r[1050]; int n;
10 bool cmp(rec a, rec b) { return a.l < b.l || (a.l == b.l && a.r > b.r); }
11 double dis(int a, int b) { return sqrt(1.0 * (x[a] - x[b]) * (x[a] - x[b]) + 1.0 * (y[a] - y[b]) * (y[a] - y[b])); }
12 double ans;
13 void solve(int i) {
14     int cnt = 0;
15     for (int j = i + 1; j <= n; j++) {
16         double d = dis(i, j);
17         if (r[i] + d <= r[j])
18             return;
19         if (d <= r[i] + r[j] && !(r[j] + d <= r[i])) {
20             double ang1 = atan2((y[j] - y[i]), (x[j] - x[i]));
21             double ang2 = acos((d * d + r[i] * 1.0 * r[i] - r[j] * 1.0 * r[j]) / (2 * d * r[i]));
22             double L = ((ang1 - ang2) < 0) ? ang1 - ang2 + 2 * pi : ang1 - ang2;
23             double R = ((ang1 + ang2) < 0) ? ang1 + ang2 + 2 * pi : ang1 + ang2;
24             if (L > R) {
25                 p[++cnt].l = 0;
26                 p[cnt].r = R;
27                 p[++cnt].l = L;
28                 p[cnt].r = 2 * pi;
29             }
30             else {
31                 p[++cnt].l = L;
32                 p[cnt].r = R;
33             }
34         }
35     }
36     sort(p + 1, p + cnt + 1, cmp);
37     double lim = 0, sum = 0;
38     for (int j = 1; j <= cnt; j++) {
39         if (p[j].l > lim)
40             sum += p[j].l - lim;
41         lim = max(p[j].r, lim);
42     }
43     sum += 2 * pi - lim;
44     ans += sum * r[i];
45 }
46 signed main() {
47     ios::sync_with_stdio(false); cin.tie(0), cout.tie(0);
48     while (cin >> n) {
49         ans = 0;
50         for (int i = 1; i <= n; i++) cin >> x[i] >> y[i] >> r[i];
51         for (int i = 1; i <= n; i++) solve(i);
52         cout << setprecision(10) << ans << endl;
53     }
54 }

https://atcoder.jp/contests/abc127/tasks/abc127_e

排列组合，喜欢这个namespace binomial，抄过来嘿嘿嘿

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define int long long
 4 const int mod = 1e9 + 7;
 5 namespace binomial {
 6     const int mmm = 2e6 + 9;
 7     int fac[mmm], ivf[mmm];
 8     int qpow(int x, int n, int c = 1) {
 9         for (; n; n /= 2, x = x * x % mod) if (n & 1)c = c * x % mod;
10         return c;
11     }
12     void init() {
13         fac[0] = 1;
14         for (int i = 1; i < mmm; i++) fac[i] = fac[i - 1] * i % mod;
15         ivf[mmm - 1] = qpow(fac[mmm - 1], mod - 2);
16         for (int i = mmm - 1; i > 0; i--) ivf[i - 1] = ivf[i] * i % mod;
17     }
18     int C(int n, int m) {
19         if (!fac[0]) init();
20         if (n < 0 || m < 0 || n < m) return 0;
21         return fac[n] * ivf[m] % mod * ivf[n - m] % mod;
22     }
23     int catalan(int n) { return C(2 * n, n) - C(2 * n, n - 1); }
24 }
25 vector<int>rm(1e6 + 7);
26 using namespace  binomial;
27 signed main() {
28     ios::sync_with_stdio(false); cin.tie(0), cout.tie(0);
29     int n, m, k; cin >> n >> m >> k;
30     for (int i = 1; i <= 1e6; i++) {
31         rm[i] = rm[i - 1] + (i * (i + 1)) / 2 % mod;
32         rm[i] %= mod;
33     }
34     int tmp = C(n * m - 2, k - 2);
35     int tmp2 = rm[n - 1] * (m) % mod * (m) % mod + rm[m - 1] * (n) % mod * (n) % mod;
36     tmp2 %= mod;
37     int tmp3 = (tmp2 * tmp) % mod;
38     cout << tmp3 << "\n";
39     return 0;
40 }

https://atcoder.jp/contests/arc102/tasks/arc102_b

题意：构造一种有向图，起点终点有且只有L条长度为0~(L-1)的路径

思路，二进制构造，点只有20个刚好差一位，很难受，但是边多给了(60 - 40)条，所以怎么用边换点补一位是关键

前面的不同的点已经构造了唯一的路径，第ai个代表第ai位的点可以构造出pow(2, x)以内的所有路径

从ai点出发向终点连边权重k，即可构造(k, k + pow(2, ai))的唯一路径

所以利用前19位的点向终点连边，20*2+20 = 60条边可以构造2**(20 - 1) * 2的路径

很好的构造题，其实也没有那么难想，只是生疏了，而且把榜带歪了

 1 #define _CRT_SECURE_NO_WARNINGS
 2 #include <bits/stdc++.h>
 3 using namespace std;
 4 #define int long long
 5 int L, n = 20;
 6 struct Edge {
 7     int x, y, v;
 8 }e[66]; 
 9 int E, V;
10 inline void add(int u, int v, int w) {
11     e[++E] = {u,v,w};
12 }
13 signed main() {
14     ios::sync_with_stdio(false); cin.tie(0), cout.tie(0);
15     cin >> L; int tmp = L;
16     while (tmp) ++V, tmp >>= 1;
17     for (int i = 1; i < V; i++) {
18         add(i, i + 1, 0);
19         add(i, i + 1, 1 << (V - i - 1));
20     }
21     int now = 1 << (V - 1);
22     for (int i = V - 1; i >= 1; i--) {
23         if (L & (1 << (i - 1))) {
24             add(1, V - i + 1, now);
25             now += 1 << (i - 1);
26         }
27     }
28     cout << V << " " << E << "\n";
29     for (int i = 1; i <= E; i++)
30         cout << e[i].x << " " << e[i].y << " " << e[i].v << "\n";
31     return 0;
32 }

https://atcoder.jp/contests/abc263/tasks/abc263_e

题意：n个格子都有骰子，分别ai个面，走到哪扔哪个骰子，扔骰子到终点的步数期望

期望DP，注意最终概率和为1，倒推

 1 #define _CRT_SECURE_NO_WarrRNINGS 1
 2 #include <bits/stdc++.h>
 3 #define int long long
 4 using namespace std;
 5 const int mod = 998244353;
 6 const int maxn = 3e5 + 5;
 7 int arr[maxn], suf[maxn], dp[maxn];
 8 
 9 int qpow(int x, int y) {
10     int res = 1;
11     while (y) {
12         if (y & 1) res = res * x % mod;
13         x = x * x % mod;
14         y >>= 1;
15     }
16     return res;
17 }
18 
19 
20 signed main() {
21     ios::sync_with_stdio(false); cin.tie(0), cout.tie(0);
22     int n; cin >> n;
23     for (int i = 1; i <= n - 1; i++) cin >> arr[i];
24 
25     for (int i = n - 1; i; i--) {
26         int pos = ((suf[i + 1] - suf[i + arr[i] + 1] + arr[i] + 1) % mod + mod) % mod;
27         dp[i] = pos * qpow(arr[i], mod - 2) % mod;
28         suf[i] = (suf[i + 1] + dp[i]) % mod;
29     }
30 
31     cout << dp[1] << endl;
32 
33     return 0;
34 }

https://ac.nowcoder.com/acm/contest/33192/C

题意：给定数组A，构造排列P使Pi != Ai

由于排列没有重复，因此碰到相同的数直接用排列的另一个数即可，这样可以轻易排好n-1个数，关键在最后一个数

最后一个数如果相同，遍历前面的n-1个数，若某数交换成立，交换即可

写法看似O(n**2)，实际O(2*n)

 1 for _ in range(int(input())):
 2     n = int(input())
 3     a = list(map(int,input().split()))
 4     ans=[i for i in range(1,n+1)]
 5     l = set(a)
 6     if len(l)==1:
 7         print("NO")
 8         continue
 9     for i in range(n):
10         if a[i] != ans[i]:
11             continue
12         for j in range(n):
13             if a[i]!=ans[j] and a[j]!=ans[i]:
14                 ans[j],ans[i]=ans[i],ans[j]
15     print("YES")
16     print(*ans)

https://ac.nowcoder.com/acm/contest/33192/F

题意：n长环形数组，相邻数如果值相同或和为x可删，最多删几次

注意和为 n 可以把其中一个数当作 x-n，先把所有大于 x/2 的 ai 转化(x - ai)这样就转化为了消除相邻相同数

 1 #define _CRT_SECURE_maxnO_WARmaxnImaxnG
 2 #include <bits/stdc++.h>
 3 #define int long long
 4 using namespace std;
 5 const int maxn = 2e6 + 5;
 6 int a[maxn], stk[maxn], top;
 7 
 8 signed main(){
 9     ios::sync_with_stdio(false); cin.tie(0), cout.tie(0);
10     int n, m;  cin >> n >> m;
11     for (int i = 1; i <= n; i++) cin >> a[i];
12     int cnt = 0;
13     for (int i = 1; i <= n; i++){
14         if (!top) stk[++top] = a[i];
15         else if (stk[top] + a[i] == m) top--, cnt++;
16         else if (stk[top] == a[i]) top--, cnt++;
17         else stk[++top] = a[i];
18     }
19     for (int i = 1; i <= top / 2; i++){
20         if (stk[i] == stk[top - i + 1]) cnt++;
21         else if (stk[i] + stk[top - i + 1] == m) cnt++;
22         else break;
23     }
24     cout << cnt << endl;
25 }

https://ac.nowcoder.com/acm/contest/33191/J

题意：两种操作，问 C 能不能变成 x

1. Change B to A-B. 2. Change C to B-C.

注意到操作1做偶数次等于0次，操作2同理

一次操作1接一次操作2可以有效改变C，把C变成C+(a - 2 * b)

特判a = 2 * b即可

1 T=int(input())
2 for i in range(T):
3     A,B,C,x=map(int,input().split())
4     if A==2*B:
5         print('Yes' if C==x or x+C==B else 'No')
6     else:
7         print('Yes' if (x-C)%(2*B-A)==0 or (x+C-B)%(2*B-A)==0 else 'No')

https://ac.nowcoder.com/acm/contest/33191/B

思路1比较显然，思路2(1)没想到，改天补一下树链剖分的内容，思路2(2)也没想到，我有问题

思路2(3)树上倍增再二分比较好想，不过带log，不愧是大常数队伍

这份题解板子写的好像不错(因为我没有树链板子)，于是就抄过来了doge

  1 #define _CRT_SECURE_NO_WARNINGS
  2 #include <bits/stdc++.h>
  3 //#define int long long
  4 using namespace std;
  5 const int maxn = 2e6 + 5;
  6 
  7 //存图模板
  8 struct Graph {
  9     struct edge { int Next, to; };
 10     edge G[maxn << 1];
 11     int head[maxn];
 12     int cnt;
 13     Graph() :cnt(2) {}
 14     void clear(int n) {
 15         cnt = 2; fill(head, head + n + 2, 0);
 16     }
 17     void add_edge(int u, int v) {
 18         G[cnt].to = v;
 19         G[cnt].Next = head[u];
 20         head[u] = cnt++;
 21     }
 22 };
 23 Graph G;
 24 int N, M;
 25 
 26 //长链剖分模板
 27 int Deep[maxn], Height[maxn], Anc[maxn][20], Top[maxn], Hson[maxn];
 28 int highbit[maxn], MaxDeep[maxn];
 29 vector<int> Up[maxn], Down[maxn], Path;
 30 void DFS1(int u, int fa) {
 31     Anc[u][0] = fa;
 32     Height[u] = 1;
 33     for (int i = 1; i < 20; ++i)
 34         Anc[u][i] = Anc[Anc[u][i - 1]][i - 1];
 35     for (int i = G.head[u]; i; i = G.G[i].Next) {
 36         int v = G.G[i].to;
 37         if (v == fa) continue;
 38         Deep[v] = Deep[u] + 1;
 39         DFS1(v, u);
 40         Height[u] = max(Height[u], Height[v] + 1);
 41         if (Height[Hson[u]] < Height[v]) Hson[u] = v;
 42     }
 43     return;
 44 }
 45 void DFS2(int u, int fa, int top) {
 46     Path.push_back(u);
 47     Top[u] = top;
 48     MaxDeep[top] = max(MaxDeep[top], Deep[u]);
 49     Down[top].push_back(u);
 50     if (Hson[u]) DFS2(Hson[u], u, top);
 51     for (int i = G.head[u]; i; i = G.G[i].Next) {
 52         int v = G.G[i].to;
 53         if (v == fa || v == Hson[u]) continue;
 54         DFS2(v, u, v);
 55     }
 56     if (u == top) {
 57         int len = MaxDeep[top] - Deep[u] + 1;
 58         for (int i = Path.size() - 1; i >= max((int)Path.size() - len - 1, 0); --i)
 59             Up[top].push_back(Path[i]);
 60     }
 61     Path.pop_back();
 62 }
 63 int KthAnc(int u, int k) {  //求u的k级祖先
 64     if (k > Deep[u]) return 0;
 65     if (k == 0) return u;
 66     u = Anc[u][highbit[k]];
 67     k -= (1 << highbit[k]);
 68     if (Deep[u] - k == Deep[Top[u]]) return Top[u];
 69     if (Deep[u] - k > Deep[Top[u]]) return Down[Top[u]][Deep[u] - k - Deep[Top[u]]];
 70     return Up[Top[u]][Deep[Top[u]] - (Deep[u] - k)];
 71 }
 72 
 73 
 74 //对树上差分求前缀和
 75 int v[maxn];
 76 int s[maxn], ans[maxn];
 77 int dfs(int u, int f) {
 78     for (int i = G.head[u]; i; i = G.G[i].Next) {
 79         int v = G.G[i].to;
 80         if (v == f) continue;
 81         dfs(v, u);
 82         ans[u] += ans[v];
 83     }
 84     ans[u] += s[u];
 85     return ans[u];
 86 }
 87 
 88 signed main() {
 89     ios::sync_with_stdio(false); cin.tie(0), cout.tie(0);
 90     cin >> N;
 91     for (int i = 1; i <= N - 1; ++i) {
 92         int u, v; cin >> u >> v;
 93         G.add_edge(u, v);
 94         G.add_edge(v, u);
 95     }
 96     DFS1(1, 0);
 97     DFS2(1, 0, 1);
 98     int Max = 1;
 99     for (int i = 1; i <= N; ++i) {
100         if ((i >> Max) & 1) ++Max;
101         highbit[i] = Max - 1;
102     }
103     for (int i = 1; i <= N; i++) {
104         ans[i] = 0;  s[i] = 1; //每个点都会被+1，所以直接初始值+1
105     }
106     for (int i = 1; i <= N; i++) {
107         cin >> v[i];
108         int lst = KthAnc(i, v[i] + 1);  //第i个点的k+1级祖先
109         s[lst]--;
110     }
111     dfs(1, -1);
112     for (int i = 1; i <= N; i++) cout << ans[i] << " ";
113     cout << "\n";
114     return 0;
115 }

posted on 2022-09-28 17:08 Yukino酱～阅读(34) 评论(0) 收藏举报

刷新页面返回顶部