BOI2020 DAY2
BOI2020 DAY2
前言
BOI还是原来的味道。。好难。。但是看到好多人当场AK了。。果然是我太菜了吗。。
A Graph
题意
一个\(n\)个点\(m\)条边的无向图,每条边有一个权值\(c(c=1,2)\) ,要求给每个点分配一个实数,使每条边上的两点的值之和等于边的权值。\(1\leq n\leq 100000\) ,\(1\leq m\leq 200000\)。
题解
还是比较好想的,先把一个点设为\(x\) ,然后用关于x的式子表示同一联通块的点,然后出现环的时候就是就会有方程。容易看出式子和方程都是一次的。如果出现方程,那么\(x\)是定值;若无方程,就是若干个\(|x+b|\)形式的式子之和求最小值。要注意可能不止一个联通块以及答案最多只有一位小数。
\(Code\)
#include<bits/stdc++.h>
#define LL long long
#define ull unsigned long long
#define LL long long
using namespace std;
const int N=2e5+10;
const int M=3e5+10;
int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
void print(LL x){
if(x>9) print(x/10);
putchar(x%10+'0');
}
int n,m,cnt=1;
struct edge{
int r,nxt;
int c;
}e[M<<1];
int a[N],b[N];
double ans[N],X;
int vis[N],vis2[N],hed[N];
bool f,youjie;
void insert(int u,int v,int c){
e[++cnt].r=v;e[cnt].c=c;e[cnt].nxt=hed[u];hed[u]=cnt;
}
void J(int A,int B,int c){
c=c-B;
if((!A)&&(!c)) return;
if(!A) {youjie=0;return;}
double y=(double)c/(double)A;
if((!f)||y==X) {X=y;f=1;return;}
youjie=0;return;
}
int q[N];int top;
void dfs(int u){
int v;
for(int i=hed[u];i&&youjie;i=e[i].nxt){
v=e[i].r;
if(!vis[v]){
vis[v]=1;
a[v]=-a[u];
b[v]=e[i].c-b[u];
q[++top]=-a[v]*b[v];
dfs(v);
}
else{
J(a[u]+a[v],b[u]+b[v],e[i].c);
}
}
}
void getans(int u){
ans[u]=(double)a[u]*X+(double)b[u];
for(int i=hed[u];i;i=e[i].nxt)
if(!vis2[e[i].r]) {
vis2[e[i].r]=1;
getans(e[i].r);
}
}
int main(){
int u,v,c;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i){
scanf("%d%d%d",&u,&v,&c);
insert(u,v,c);insert(v,u,c);
}
bool flag=1;
for(int i=1;i<=n;++i){
if(vis[i]) continue;
a[i]=1;b[i]=0;f=0;youjie=1;vis[i]=1;top=1;q[1]=0;
dfs(i);
if(!youjie) {
flag=0;
break;
}
if(!f){
sort(q+1,q+1+top);
X=q[(top+1)/2];
}
vis2[i]=1;
getans(i);
}
if(!flag) printf("NO\n");
else {
printf("YES\n");
for(int i=1;i<=n;++i) cout<<ans[i]<<" ";
puts("");
}
return 0;
}
B1 Village
题意
一棵\(n\)个点的树,树上的每条边的长度都是\(1\) 。每个点上有一个居民,现在每个居民都要搬到其他点上,每个点上最多有一个居民。假设原来在\(i\)的居民搬到点\(p_i(i\neq p_i)\) ,则这个居民经过距离为\(i\)到\(p_i\)的距离。要求每个居民经过的距离总和最小并给出方案。\(1\leq n \leq 100000\)
题解
要让每个居民移动次数尽量少,直接贪心让每个与当前编号相等的点与其父亲交换即可。
\(Code\)
#include<bits/stdc++.h>
#define LL long long
#define ull unsigned long long
#define LL long long
using namespace std;
const int N=3e5+10;
int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
void print(LL x){
if(x>9) print(x/10);
putchar(x%10+'0');
}
int n,cnt=1;
struct edge{
int r,nxt;
}e[N];
int hed[N];
void insert(int u,int v){
e[++cnt].r=v;e[cnt].nxt=hed[u];hed[u]=cnt;
}
LL ans=0;
int p[N],fa[N];
void dfs(int u){
for(int i=hed[u];i;i=e[i].nxt){
if(e[i].r==fa[u])continue;
fa[e[i].r]=u;
dfs(e[i].r);
}
if(p[u]==u&&fa[u]){
ans+=2;
swap(p[u],p[fa[u]]);
}
}
int main(){
int u,v;
scanf("%d",&n);
for(int i=1;i<n;++i){
scanf("%d%d",&u,&v);
insert(u,v);insert(v,u);
}
for(int i=1;i<=n;++i) p[i]=i;
dfs(1);
if(p[1]==1) {
v=e[hed[1]].r;
ans+=2;
swap(p[1],p[v]);
}
printf("%I64d\n",ans);
for(int i=1;i<=n;++i) printf("%d ",p[i]);puts("");
return 0;
}
B2 Village
题意
一棵\(n\)个点的树,树上的每条边的长度都是\(1\) 。每个点上有一个居民,现在每个居民都要搬到其他点上,每个点上最多有一个居民。假设原来在\(i\)的居民搬到点\(p_i(i\neq p_i)\) ,则这个居民经过距离为\(i\)到\(p_i\)的距离。要求每个居民经过的距离总和最大。\(1\leq n \leq 100000\)
题解
题面和B1是一样的,但现在要求最大值。对于一条边\(E(u,v)\) ,一棵树被分成两边,那么答案最大时应该要满足这条边两侧的点尽量多的通过这条边。那么一条边对答案的贡献就是点数较小的一侧的点数\(\times 2\) ,可以证明答案是可以达到的。
然后是方案。如果一颗子树的点数大于一半就会很难处理,所以考虑先找出重心作为新根。这样之后,一条边的点数较少一侧一定是其所连的子树。在凑方案时一颗子树内的居民显然不能留在这可子树里,但子树外的其他点都可以搬去。于是问题就变成一个轮换的问题,按套路来就行了。
\(Code\)
#include<bits/stdc++.h>
#define LL long long
#define ull unsigned long long
#define LL long long
using namespace std;
const int N=3e5+10;
int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
void print(LL x){
if(x>9) print(x/10);
putchar(x%10+'0');
}
int n,cnt=1,rt;
struct edge{
int r,nxt;
}e[N];
int hed[N];
void insert(int u,int v){
e[++cnt].r=v;e[cnt].nxt=hed[u];hed[u]=cnt;
}
bool vis[N];
int siz[N],son[N];
LL ans=0;
void dfs(int u){
vis[u]=1;siz[u]=1;
for(int i=hed[u];i;i=e[i].nxt){
if(vis[e[i].r]) continue;
dfs(e[i].r);
siz[u]+=siz[e[i].r];
if(siz[e[i].r]>siz[son[u]]) son[u]=e[i].r;
}
}
int fa[N];
void getans(int u){
siz[u]=1;
for(int i=hed[u];i;i=e[i].nxt)
if(fa[u]!=e[i].r){
fa[e[i].r]=u;
getans(e[i].r);
siz[u]+=siz[e[i].r];
if(siz[e[i].r]>siz[son[u]]) son[u]=e[i].r;
ans=ans+(LL)2*(LL)min(siz[e[i].r],n-siz[e[i].r]);
}
}
vector<int> ve;
bool cmp(int A,int B){return siz[A]>siz[B];}
int t1=0,t2=0;
int p1[N],p2[N],p[N];
void dfs2(int u,int *p,int &top){
p[++top]=u;
for(int i=hed[u];i;i=e[i].nxt)
if(fa[u]!=e[i].r) dfs2(e[i].r,p,top);
}
int main(){
int u,v;
scanf("%d",&n);
for(int i=1;i<n;++i){
scanf("%d%d",&u,&v);
insert(u,v);insert(v,u);
}
dfs(1);
for(int i=1;i<=n;++i){
u=max(siz[son[i]],n-siz[i]);
if(u<=(n/2)) {rt=i;break;}
}
memset(siz,0,sizeof(siz));
memset(son,0,sizeof(son));
getans(rt);
printf("%I64d\n",ans);
for(int i=hed[rt];i;i=e[i].nxt) ve.push_back(e[i].r);
sort(ve.begin(),ve.end(),cmp);
for(int i=0;i<ve.size();++i) dfs2(ve[i],p1,t1);
p1[++t1]=rt;
for(int i=1;i<ve.size();++i) dfs2(ve[i],p2,t2);
p2[++t2]=rt;dfs2(ve[0],p2,t2);
for(int i=1;i<=t1;++i) p[p1[i]]=p2[i];
for(int i=1;i<=n;++i) printf("%d ",p[i]);puts("");
return 0;
}
C Viruses
题意
给定一种病毒,为了方便,我们用 \(0\) 到 \(G-1\) 的整数描述他的基因序列。
现在这个病毒可以进行变异,已知变异规则,每个变异规则可以让基因序列上的某个数变成某个片段,如果用变异规则让基因序列变成了全部为 \(0\) 和 \(1\) 的序列,那么这个病毒就变异完成了。
例子:
假设给出的如下图:
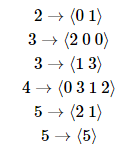
那么可能的变化如下:

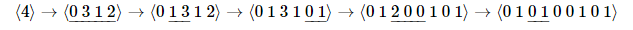
病毒可以通过抗体进行检测,比如 \(01011\) 就可以检测到 \(0101110\) ,但不能检测到 \(110110\) 。
对于从 \(2\) 到 \(G-1\) 中的基因,科学家想知道,是否能通过任意一组给定的抗体检测到这个基因变异形成的其他所有基因,不能的话,那么求不能检测到的基因中的最短长度。
输入格式:
第一行三个整数 \(G,N,M\) 代表基因数,变异规则数和抗体数。
接下来 \(N\) 行每行首先两个整数 \(a,k\) ,然后接着 \(k\) 个整数 \(b_i\) ,代表 \(a\) 可以通过这个变异规则变为 \(b_1,b_2,\cdots,b_k\) 这个片段,保证 \(2\) 和 \(G-1\) 都至少在每个规则中的 \(a\) 中出现一次。
接下来 \(M\) 行每行首先一个整数 \(l\) 代表抗体长度,接下来 \(l\) 个整数 \(c_i\) 描述这个抗体。
\(G>2\) , \(N\geq G-2\) , \(M\geq 0\) , \(2\leq a<G\) , \(k\geq 1\) , \(0\geq b_i<G\) , \(l>0\) , \(0\leq c_i\leq 1\) , \(\sum{k}\leq 100\) , \(\sum{l}\leq 50\) 。
输出格式
\(G-2\) 行第 \(i\) 行代表 \(i\) 基因以及其所有变异到的基因是否都可以被任意一组抗体检测到,如果可以,输出一个字符串 \(YES\),如果不可以,首先一个字符串 \(NO\),接下来一个整数代表不能检测到的基因中的最短长度。
题解
变量是真的多。。。我tm人都看晕了。。看了题解之后才弄清。。。
先考虑 \(M=0\) 的情况。这个时候不需要考虑抗体的问题,只需要算出每种基因最后能产生的最短的病毒。这个用类似最短路的做法就可以。令\(dp_i\)为由基因\(i\)能产生的最短病毒,显然\(dp_0=dp_1=1\)。每次用所有的“规则”进行转移,如果已经没有能够转移的状态或已经转移过 \(G-2\) 轮就停下来。由于每个数据的范围都很小,复杂度肯定是够的。
然后考虑 \(M=1\) 的情况。抗体只有一个,但已经可能出现某些病毒被抗体匹配掉的情况。考虑我们用某一个“规则” \(a_i(b_1,b_2...b_{k_i})\) 进行转移时,任何一个\(b_j\) 显然都不应该能被抗体匹配掉,否则整体就会被匹配,然后就是由若干个 \(b_j\) 拼接后的接口处不该被抗体匹配掉。\(b_j\) 是否会被匹配掉可以通过 \(dp_i\) 体现出来,但拼接的情况不好处理,因为串的长度在多次变化后可能会非常大,直接储存是肯定不行的。考虑到抗体不长,我们只需能够储存串两端状态即可。
扩展我们的dp方式,令 \(dp_{i,st,ed}\) 表示通过基因 \(i\) 使得状态从 \(st\) 变化到 \(ed\) 产生的病毒的最短长度。由于只有一个抗体,我们认为 \(st\) 和 \(ed\) 状态都可以用其末端在抗体上从左到右能匹配的最长长度来表示。这种状态的表达方式可能令人熟悉。。。嗯。。就是KMP啦。。当然,我们需要提前处理出每个状态后接 \(0\) 或 \(1\) 走到的状态,然后用这些状态进行像 \(M=0\) 情况下的类似最短路的转移。代码如下。
\(Code(M=1)\)
#include<bits/stdc++.h>
#define LL long long
#define ull unsigned long long
using namespace std;
const int N=103;
const int S=53;
const ull INF = -1;
int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
void print(LL x){
if(x>9) print(x/10);
putchar(x%10+'0');
}
int G,n,m;
int a[N],k[N],b[N][N];
int l[S],c[S][S];
ull dp[N][S][S];
ull tp[S][S];
int cnt;
int nxt[S],go[S][2];
void KMP(int len,int *s){
int j=0;
for(int i=2;i<=len;++i){
while(j>0&&s[j+1]!=s[i]) j=nxt[j];
if(s[j+1]==s[i]) ++j;
nxt[i]=j;
}
go[len][0]=go[len][1]=len;
for(int i=0;i<len;++i){
for(int h=0;h<=1;++h){
if(h==s[i+1]) go[i][h]=i+1;
else go[i][h]=go[nxt[i]][h];
}
}
}
bool sol(int row){
bool re=0;
for(int st=0;st<=cnt;++st){
fill_n(tp[0],S*S,INF);
tp[0][st]=0;
for(int it=1;it<=k[row];++it){
int h=b[row][it];
for(int i=0;i<=cnt;++i){
if(tp[it-1][i]>=INF)
continue;
for(int j=0;j<=cnt;++j)
if(dp[h][i][j]<INF)
tp[it][j]=min(tp[it][j],tp[it-1][i]+dp[h][i][j]);
}
}
for(int ed=0;ed<=cnt;++ed){
if(dp[a[row]][st][ed]>tp[k[row]][ed]){
dp[a[row]][st][ed]=tp[k[row]][ed];
re=1;
}
}
}
return re;
}
int main(){
scanf("%d%d%d",&G,&n,&m);
for(int i=1;i<=n;++i){
scanf("%d%d",&a[i],&k[i]);
for(int j=1;j<=k[i];++j){
scanf("%d",&b[i][j]);
}
}
for(int i=1;i<=m;++i){
scanf("%d",&l[i]);
for(int j=1;j<=l[i];++j){
scanf("%d",&c[i][j]);
}
}
KMP(l[1],c[1]);
cnt=l[1];
fill_n(dp[0][0],N*S*S,INF);
for(int i=0;i<=cnt;++i){
for(int h=0;h<=1;++h){
dp[h][i][go[i][h]]=1;
}
}
int flag=1,it=0;
for(;flag&&it<G-2;++it){
flag=0;
for(int i=1;i<=n;++i) flag|=sol(i);
}
for(int i=2;i<G;++i) {
ull ans=INF;
for(int j=0;j<cnt;++j)
ans=min(ans,dp[i][0][j]);
if(ans<INF) cout<<"NO " <<ans<<endl;
else cout<<"YES"<<endl;
}
return 0;
}
现在仅仅是解决了 \(M=1\) 的情况。接下来考虑没有限制的情况。\(M>1\) 之后,需要处理的问题更加复杂。dp的方式全都不变,现在考虑 \(st\) 和 \(ed\) 怎么表达,我们会发现上面再处理每种状态的后继状态的问题正是AC自动机所解决的问题。而且AC自动机恰好是KMP的上位替代。直接用AC自动机上的各节点代表 \(st\) 和 \(ed\) 等状态,dp的转移方式和之前是一样的。最差情况下的效率\(O(G\cdot (\sum{k}) \cdot (\sum{l})^3)\),已经可以通过。这里使用类似floyd的方法进行转移,所以复杂度较高。其实可以每次只取已知的已有最短的病毒的那种基因来进行转移,这样的话会比较类似dijkstra,效率可以到优化原题解的 \(O(G\cdot (\sum{l})^3 \cdot log(G \cdot (\sum{l})^2))\) 。
\(Code\)
#include<bits/stdc++.h>
#define LL long long
#define ull unsigned long long
using namespace std;
const int N=103;
const int S=55;
const ull INF = -1;
int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
void print(LL x){
if(x>9) print(x/10);
putchar(x%10+'0');
}
int G,n,m;
int a[N],k[N],b[N][N];
int l[S],c[S][S];
ull dp[N][S][S];
ull tp[S][S];
int cnt;
queue<int>q;
struct ACauto{
int t[S][2],val[S],fail[S];
void ins(int len,int *s){
int now=0;
for(int i=1;i<=len;i++){
int v=s[i];
if(!t[now][v]) t[now][v]=++cnt;
now=t[now][v];
}
val[now]++;
}
void build(){
for(int i=0;i<2;i++)
if(t[0][i]) {
fail[t[0][i]]=0;
q.push(t[0][i]);
}
while(!q.empty()){
int u=q.front();q.pop();
for(int i=0;i<2;i++) {
if(t[u][i]) {
fail[t[u][i]]=t[fail[u]][i];
q.push(t[u][i]);
}
else t[u][i]=t[fail[u]][i];
}
}
for(int j=0;j<=cnt;++j){
int flag=val[j],i=j;
while(i){
i=fail[i];
flag=max(flag,val[i]);
}
val[j]=flag;
if(val[j]) t[j][0]=t[j][1]=j;
}
}
}AC;
bool sol(int row){
bool re=0;
for(int st=0;st<=cnt;++st){
fill_n(tp[0],S*S,INF);
tp[0][st]=0;
for(int it=1;it<=k[row];++it){
int h=b[row][it];
for(int i=0;i<=cnt;++i){
if(tp[it-1][i]>=INF)
continue;
for(int j=0;j<=cnt;++j)
if(dp[h][i][j]<INF)
tp[it][j]=min(tp[it][j],tp[it-1][i]+dp[h][i][j]);
}
}
for(int ed=0;ed<=cnt;++ed){
if(dp[a[row]][st][ed]>tp[k[row]][ed]){
dp[a[row]][st][ed]=tp[k[row]][ed];
re=1;
}
}
}
return re;
}
int main(){
scanf("%d%d%d",&G,&n,&m);
for(int i=1;i<=n;++i){
scanf("%d%d",&a[i],&k[i]);
for(int j=1;j<=k[i];++j){
scanf("%d",&b[i][j]);
}
}
for(int i=1;i<=m;++i){
scanf("%d",&l[i]);
for(int j=1;j<=l[i];++j){
scanf("%d",&c[i][j]);
}
AC.ins(l[i],c[i]);
}
AC.build();
fill_n(dp[0][0],N*S*S,INF);
for(int i=0;i<=cnt;++i){
for(int h=0;h<2;++h){
dp[h][i][AC.t[i][h]]=1;
}
}
int flag=1,it=0;
for(;flag&&it<G-2;++it){
flag=0;
for(int i=1;i<=n;++i) flag|=sol(i);
}
for(int i=2;i<G;++i) {
ull ans=INF;
for(int j=0;j<=cnt;++j)
if(!AC.val[j]){
ans=min(ans,dp[i][0][j]);
}
if(ans<INF) cout<<"NO " <<ans<<endl;
else cout<<"YES"<<endl;
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号