多层神经网络反向传播推导过程小结
先看一下多层神经网络的结构图:
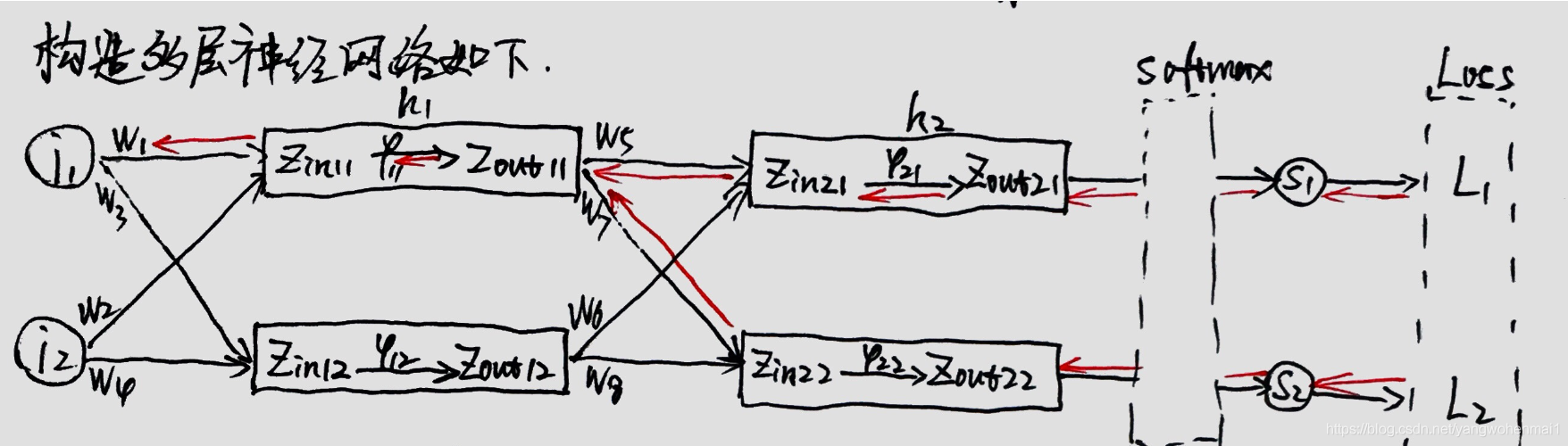
举个例子,图中的h1和h2代表两个网络层,在h1和h2层中各有一个激活函数,分别是φ11和φ21。
1.输入数据i1与权重W相乘,得Zin11,Zin11通过激活函数φ11得到Zout11.
2.Zout11继续与权重W相乘,得到Zin21,Zin21通过激活函数φ21得到Zout21.
3.Zout21通过分类函数softmax转换,成概率分布S1.
4.S1通过损失函数计算得到损失值Loss.
以上就是一个完整的数据流。
详细计算过程如下:
解释一下为什么多层神经网络中有反向传播:
信号向前传播,权重的更新反向传播
1.整个过程就是前馈的意思,信号一直向前流动,最后输出,中间任意层没有信号反回上一级网络。
2.接下来将神经网络的输出值与训练样本中的输出值进行比较,计算出误差,并使用这个误差值来反向调节权重值。
输出之后,前向传播的输出值与真实值还存在一定差距,不过没关系,反向传播误差会帮助我们更新权值,缩小这些误差。
神经网络通过一种链式求导的方法,一步步将误差从后向前传播。例如:对于隐藏层和输出层之间的权重w1来说,如果我们想知道w1对整体误差产生了多少影响,可以用总误差对w1求偏导,该偏导可以使用链式法则表示。
神经网络求导的本质是为了修改权重矩阵,所以我们可以得到如下链式求导公式,看起来很长,但是一个都不能少:

在笔记中给出两个公式,结合前面笔记的神经网络结构图,可以看出在网络的最后有两个输出,分别为S1和S2,两个输出结果分别各得出一个损失函数,Loss1和Loss2.对于一个权重值来说,每个损失值都会对其产生影响,所以我们更新权重W1的时候,要分别考虑两个损失函数对其产生的影响,所以这就是笔记中出现两个求导公式原因。
接下来我们详细分析一下链式求导中的每个过程,如下:
最终得出的结果,就是将这些求导过程相乘,此时得出的Δw是一个有符号的数字,Δ的正负符号告诉了我们沿着梯度更新的方向,此时将Δ乘以一个学习率η,得到的η·Δw,就是要更新的权重数值:
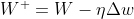
即:
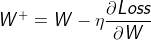
对于笔记中的,具有多个损失函数的网络来说,权重的更新形式为:
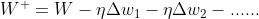



 浙公网安备 33010602011771号
浙公网安备 33010602011771号