题解：P11768 破自行车

一些闲话：

一开始写的代码是这样，然后只得了 15 pts……

while(T--){
if(l==0){
    cout<<a+b<<endl;
    continue;
}
if(k*l>=a+b){
    int ans=a%l+b%l;
    cout<<ans<<endl;
}else{
    int x=a/l;
    int ans=0;
    if(k>=x){
    int s=a%l;
    ans+=s;
    }else{
        ans+=a-k*l+b;
        cout<<ans<<endl;
        continue;
    }
    cout<<ans+b-(k-x)*l<<endl;
    }
}

赛时的时候是有正解思路的，但开始打后 5 分钟就要出门了，然后就摆烂了……
突然感觉自己 OI 学废了，连橙题都切不了了（悲）。
然后 @yuruilin2026 和@Hootime 两个神犇看见了就秒了，并且说了一句“菜就多练”。

正文：

根据幼儿园就知道的知识，如果在网格图中想从 \((0,0)\) 点到 \((a,b)\) 点，只能向上下左右移动的话最少需要 \(a+b\) 步；
然后因为自行车移动不需要时间，所以我们需要尽可能多使用自行车，然后你就会想到答案为上面那个代码。
但是这有一个问题，就是天依使用自行车在一段直线中行驶的路程可能大于那一段直线，然后再倒回来就像下面这样：
假设自行车每次可行驶 4 格，那么就会有以下两种情况。
注：红线为自行车所行驶的，黄线为走过的。

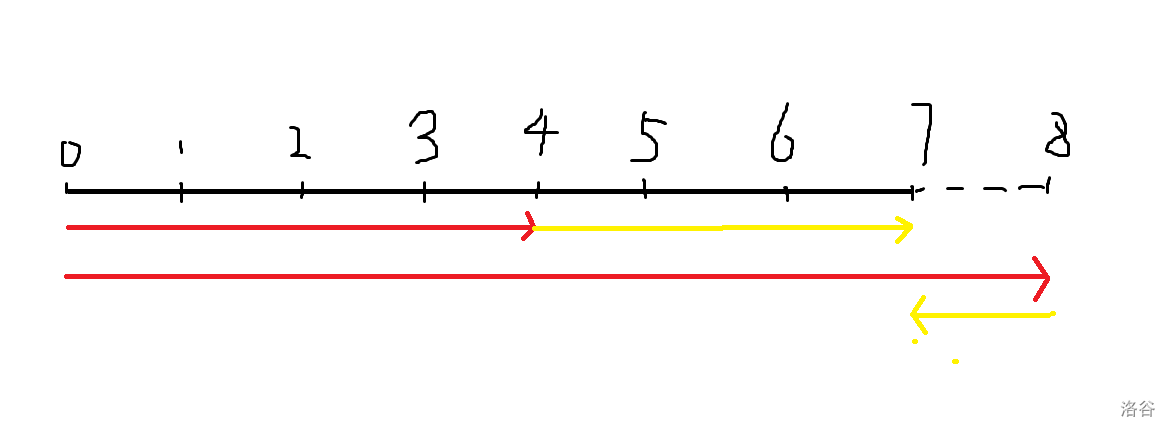
可以看出，如果只使用 1 次自行车那么需要走 3 格，但如果超出这段线段走到 8，那么只需要走 1 格。
那么，我们现在就只需要把从 \((0,0)\) 走到 \((a,b)\) 的路线分为两段，从 \((0,0)\) 到 \((0,b)\) 然后从 \((0,b)\) 到 \((a,b)\)，接着就可以套用上面分析出来的答案了，只不过要分为两段。

什么？你管我要橙题的代码？