GAMES101-03- Transformation变换

Transformation变换

Why study transformation

Modeling模型变换

Viewing视图变换

包括从3D转换为2D。

2D transformation : rotation,scale,shear

Representing transformation using matrix

Scale Matrix

横轴纵轴都缩放0.5倍，用式子表示为

用矩阵表示则如下（\(s=0.5\)）

假设是不均匀的缩放，如下

那么矩阵形式可表示如下（\(s_x=0.5,s_y=1.0\)）：

Reflection Matrix

Shear Matrix切变

怎么找出它们的矩阵形式？

答：观察水平x和垂直y上对应的变化，再考虑用矩阵来表示。

Rotate(关于原点，默认逆时针)

手推公式过程：

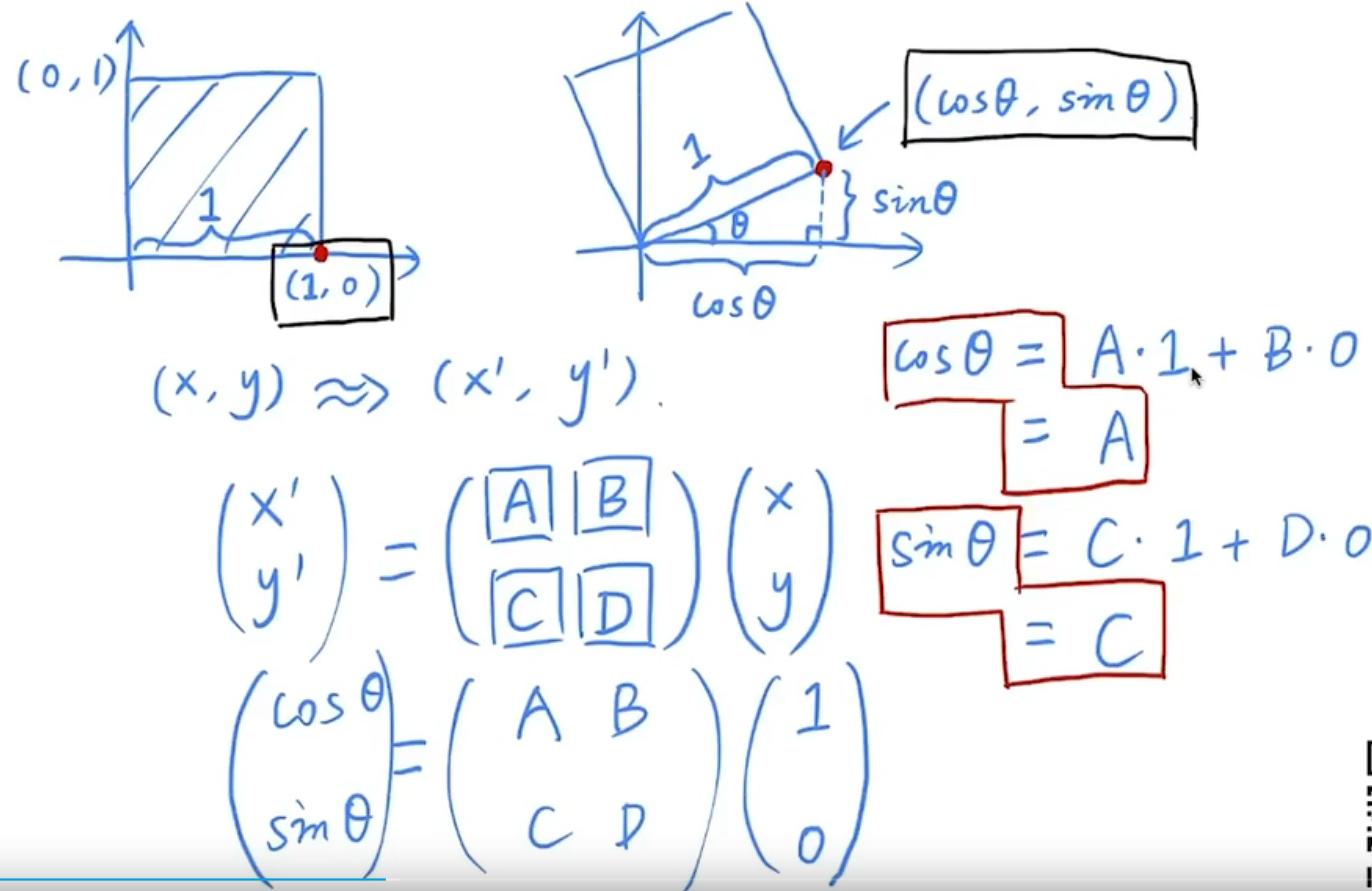
同理，可以用特殊点（0,1）推出B点和D点。

总结：

可以发现线性变换都可以写成矩阵形式如下，即矩阵乘以某输入向量等于对应输出向量。

Transiation平移

根据上图，可以发现此时式子不能再单纯地用矩阵乘以输入向量的形式了，而应该用以下形式表示：

把上图这种类似的变换，可以称为仿射变换

平移操作属于线性变换吗？

答：平移操作不属于线性变换。

Homogeneous coordinates齐次坐标

但我们不希望把平移当作一种特殊情况处理。所以思考有没有统一的方式来表示所有的变换形式呢？

答：引入齐次坐标的概念。

2维向量的第三行为什么设为0？

答：因为向量具有方向不变性，平移不变性。将向量的第三行设为0，一方面是为了保护二维向量的平移不变性，另一 方面还能保证以下操作的正确性。

需要注意的是，在齐次方程中，有个重要的概念如下：

从上面这个概念讨论，point+point等于什么呢？

答：point+point本身是没有意义的。但是从上面这个概念讨论的话，point+point等于这两个点的中点。（因为此时w为2，想要w为1点就要除以2）

将向量设为上述形式，那么此时平移变换可以表示成如下形式：

此时齐次变换就能够统一实现所有的变换形式，而所有的仿射变换都可以写成这样齐次坐标的形式。

举例说明如下：

那么引入齐次方程的代价是什么呢？

答：代价就是引入了一个额外的数字，任何一个点(x,y)都写成了(x,y,1)，任何一个向量(x,y)都写成了(x,y,0)。而对矩阵来说，原本是2x2，现在是3x3的形式（只是最后一行，一般是0，0，1（表示仿射变换的时候），代价算是比较小的）。

其他变换

Inverse Transform逆变换

Composing transforms

考虑以下变换形式：

可能变换的过程如下：先旋转再平移。

而先平移再旋转，得不出目标形式：

由上面的变换过程可以得出什么？

答：一是可以得出复杂的变换过程可以由多个简单的变换实现；二是可以得出变换的顺序是很重要的（这点也可以用矩阵不可以用交换律的思维来考虑）。

用矩阵表示上述组合变换如下：

将上述这个组合变换进行推广，可以得到如下形式（利用了矩阵的结合律）：

矩阵乘积的性质使得用一个\(A\)来表示多个矩阵\(A_i\)相乘，把复杂化为简单。

举例如下，下图中向量（x，y，1）先线性变换（旋转），再平移处理。等号右侧的式子中前两个矩阵是可以写在一起的。

Decomposing Complex Transform分解复杂变换

举例，考虑旋转不绕着原点，而是绕着点c。

那么此时就可以考虑分解。

3D transformations

三维的变换都可以用二维的变换来类比，那么三维也引入齐次坐标，那么其表示形式可以写为：

同理，对点的定义操作如下：

当然，写\((x/w,y/w,z/w,1)\)也是对的，这样就是用四个数来表示三维空间的点。

那么三维空间也可以用4x4的矩阵来表示（仿射变换的情况下，矩阵的最后一行就是0，0，0，1）：

思考，在上式写成4x4矩阵形式的时候，是先考虑线性变换呢，还是先考虑平移呢？

答：同二维空间一样，如下式子可以看出是先线性变换再平移的。所以在三维空间也是一样的，先线性变换再平移。