BZOJ3994: [SDOI2015]约数个数和

BZOJ3994: [SDOI2015]约数个数和

Description

 设d(x)为x的约数个数，给定N、M，求

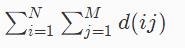
Input

输入文件包含多组测试数据。

第一行，一个整数T，表示测试数据的组数。

接下来的T行，每行两个整数N、M。

Output

 T行，每行一个整数，表示你所求的答案。

Sample Input

2
7 4
5 6

Sample Output

110
121

HINT

1<=N, M<=50000

1<=T<=50000

 

题解Here!

看到两个求和符号，立马想到 莫比乌斯反演。

但是那个 d(ij) 怎么办？

没事，我们有：

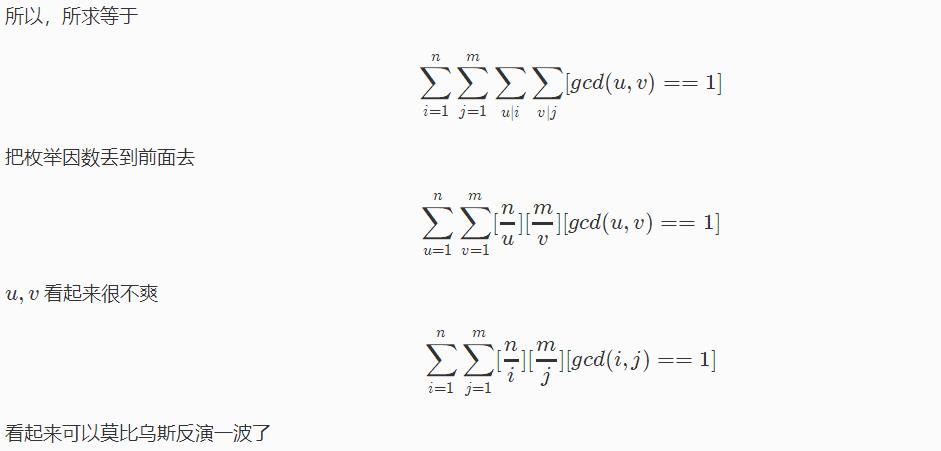
你会知道这个玩意的值就是每个数约数个数的前缀和

因为一个数的约数个数是积性函数，可以线性筛

所以这个可以 O(n) 预处理

接下来的东西就比较好算了

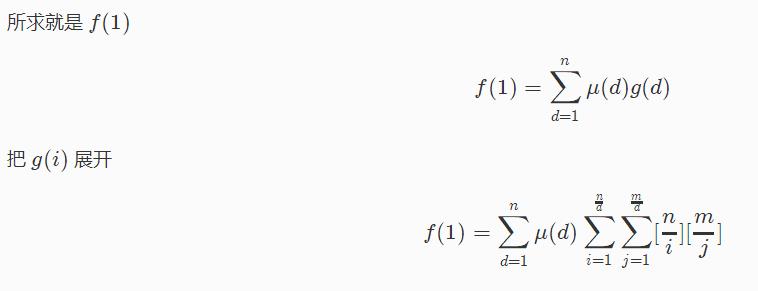
很明显，数论分块。

所以再预处理一下 μ(i) 的前缀和就行了。

附代码：

#include<iostream>
#include<algorithm>
#include<cstdio>
#define MAXN 50010
using namespace std;
int k=0,prime[MAXN],mu[MAXN],sum[MAXN];
long long f[MAXN];
bool np[MAXN];
inline int read(){
	int date=0,w=1;char c=0;
	while(c<'0'||c>'9'){if(c=='-')w=-1;c=getchar();}
	while(c>='0'&&c<='9'){date=date*10+c-'0';c=getchar();}
	return date*w;
}
void make(){
	int m=MAXN-10;
	mu[1]=1;
	for(int i=2;i<=m;i++){
		if(!np[i]){
			prime[++k]=i;
			mu[i]=-1;
		}
		for(int j=1;j<=k&&prime[j]*i<=m;j++){
			np[prime[j]*i]=true;
			if(i%prime[j]==0)break;
			else mu[prime[j]*i]=-mu[i];
		}
	}
	for(int i=1;i<=m;i++)sum[i]=sum[i-1]+mu[i];
	for(int i=1;i<=m;i++){
	    long long s=0;
	    for(int j=1,last=1;j<=i;j=last+1){
	        last=i/(i/j);
	        s+=(long long)(last-j+1)*(i/j);
	    }
	    f[i]=s;
	}
}
void work(){
    int n,m;
	long long ans=0;
	n=read();m=read();
	if(n>m)swap(n,m);
	for(int i=1,last=1;i<=n;i=last+1){
		last=min(n/(n/i),m/(m/i));
		ans+=(long long)(sum[last]-sum[i-1])*f[n/i]*f[m/i];
	}
	printf("%lld\n",ans);
}
int main(){
	int t=read();
	make();
	while(t--)work();
	return 0;
}