重抽样方法（验证集方法、留一交叉验证法LOOCV、K折交叉验证法）

验证集方法

library(ISLR)

set.seed(1)

Train<-sample(392,196) #用sample ()函数把观测集分为两半，从原始的 392 个观测中随机地选取一个有 196个观测的子集，作为训练集。

lm.fit<-lm(mpg~horsepower,data=Auto,subset=train)

attach(Auto)

mean((mpg-predict(lm.fit,Auto))[-train]^2) #用predict ()函数来估计全部392 个观测的响应变景，再用 mean() 函数来计算验证集中196 个观测的均方误差。

 

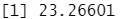
结果分析：用线性回归拟合模型所产生的测试均方误差估讨为23.27。

lm.fit2<-lm(mpg~poly(horsepower,2),data=Auto,subset=train) #用 poly ()函数来估计用二次多项式回归所产生的测试误差。

mean((mpg-predict(lm.fit2,Auto))[-train]^2)

 

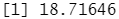
lm.fit3<-lm(mpg~poly(horsepower,3),data=Auto,subset=train) #用 poly ()函数来估计用三次多项式回归所产生的测试误差。

mean((mpg-predict(lm.fit3,Auto))[-train]^2)

 

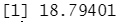
结果分析：这些结论表明，一个用 horsepoer的二次函数来拟含的模型预测mpg的效果比仅用 horsepower 的线性函数拟合模型的效果要好，而几乎没有证据表明用 horsepoer的三次函数拟合模型的效果更好。

留一交叉验证法LOOCV

#如果用 glm() 函数拟合模型时没有设定 family 参数，那么它就跟lm ()函数一样执行的是线性回归。

glm.fit<-glm(mpg~horsepower,data=Auto)

coef(glm.fit)

 

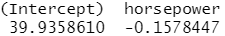
lm.fit<-lm(mpg~horsepower,data=Auto)

coef(lm.fit)

 

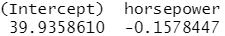
#用 glm ()函数而不是lm ()酶数来做线性回归，因为glm()可以跟 cv. glm ()函数一起使用。

library(boot)

glm.fit=glm(mpg~horsepower,data=Auto)

cv.err=cv.glm(Auto,glm.fit)

cv.err$delta

 

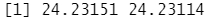
结果分析：delta 向量中的两个数字为交叉脸证的结果。

cv.error=rep(0,5)

#使用for循环拟合多项式回归模型，并计算相应的交叉验证误差

for (i in 1:5){

  glm.fit=glm(mpg~poly(horsepower,i),data=Auto)

  cv.error[i]=cv.glm(Auto,glm.fit)$delta[1]

}

cv.error

 

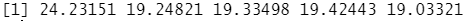
结果分析：这些结论表明，一个用 horsepoer的五次函数来拟含的模型预测mpg的效果比仅用 horsepower 的线性函数拟合模型的效果要好，而几乎没有证据表明用 horsepoer的三次函数拟合模型，四次函数拟合模型比二次拟合模型的效果更好。

K折交叉验证法

#cv. glm ()函数同样可以用于实现k折CV，令 k=10，这时一个通常的选择，然后在Auto 数据集上使用K折交叉验证，创建一个向量，把用一次到十次多项式拟告模型所产生的CV误差储存在这个向量中。

set.seed(17)

cv.error.10=rep(0,10)

for (i in 1:10){

  glm.fit=glm(mpg~poly(horsepower,i),data=Auto)

  cv.error.10[i]=cv.glm(Auto,glm.fit,K=10)$delta[1]

}

cv.error.10

 

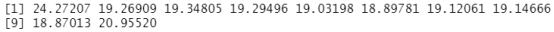
 结果分析：这些结论表明，一个用 horsepoer的九次函数来拟含的模型预测mpg的效果比仅用 horsepower 的线性函数拟合模型的效果要好，而几乎没有证据表明用 horsepoer的十次函数拟合模型比九次拟合模型的效果更好。