kNN算法及案例分析

kNN算法应用于iris数据集

 

  K最近邻，顾名思义，就是K个最邻近的样本的意思。如果一个样本的最接近的K个邻居里，绝大多数属于某个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。KNN算法有两个关键点要注意。第一个关键点是K的确定，选择一个最佳的K值取决于数据分布情况。总的来说，较小的K值能使模型更不容易受样本不均衡的影响，而较大的K值能够减小噪声的影响。第二个关键点是最近邻的定义，也就是距离定义，常用的有欧式距离、余弦距离等，具体采用哪种距离定义要根据实际的数据和业务确定。由于KNN 在确定分类决策上只依据最邻近的几个样本的类别来决定待分样本所属的类别,它只与极少量的相邻样本有关,因此它是非线性的，对于类域的交叉或重叠较多的待分样本集来说，KNN方法非常适用。

 

#选择iris数据集为例，iris共有150条1数据

head(iris)

 

#对iris进行归一化处理，scale归一化的公式为(x-mean(x))/sqrt(var(x))

iris_s=data.frame(scale(iris[,1:4]))

iris_s<-cbind(iris_s,iris[,5])

#对iris数据集随机选择其中的前100条数据作为已知分类的样本集（训练集）

sample.list<-sample(1:150,size=100)

iris.known<-iris_s[sample.list,]

#剩余50条数据作为位置分类的样本集（测试集）

iris.unknown<-iris_s[-sample.list,]

#对测试集中的每个样本计算其与已知样本的距离，因为已经归一化，此处直接使用欧氏距离

length.known<-nrow(iris.known)

length.unknown<-nrow(iris.unknown)

for(i in 1:length.unknown){

  #dis记录每个已知类别样本的距离及样本的类别

  dis_to_known<-data.frame(dis=rep(0,length.known))

  for(j in 1:length.known){

    #计算距离

    dis_to_known[j,1]<-dist(rbind(iris.unknown[i,1:4],iris.known[j,1:4]),method = "euclidean")

    #保存已知样本的类别

    dis_to_known[j,2]<-iris.known[j,5]

    names(dis_to_known)[2]="Species"

  }

  #按距离从小到大排序

  dis_to_known<-dis_to_known[order(dis_to_known$dis),]

  #kNN算法中的k定义了最邻近的k个已知数据的样本

  k<-5

  #按因子进行计数

  type_freq<-as.data.frame(table(dis_to_known[1:k,]$Species))

  #按计数值进行排序

  type_freq<-type_freq[order(-type_freq$Freq),]

  #记录频数最大的类型

    iris.unknown[i,6]<-type_freq[1,1]

}

names(iris.unknown)[6]="Species.pre"

#输出分类结果

iris.unknown[,5:6]

 

案例1：股票市场数据的应用

library(ISLR)

names(Smarket)

dim(Smarket)

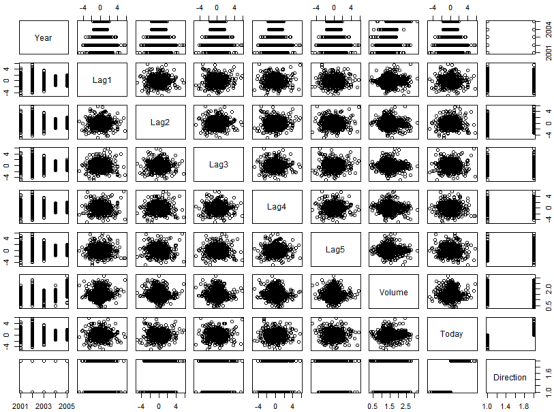
summary(Smarket)

pairs(Smarket) #pairs（）函数用于返回一个绘图矩阵，由每个 DataFrame 对应的散点图组成。

cor(Smarket[,-9]) #cor ()函数可以计算所有预测变最两两之间相关系数的矩阵。

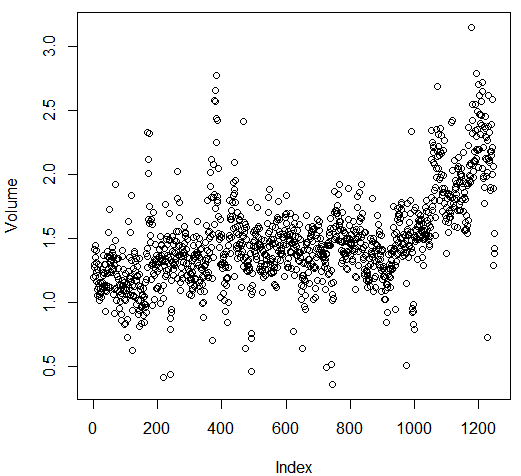
解释：相关的是 Year和Volume ，通过画图可以观察到 Volume 随时间一直增长，也就是说从 2001 年至 2005 年平均每日股票成交盘在增长。

attach(Smarket)

plot(Volume)

library(class)

train.X=cbind(Lag1,Lag2)[train,] #包含与训练数据相关的预测变量矩阵

test.X=cbind(Lag1,Lag2)[!train,] #包含与预测数据相关的预测变量矩阵

train.Direction=Direction[train] #包含训练观测类标签的向量

set.seed(1)

knn.pred=knn(train.X,test.X,train.Direction,k=1) 

table(knn.pred,Direction.2005)

 

(83+43)/252

 

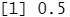
#K=1时的结果不理想，只有 50% 的观测得到正确的预测，这可能因为 K= 1的模型过于光滑，使用 K=3 重复上述实验。

knn.pred=knn(train.X,test.X,train.Direction,k=3) 

table(knn.pred,Direction.2005)

 

mean(knn.pred==Direction.2005) #结果略有改观

 

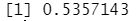
案例2：大篷车保险数据的一个应用

对 ISLR库中的 Caravan (大篷车)数据集运用 KNN 方法。该数据集包括 85 个预测变量，测量了 5822 人的人口特征。响应变最为 Purchase (购买状态) .表示一个人是否会购买大篷车保险险种。在该数据集中，只有 6% 的人购买了大篷车保险。

dim(Caravan)

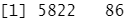
attach(Caravan)

summary(Purchase)

 

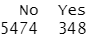
348/5822

 

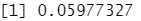
standardized.X=scale(Caravan[,-86]) #标准化数据，第86列为Purchase状态，不适合标准化

var(Caravan[,1])

 

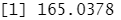
var(Caravan[,2])

 

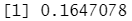
var(standardized.X[,1]) #命令standardized.X 将每列均值为0，标准差置为 1 。

 

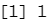
var(standardized.X[,2])

 

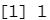
test=1:1000

train.X=standardized.X[-test,] #训练集

test.X=standardized.X[test,] #测试集，样本量为1000

train.Y=Purchase[-test] #训练集标签

test.Y=Purchase[test] #测试集标签

set.seed(1)

knn.pred=knn(train.X,test.X,train.Y,k=1)

mean(test.Y!=knn.pred) #KNN 错误率在 1000 个部试观测下略低于 12% 

 

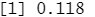
mean(test.Y!="No")

 

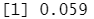
table(knn.pred,test.Y)

 

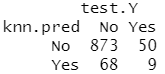
9/(68+9)

 

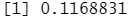
结果分析：事实表明 K=1在被预测有购买倾向性的客户上 KNN 模型比随机预测效果好得多，77 名这样的客户，其中9名，也就是 1 1. 7% 事实上购买了保险。这个结果的概率是随机猜测得到结果概率的两倍。

knn.pred=knn(train.X,test.X,train.Y,k=3)

table(knn.pred,test.Y)

 

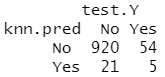
5/26

 

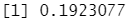
knn.pred=knn(train.X,test.X,train.Y,k=5)

table(knn.pred,test.Y)

 

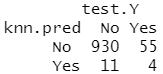
4/15

 

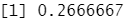
结果分析：K=3 时，成功率增加至 19% ，而当 K=5 时，成功率变为 26.7% ，这比随机猜想所得成功率的四倍还多。这似乎表明 KNN 在一个复杂数据集中可以发现一些真实的模式。

#案例3：鸢尾花数据集

 

library("class")

train.idx<-sample ( 1:nrow (iris) , 100)

iris.train <-iris[train.idx, ]

iris.test<- iris[-train.idx,]

resknn <- knn (train = subset (iris.train,select =-Species), test = subset(iris.test,select=-Species) , cl=iris.train$Species, k=2)

table(iris.test$Species, resknn,dnn=c("Actual","predicted"))