浅层神经网络

1 神经网络

1.1 浅层神经网络

    

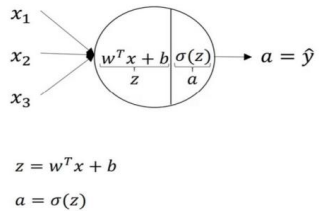
如上所示，首先你需要输入特征x，参数w和b，通过这些你就可以计算出z,接下来使用z就可以计算出a,我们将的符号换为表示输出y^ ⟹ a = σ(z),然后可以计算出 loss function L(a, y)

 1.2 神经网络的表示（Neural Network Representation）

 

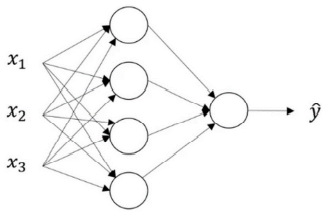
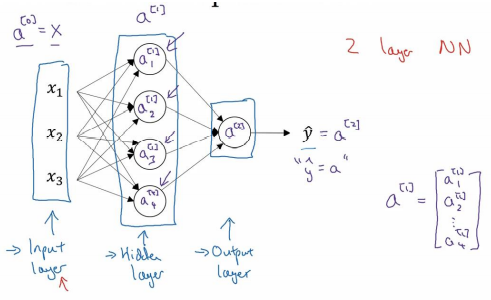
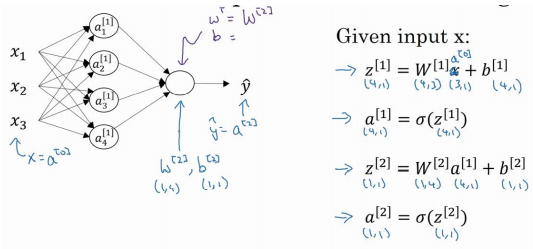
我们有输入特征x1、x2、x3，它们被竖直地堆叠起来，这叫做神经网络的输入层，它包含了神经网络的输入；然后这里有另外一层我们称之为隐藏层即图中间的4个结点，在一个神经网络中，当你使用监督学习训练它的时候，训练集包含了输入x也包含了目标输出y，所以术语隐藏层的含义是在训练集中，这些中间结点的准确值我们是不知道到的，也就是说你看不见它们在训练集中应具有的值,你能看见输入的值，你也能看见输出的值，但是隐藏层中的东西，在训练集中你是无法看到的；最后一层只由一个结点构成，而这个只有一个结点的层被称为输出层，它负责产生预测值。

符号：使用a^[0]可以用来表示输入特征,a表示激活的意思，它意味着网络中不同层的值会传递到它们后面的层中，输入层将x传递给隐藏层，所以我们将输入层的激活值称为a^[0]；下一层即隐藏层也同样会产生一些激活值，那么我将其记作a^[1]，所以具体地，这里的第一个单元或结点我们将其表示为a^[1]₁，第二个结点的值我们记a^[1]₂以此类推,输出层将产生某个数值a，它只是一个单独的实数，所以的y^值将取为a^[2].

 

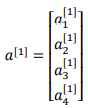
最后，我们要看到的隐藏层以及最后的输出层是带有参数的，这里的隐藏层将拥有两个参数w和b，我将给它们加上上标 (w^[1],b^[1])，表示这些参数是和第一层这个隐藏层有关系的,w是一个 4x3 的矩阵，而b是一个 4x1 的向量，第一个数字 4 源自于我们有四个结点或隐藏层单元，然后数字 3 源自于这里有三个输入特征，相似的输出层也有一些与之关联的参数w^[2]以及b^[2]。从维数上来看，它们的规模分别是 1x4 以及 1x1，1x4 是因为隐藏层有四个隐藏层单元而输出层只有一个单元。

1.3 计算一个神经网络的输出（Computing a Neural Network's output）

只有一个隐藏层的简单两层神经网络结构（输入不算层数）,其中，x表示输入特征，a表示每个神经元的输出，w表示特征的权重，上标表示神经网络的层数（隐藏层为 1），下标表示该层的第几个神经元.

 

 神经网络的计算:

逻辑回归的计算有两个步骤，首先你按步骤计算出z，然后在第二步中你以 sigmoid 函数为激活函数计算z（得出a），一个神经网络只是这样子做了好多次重复计算.

 

对于上面两层的神经网络，我们从隐藏层的第一个神经元开始计算，小圆圈代表了计算的两个步骤：

   

隐藏层的第二个以及后面两个神经元的计算过程一样，只是注意符号表示不同，最终分别得到a^[1]₂、a^[1]₃、a^[1]₄，详细结果见下:

   向量化计算:  z^[n]=w^[n]x+b^[n]

                      a^[n]=σ(z^[n])

  

 

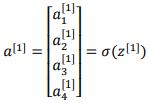
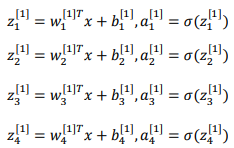
   多样本向量化：z^[n](i)=w^[n](i)x+b^[n](i)      #i从1到m

                      a^[n](i)=σ(z^[n](i))

     

 

 

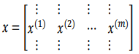
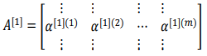
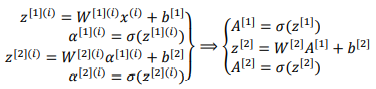
从小写的向量x到这个大写的矩阵X，只是通过组合x向量在矩阵的各列中,z^[1](1)，z^[1](2)等等都是z^[1](m)的列向量，将所有m都组合在各列中，就的到矩阵z^[1],a^[1](1)，a^[1](2)，……，a^[1](m)将其组合在矩阵各列中，如同从向量x到矩阵X，以及从向量z到矩阵Z一样，就能得到矩阵A^[1],对于Z^[2]和A^[2]，也是这样得到.