关于浮点数

浮点数的取值范围

定点数存储

什么是定点数？

定点数（fixed-point number）是在计算机中表示数字的一种方式，它的特点是数的小数点位置是固定的。具体来说，定点数通常用来表示整数和纯小数，分别称为定点整数和定点小数。小数点的位置由计算机设计者在机器的结构中指定，并且这个位置在运算过程中保持不变。

定点数定义

定点整数：在这种表示法中，小数点被固定在数值部分的最后边，即数的最低位之后。这意味着整个数值部分被视为整数部分，没有小数部分。
定点小数：在小数表示法中，小数点被固定在符号位和第一位数值位之间，或者对于无符号数，小数点被约定在最前边。这意味着数值部分包含了小数部分，且小数点的位置是固定的。

定点数特点

表示范围有限：由于小数点的位置是固定的，因此用定点数表示的数值范围是有限的。特别是当需要表示非常大或非常小的数时，定点数可能无法满足需求。
精度固定：由于小数位数固定，定点数所能表示的小数精度也是固定的。这意味着在表示某些需要高精度的小数时，可能会出现舍入误差。
运算简单：与浮点数相比，定点数的运算规则相对简单。因为小数点的位置不变，所以在进行加减乘除等运算时，不需要考虑小数点的移动问题。
硬件实现容易：在硬件数字电路中，许多处理器都是整数处理器。因此，使用定点数进行运算可以更容易地利用这些处理器的整数运算能力，从而提高运算效率。

定点数应用场景

定点数在实际应用中有着广泛的应用场景。例如，在嵌入式系统、数字信号处理等领域中，由于资源受限和实时性要求高等特点，定点数运算往往比浮点数运算更受欢迎。此外，在一些需要高精度计算但又不需要处理极大或极小数值的场合（如金融计算、图像处理等），定点数也是一个很好的选择。

定点数存储举例说明

浮点数存储

浮点数公式

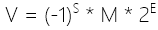
组成部分依次是“符号 * 尾数 * 阶码”：

符号（sign）决定这个数是正数（s = 0）还是负数（s = 1）；
尾数（significand）决定这个数的精度，这里是用定点法表示；
阶码（exponent）决定这个数的范围，它是一个加权值，权重自然是 2 的 E 次幂。

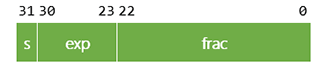
C语言中float和double的封装格式：

float
double

从上面结构我们可以看出以下信息：

C语言中，对于浮点数的封装顺序是：符号位（S）+阶码位(需要计算后才能得到阶码位)+尾数位（根据不同情况有不同计算获得）
float封装格式中，三个位置分配空间分别：分配 1 位，8 位和 23 位
double封装格式中，三个位置分配空间分别：分配 1 位，11 位和 52 位

根据阶码值的不同，所出现4种情况

规格化的值

这是最普遍的情况，当 exp 字段不全为 0，也不全为 1 的时候，属于这种情况。
在这种情况下，阶码字段被解释为以偏置（biased）形式表示的有符号整数。
阶码位计算：E = e - Bias
其中，e 是一个无符号数，其值为 exp 字段表示的值；Bias 是一个等于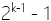
（k 即阶码字段的位数）的偏置值。
因为float界面字段位数是8，而double是11，由此不难推导出指数 E 的取值范围是 -126 ~ 127（float）和 -1022 ~ 1023（double）。
对于 frac 字段则被解释为描述小数的值，如果我们把该值称之为 f，则 0 <= f < 1，而尾数被定义为 M = 1 + f
因此，在这种情况下，尾数的第一位总是 1。
非规格化的值

当 exp 字段全为 0 的时候，所表示的数就是非规格化形式。
在这种情况下，此处阶码的值是E = 1 - Bias，此处E = e - Bias并不适用，这里是为了确保非规格化数有一个比所有规格化数都小的指数，从而能够表示接近零的数值。因此，即使存储的指数部分是0，非规格化数的实际指数E也是1 - Bias。对于单精度浮点数，这意味着E = 1 - 127 = -126。这是非规格化数能够表示的最小指数值，使得它们能够表示非常接近于零的数值。
而尾数被定义为 M = f
因此，在这种情况下，尾数即小数的值（第一位不是 1）。
非规格化数用于表示那些非常接近 0.0 的数。
无穷大

当 exp 字段全为 1，且 frac 字段全为 0 的情况下，该浮点数表示无穷。
即 s = 0，结果为正无穷；s = 1，结果为负无穷。
当我们把两个非常大的数相乘，或者除以 0 的时候，无穷能够表示溢出的结果。
NaN（Not a Number，不是一个数）