二分查找算法练习

题目

1. 704二分查找
   
   标准的二分查找算法，需要注意的是，最大坐标和最小坐标每次重新赋值后，最大坐标需要-1，最小坐标需要+1，这样用来平衡数组的个数的奇偶

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        max_num = len(nums) - 1
        min_num = 0
        while max_num >= min_num:
            con_num = int((max_num + min_num) / 2)
            # con_num = (right - left) // 2 + left 这里也可以这样写，这种写法可以避免超出给定范围的情况，该写法必然在范围中
            if nums[con_num] == target:
                return con_num
            if nums[con_num] > target:
                max_num = con_num - 1
            if nums[con_num] < target:
                min_num = con_num +
        return -1

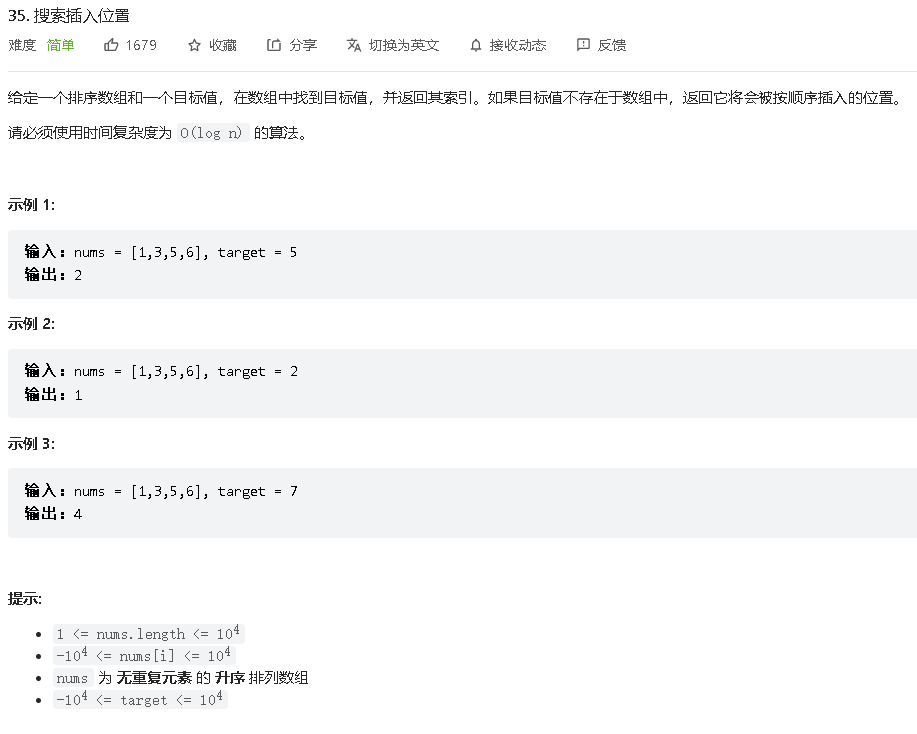
2. 35搜索插入位置
   

解题思路

这道题是在题目704上面的一个变种，只是把704中的返回-1改成返回可以插入的下标。我们在通过设定两个指针，分别代表数组最大值和最小值的下标。因为需要兼容数组中个数的奇偶，所以每次改变最大值或者最小值的时候，需要在原本的中间下标上加一或者减一。同时，因为是这种写法，所以当目标值无法从数组中找到的时候，那么原本的最大值一定是小于最小值的，所以返回值一定是原本的最小值的函数，也就是min_num

代码

class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        max_num = len(nums) - 1
        min_num = 0
        while min_num <= max_num:
            con_num = int((max_num + min_num) / 2)
            if nums[con_num] == target:
                return con_num
            if nums[con_num] > target:
                max_num = con_num - 1
            else:
                min_num = con_num + 1
        return min_num

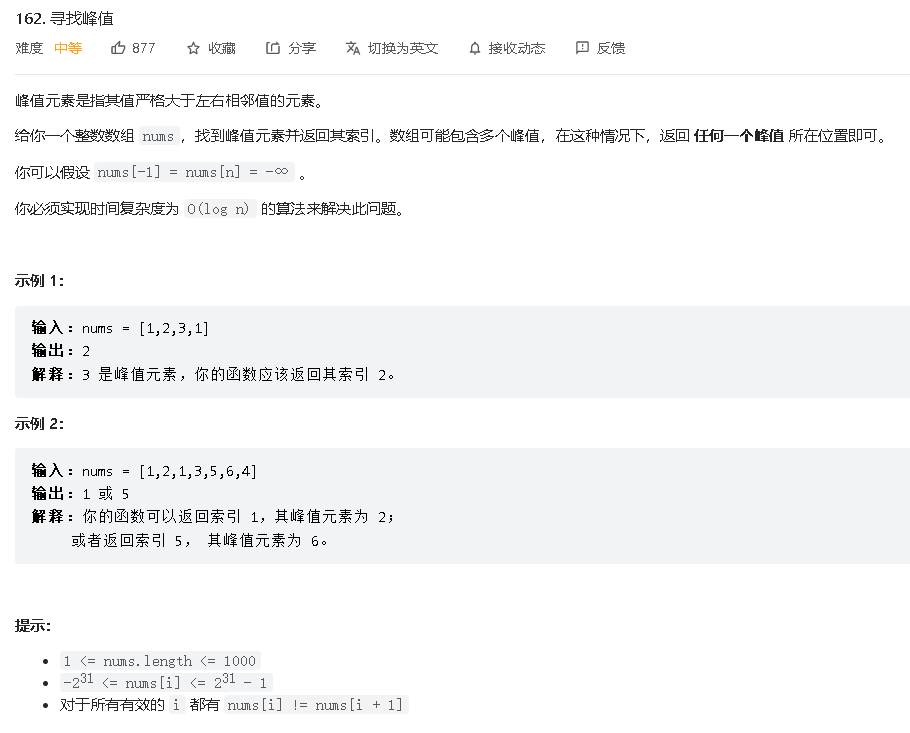
3. 162寻找峰值
   

解题思路

其实整体的思路很简单，就是比较当前值和前后两个值的变化。因为题目中已经给出，这个数组的最前和最后都是负无穷的。所以两端方向肯定可以找到最大值。而且这里并没有要求找到全部峰值，只需要找到其中一个即可，所以这里可以尝试使用二分的思路。虽然二分查询的条件是数组必须有序，但是，正是因为这个条件。我们可以取反。比如原本前面单调递增的情况突然出现拐点，那么这个拐点就是峰值。也就是说我们只需要在二分查询的方法中新增一个判断拐点的条件即可

class Solution:
    def findPeakElement(self, nums: List[int]) -> int:
        n = len(nums)
        max_num = n - 1
        min_num = 0

        def get(i: int) -> int:
            if i == -1 or i == n:
                return float('-inf')
            return nums[i]

        while min_num <= max_num:
            con_num = int((max_num + min_num) / 2)
            if get(con_num - 1) < get(con_num) > get(con_num + 1):
                return con_num
            elif get(con_num - 1) > get(con_num):
                max_num = con_num - 1
            elif get(con_num + 1) > get(con_num):
                min_num = con_num + 1

4. 74