堆算法

堆是什么

堆是一种特殊的二叉树结构，分为最小堆和最大堆
最小堆：从上到下，节点数据逐层变大的完全二叉树
最大堆：从上到下，节点数据逐层变小的完全二叉树

堆的操作

每次对堆进行增加，删除的时候，均会重新对二叉树进行排序，以保证最小堆或者最大堆，并且满足完全二叉树结构

时间复杂度

堆化：O(N)

算法题

1. 215数组中的第K个最大元素
   
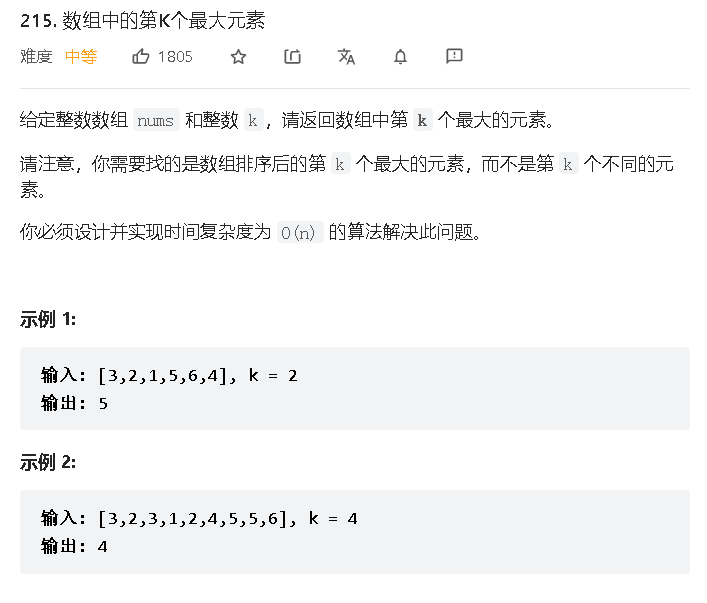
   这里我想出来两个解法，其实这里可以使用快速排序和快速选择解答

解法一：排序

class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        nums.sort()
        return nums[0-k]

解法二：使用堆

思路一：构建一个负数的最大堆，然后依次删除，最后获取堆顶并且乘以-1即可

import heapq
class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        for i, v in enumerate(nums):
            nums[i] = v * -1

        heapq.heapify(nums)
        
        while k > 1:
            heapq.heappop(nums)
            k = k - 1

        for j, v in enumerate(nums):
            nums[j] = v * -1
            
        return nums[0]

思路二：构建一个有k值限制的最小堆，每次新增数据都把最小值移除，最后保留的堆顶，就是我们需要的数据

import heapq
class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        nums_k = nums[:k]
        heapq.heapify(nums_k)
        for i in nums[k:]:
            heapq.heappush(nums_k, i)
            heapq.heappop(nums_k)
            
        return nums_k[0]

2. 692前k个高频单词
   
   这道题需要注意两点，比较的时候首先比较单词出现频率，如果评论一致，则比较单词第一个首字母，这里的字典顺序代表字母越小，值越大，因为我们最后返回的数组是降序排列
   在python中我们可以调用heapq模块，它默认是生成最小堆(也可以使用最大堆去解答)。如果需要修改比较规则，则需要弄一个额外的类，并对这个类的__lt__或者__gt__这两个魔法方法进行重写

• 代码如下

import heapq
import collections
class myheapq:
    def __init__(self, k, v):
        self.k = k
        self.v = v
    
    def __lt__(self, other):
        if self.v != other.v:
            return self.v < other.v
        else:
            return self.k > other.k

class Solution:
    def topKFrequent(self, words: List[str], k: int) -> List[str]:
        arr = []
        freq = collections.Counter(words)
        for key, v in freq.items():
            heapq.heappush(arr, myheapq(key, v))
            if len(arr) > k:
                heapq.heappop(arr)
        a = [heapq.heappop(arr).k for _ in range(len(arr))]
        return a[::-1]