几何概型
几何概型
使用方向:线段,平面,立体
公式:P(A)=μ(G)/μ(Ω)
- 列题一:
如图所示,长方形有一半是阴影部分,如果这时候扔一个质点,该质点落到阴影部分的概率是多少?

答:因为有一半是阴影部分,所以落下去的概率是1/2 - 列题二:
有一个线段被平均分为三段,向这个线段扔出一枚质子,求该质子落到中间线段的概率
因为是均等的三段,所以落到中间概率为1/3 - 列题三:甲,乙两人相约6-7点见面,先到者需要等待十五分钟,如果超过则不再等待,且在这一小时内,甲乙在任意时刻都可能到达。那么甲乙再这一小时内见面的概率是多大?
分析:甲乙两人在这六十分钟内的任意时刻都可以到达,且分为三种情况,甲先到,乙先到,甲乙同时到。
那么假设,A是两人见卖的概率,X是甲到的时间,Y是乙到的时间。
得到图示:
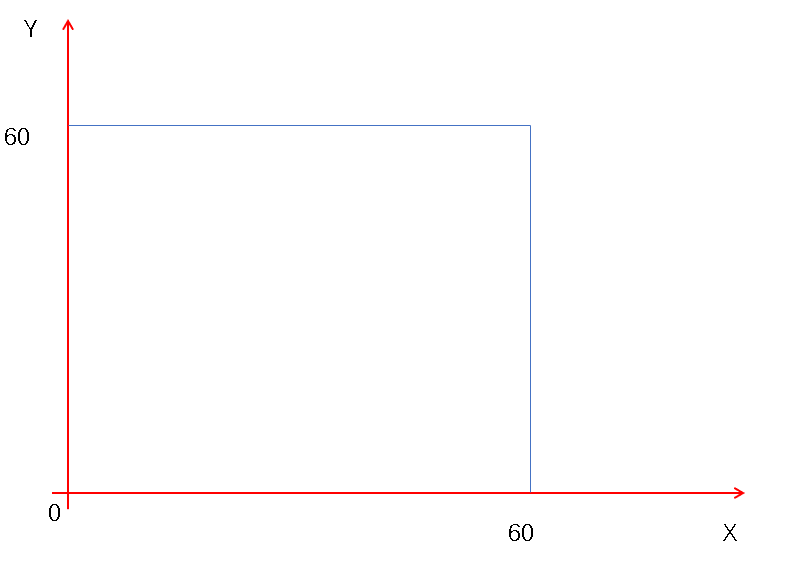
由此图我们可以得知,甲乙见面的所有事件的全集为图中的正方形
然后当两人同时到达的时候,则为x=y,也就是如图种所示
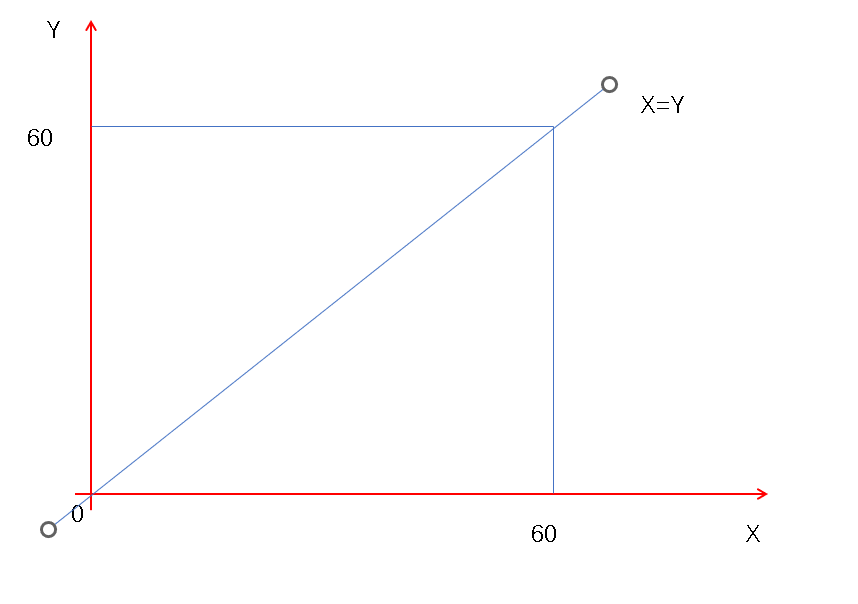
这时候分当甲先到的时候和乙先到的时候,这两个情况:- 甲先到:y-x<=15,且y-x>=0,所以y<=x+15
- 乙先到:x-y<=15,且x-y>=0,所以y>=x-15
带入原点计算,当y=0时,x=15.当x=0时候,y=15,所以可以得到下图:

得到阴影部分的面积就用正方形-两个三角形面积即可:
(6060-2(1/2)*(60-15)2)/602=0.43756
原视频图:

- 列题四:蒲丰投针问题:

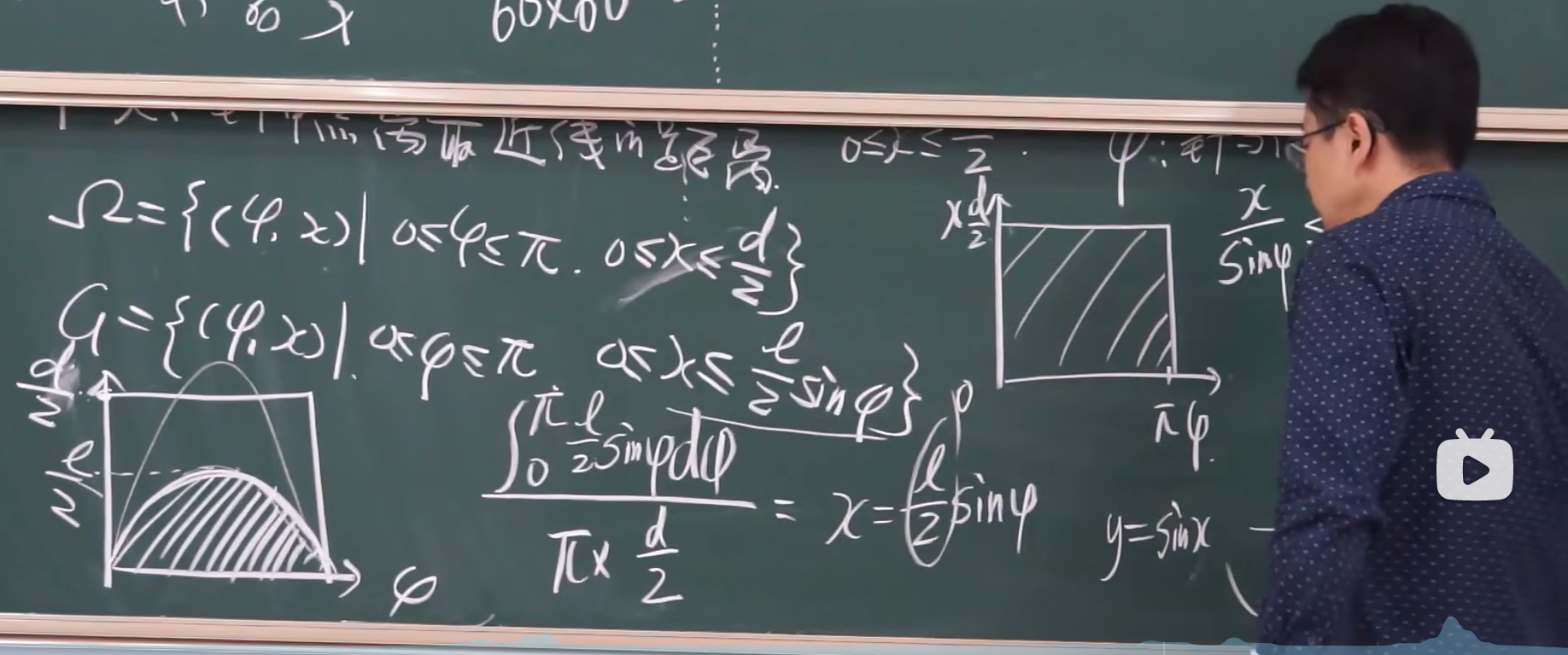

总结
几何概率模型与古典概率模型有一样的性质,但是几何概率模型具有完全可加性
完全可加性:前提是两两互不相容
公式:
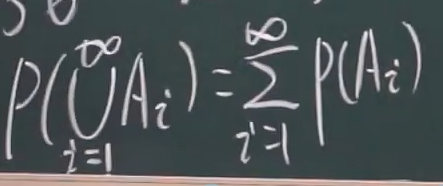



 浙公网安备 33010602011771号
浙公网安备 33010602011771号