古典概型（排列组合）

古典概率模型

1. 满足条件：
   • 有限个样本点
   • 等可能性
2. 公式：
   P(A)=(A的有利样本点)/(Ω中样点总数)=(A中包含的基本事件数)/(基本事件总数)
3. 排列组合两大原理：
   • 加法原理：几类方案选择
   • 乘法原理：分成几个步骤
     举例：
     这里有三种馒头，四种米饭可以作为主食选择：这个就是加法，为并集
     这里先吃三种馒头，再吃四种米饭：这个就是乘法原理，为交集

排列类型：

1. 不重复排列：从n个不同元素中取出m个不同元素进行排列，不放回。
   公式为：n(n-1)(n-2)....(n-m+1)=n!/(n-m)!
   

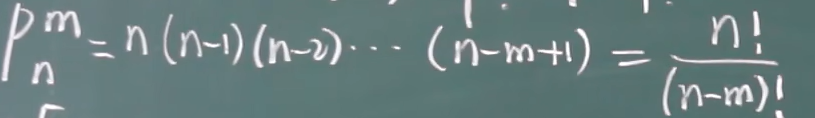
2. 全排列，从n个元素取出n个元素
   公式：n(n-1)(n-2)....321=n!
   
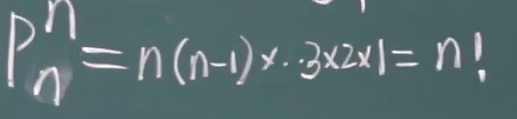
   注意：2!=2，1!=1, 0!=1
   
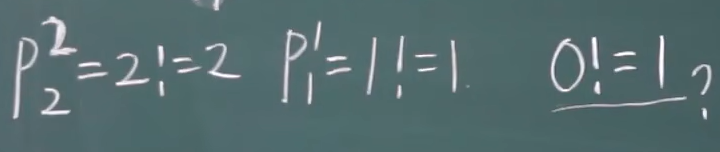
   问题：0!为啥等于1？
   解释一：因为m! = m(m-1)!,比如10!=109!,所以1!=1(1-1)!，所以1!=10!。又因为1!=1，所以0!=1
   解释二：按照场景描述，在0个元素中取出0个元素有且只有一种方案，就是什么都不做，不取值。所以0!=1
   解释三：因为从n个元素中取出m个元素进行排列，则有公式为：n(n-1)(n-2)...(n-m+1)=n!/(n-m)!,所以，当m等于n的时候，则为n!/0!。又因为全排列中n(n-1)....321=n!,所以可以得到n!/0!=n!，所以0!=1

3. 0^{0为啥是无意义的呢？曾经有个公式为a}0=1,当a≠0时。推到过程如下：
   比如5^{0=1的原因是：5}(1-1)=5^1/51=1，所以0⁰⁼⁰(1-1)=0^1/01=0/0。因为0作为了分母了，所以0^0是无意义的

4. 重复排列：从n个不同元素中取出m个进行排列，放回
   公式：nnn...*n=n^m
   组合：从n个不同元素中取出m个不同元素
   公式：
   

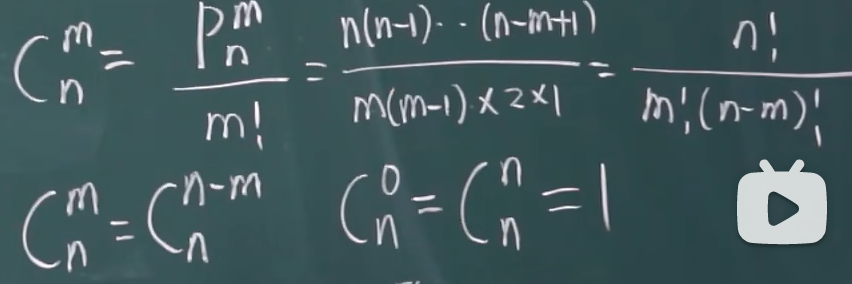
5. 例题：
   第一题：一套五卷m的选集，放书架上，求自左向右或者自右向左是1，2，3，4，5的概率
   书籍摆放顺序有两种，总的摆放顺序为5！种
   2/5!=1/60
   第二题：有四个邮筒，分别是1，2，3，4.现在又a，b两封信。求前两个邮筒各投入1封的概率
   第一封信投入的概率为1/4，第二封信概率也是1/4,所以总共16个情况，然后两封信分别在前两个邮筒的组合方式是两种
   2!/44=1/8
   第二个邮筒恰有一封信概率为：
   两封信种的任意一封都可以放在第二个邮筒中，然后剩下的那封信，则放在其他三个邮筒中，所以是两个组合乘以三个组合等于六个组合，而两封信投入邮筒的组合为16种，所以概率为6/16
   
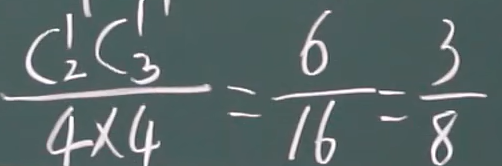
   投入不同邮筒概率：
   (43)/16=12/16
   第三题：有5个白球，4个黑球，任取3个球
   
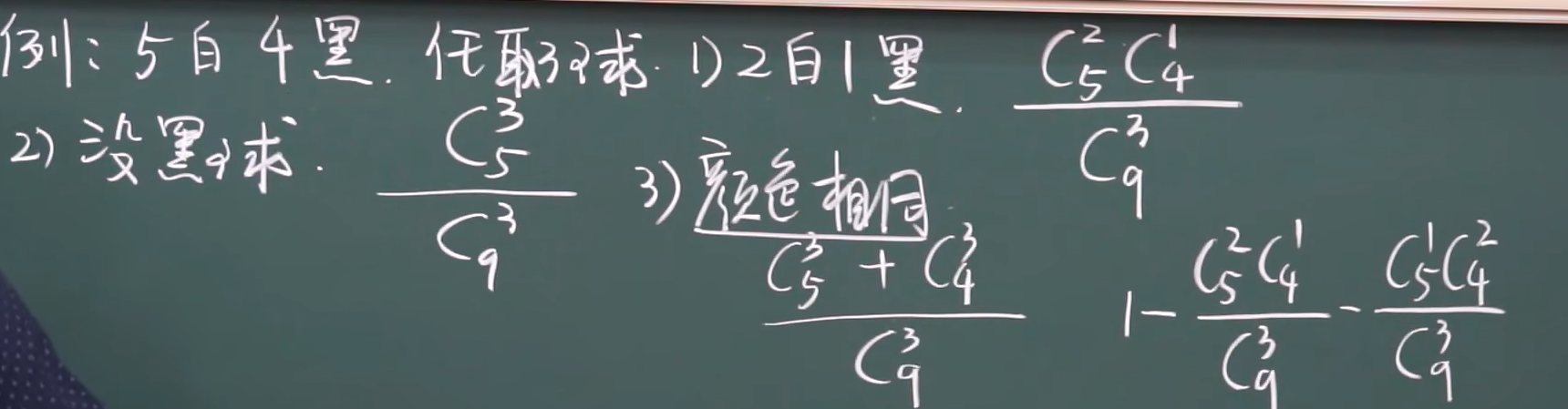
   第四题：有a个白球，b个黑球，任取一个，求是白球的概率
   a/(a+b)
   第五题：a个白球，b个黑球，从种接连取出m个(1<=m<=a+b),第m次是白球的概率
   

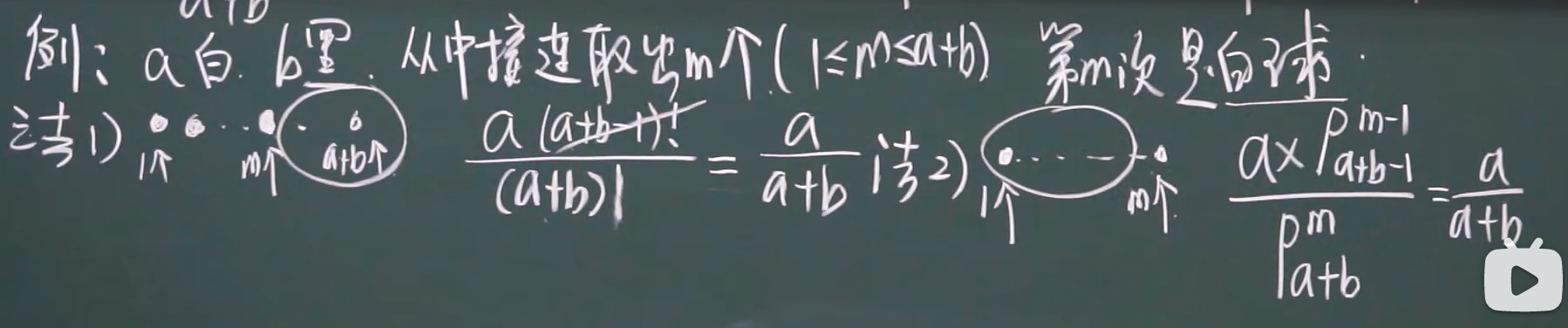
6. 古典性质：

   • 非负性：0<=P(A)<=1
   • 规范性：P(Ω)=1，P(∅)=0
   • 有限可加：A1A1...An互不相容，也就是P(A1+A2+...+An)=P(A1)+P(A2)+...+P(An)
   • 缺点：
     • 有限个结果
     • 必须是等可能性