随机实验与随机事件
引言
- 确定性(必然):一定发生,一定不发生
- 随机性现像(偶然):可能发生,可能不发生
- 统计规律:做大量实验,期望从中找出规律
1.1 随机事件
- 试验:观察,测量,实验
- 随机实验三个要求:①在相同条件下可重复;②实验结果不止一个;③无法预测最终结果
- 实验结果用‘E’表示
- 事件:每种结果都是一个事件
- 随机事件:可能会发生的事件,也可能不发生的事件。一般用字母A,B,C等表示
- 基本事件:相对于实验目的来说,事件不能再分(或者不必再分了)
- 复合事件:由基本事件复合而成
1.2 必然事件
一定发生,符号:Ω,读作:欧米噶
1.3 不可能事件
一定不发生,符号:∅,读作:fai
1.4 样本空间
所有基本事件的集合,其实就是必然事件
1.5 样本点
样本空间中的元素,其实就是其中的基本事件
举例:
- 抛出一枚硬币,看正反,样本空间为:Ω=
- 抛出一枚色子,得到的点数的样本空间为:Ω=
- 抛出两枚硬币,看正反的样本空间为:Ω=
- 电话交换机单位时间内的呼叫次数,样本空间为Ω=
- 在[a,b]中扔一个质子(一个纯粹的点),则求这个质子的坐标的样本空间:Ω=[a,b]
- 向平面内扔一个质子,求这个质子的坐标:Ω=
- 向三位空间扔一个质子,则坐标为:Ω=
1.6 事件的集合表示
- 比如表示一个色子数目不大于三的集合:A=
- 表示偶数,不大于7的事件集合:A=
小结总结
Ω = 必然事件 = 样本空间 = 全集
∅ = 不可能事件 = 空集
一般情况下,正常的事件都是Ω的子级
2.1 事件之间的关系
- 包含关系,A⊂B,读作A包含于B,如果A发生,则会导致B发生。也可以写成B⊃A,读作,B包含A
图示:

- ∅⊂A⊂Ω,这个公式永远成立
- 元素属于集合,元素与集合之间的地位是不对等的:ω∈Ω
- 集合A包含于集合B或者集合B包含集合A,两个是集合,地位是对等的:A⊂B(B⊃A)
- 两个事件相等,如果B⊃A,并且A⊂B,则A=B
- 并集(和),A与B中至少有一个发生:A∪B(A+B)
图解:

- A并B肯定是包含A(B)的:A∪B⊃A
- 如果B包含A,则A∪B=B
- 集合A加上自己本身,就是等于自己(集合中的元素不重复):A+A=A
- A∪∅=A,A∪Ω=Ω
- 交集(积),A和B同时发生:A∩B或者是A*B(简写:AB)
图解:
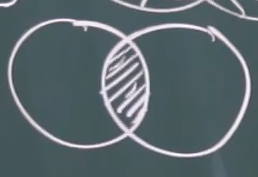
- 如果A与B不相交,则A∩B为空集。如果B包含A,则A∩B=A
- A∩B⊂A
- A∩A=A
- A∩∅=∅
- A∩Ω=A
- 无限可列个:能按照某种规律排成一个序列
- A1∪A2∪A3...∪AN...
- A1∩A2∩A3...∩AN...
- 自然数:0,1,2,3.....n....
- 差集,A发生而B不发生,去除AB的公共部分:A-B=A-AB
- 如果A于B不相交,则A-B=A
- 如果A中包含B,则从A中去除B
- 如果B中包含A,则A-B=∅
图解:
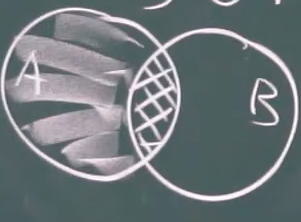
2.2 互不相容事件
A,B不同时发生,A∩B=∅
图解:

- N个事件互不相容:A1A2A3...AN,写作AiAj=∅,读作两两互不相容
- 对立事件:A,B互不相容,且A∪B=Ω,AB=∅
- 对立事件和互不相容事件的差异:
- 互不相容事件图解:
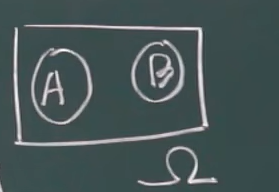
- 对立事件图解
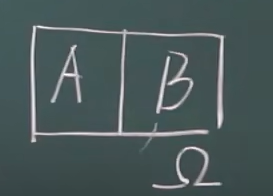
- 互不相容事件图解:
- 如果B是A的对立事件,读作:A等于B逆,记作
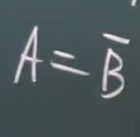
注意:A逆的逆就等于A
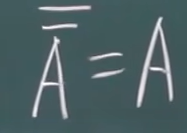
- A-B=A-AB=A∩B逆:
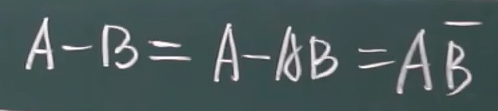
- 联系于区别:
- 两个事件对立,则一定是互不相容的
- 互不相容适用于多个事件,但是对立只适用于两个事件之间
- 如果两个事件互不相容,表示不能同时发生,但是也可以都不发生
- 对立事件是有且只有一个发生
- 完备事件组
如果A1A2....An两两互不相容,并且所有求并等于Ω - 事件之间的运算律
- 交换律:A∪B=B∪A,A∩B=B∩A
- 结合律:(A∪B)∪C = A∪(B∪C),(A∩B)∩C = A∩(B∩C)
- 分配律:(A∪B)∩C=(A∩C)∪(B∩C),(A∩B)∪C = (A∪C)∩(B∪C)
- 对偶律:

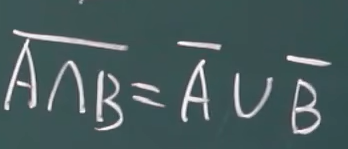
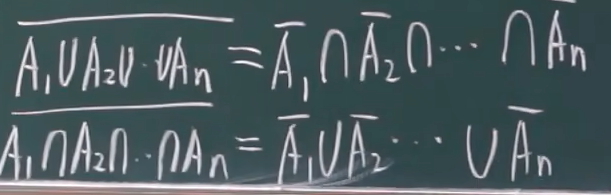
- 举例
- 例一

- 例二

- 例三

- 例一
2.4 事件的概率
- 概率的初等描述
事件的概率:发生的可能性的大小,记作为P(A) - 性质:
- P(Ω)=1,P(∅)=0
- 0<=P(A)<=1



 浙公网安备 33010602011771号
浙公网安备 33010602011771号