复杂度

时间复杂度和空间复杂度

时间复杂度

1. 什么是时间复杂度
   • 算法的执行效率
   • 算法的执行时间与算法的输入值之间的关系

   def test(num):
       total = 0
       for i in range(num):
           total += 1
       return total
   # 如上面代码，如果把上面的代码体中的代码，第一行代码认为耗时为a，下面的循环，每次循环耗时为b，当前有num个b，返回代码耗时为c。此时这个代码体的总消耗时间为a+(num)b+c。因为a和c都是固定的代码，其中的执行时间是不变的，且耗时极短，基本可以忽略不记。
   # 唯一变化的是循环代码，那么这时候我们就可以认为循环体为整个代码块的运行时间，时间为(num)b，这里我们用O记录，而(num)b可以看成为变量N，所以最后衍生记录为O(N)对时间复杂度的表示
   

2. 时间复杂度表示法和常见时间复杂度案例分析
   常见的时间复杂度
   • O(1)：这个地方认为执行的代码的时间永远不变，其运行时间长度与我们输入的变量是无关的。类似如下代码，不管num如何变化，在代码执行的时候都只运算一次

   def O1(num):
       i = num
       j = num * 2
       return i + j
   

   • O(logN)：如下代码，在while循环体系中，因为循环条件和循环体的特性，这个循环不会被循环num次，而是1x2^n >= num,根据对数公式a^n = b的对数就是n=log(a)(b)得到n=log(2)(num),最后替换为常用字母，小写n代表次数，num换成N，最终得到n=log(N)。1x2^n >= num推导的方法就是，i=1，每次循环都是i=ix2，，写出开头几个运行结果：1x2,1x2x2,1x2x2x2......1x2^n

   def OlogN(num):
       i = 1
       while (i<num):
         i = i * 2
       return i
   

   • O(n)

   def ON(num):
       total = 0
       for i in range(num):
           total += 1
       return total
   

   • O(M+N)：这个其实就是O(N)的一个变体

   def OMN(num1, num2):
       total = 0
       for i in range(num1):
           total += i
       for j in range(num2):
           total += j
       return total
   

   • O(NlogN)：这个是O(N)xO(logN)的变体，把num1看成O(N)，把里面的while看成O(logN)即可

   def ONLogN(num1, num2):
       total = 0
       j = 0
       for i in range(num1):
           while(j < num2):
               total += i + j
               j = j * 2
       return total
   

   • O(N2)：这个有两个O(N)互相嵌套，所以就是O(N2)

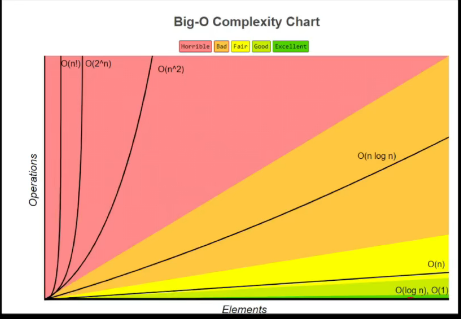
   def ON2(num):
       total = 0
       for i in range(num):
           for j in range(num):
               total += i + j
       return total
   

3. 常见的时间复杂度对比
   O(1)<O(logN)<O(N)<O(NlogN)<O(N^2)<O(2N)<O(N!)
   

空间复杂度

算法的存储空间与输入值之间的关系

1. 空间复杂度O(1)

def test(num):
    total = 0
    for i in range(num):
        total += i
    return total

2. 空间复杂度为O(N)

def test(nums):
    array = []
    for num in nums:
        array.append(num)
    return array

总结

• 如果变量一直是一个类型的常量，则空间复杂度是不变的，如果是一个变量，空间复杂度则不是O(1)
• O(1)<O(N)<O(N^2),一般情况下O(logN)和O(NlogN)不怎么用
• 时间和空间只能二选一，工作中，优先选择时间