几何建模与处理之二 数据拟合（2）

几何建模与处理之二 数据拟合（2）

目录

• 几何建模与处理之二 数据拟合（2）
  • 函数拟合
    • 拟合函数的“好坏”
    • 多项式插值
      • 技巧1：构造插值问题的通用解
      • 技巧2：更方便的求解表达
      • 多项式插值存在的问题
    • 多项式逼近
      • 最小二乘逼近
    • 函数空间及基函数
      • Bernstein多项式做逼近
    • RBF函数插值/逼近
      • Gauss函数
      • RBF函数拟合
      • RBF神经网络
    • 用神经网络函数来拟合数据

回顾：学习了函数、映射、变换等数学上的基础概念和知识，数据拟合的三步曲方法论，四种拟合方法，继续学习函数拟合问题。

函数拟合

输入：一些观察（采用）点\(\lbrace x_i,y_i\rbrace_{i=0}^n\)

输出：拟合数据点的函数\(y=f(x)\)，并用于预测

拟合函数的“好坏”

分段线性插值函数\(y=f_1(x)\)

• 数据误差为0
• 函数性质不好：只有C⁰连续，不光滑（数值计算）

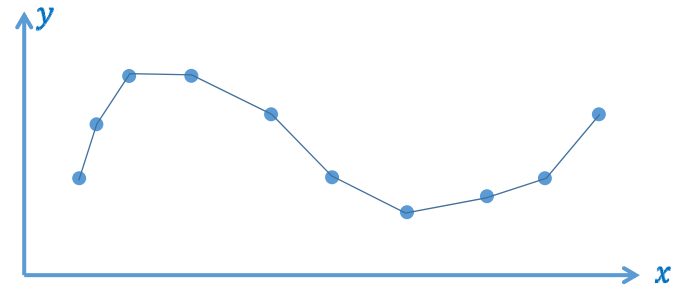
光滑插值函数\(y=f_2(x)\)

• 数据误差为0
• 可能被“差数据”（噪声、outliers）带歪，导致函数性质不好、预测不可靠

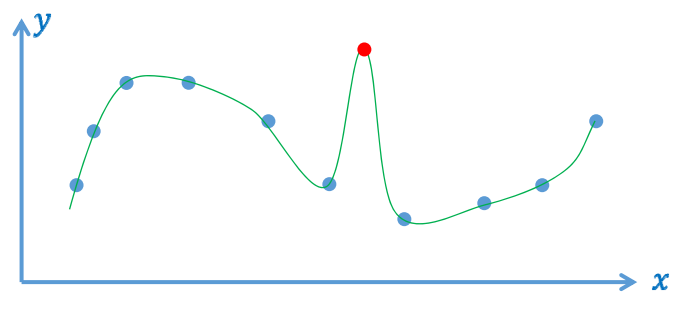
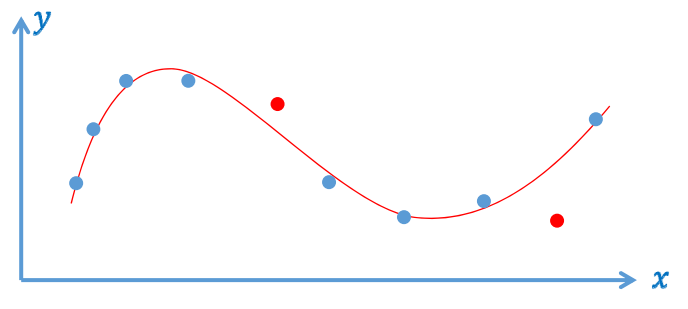
逼近拟合函数\(y=f_3(x)\)

• 数据误差不为0，但足够小

多项式插值

多项式插值定理：若\(x_i\)两两不同，则对于任意给定的\(y_i\)，存在唯一的次数至多是

n次的多项式\(p_n\)，使得\(P_n(x_i)=y_i,i=0,\dots,n\)。

技巧1：构造插值问题的通用解

寻找一组次数为n的多项式基函数\(l_i\)使得

\[l_i(x_j)=\begin{cases} 1,i=j\\0,i\ne j\end{cases} \]

插值问题的解为：

\[P(x)=y_0l_0(x)+y_1l_1(x)+\cdots+y_nl_n(x)=\sum_{i=0}^ny_il_i(x) \]

计算多项式\(l_i(x)\):

\[l_i(x)=C_i(x-x_0)(x-x_i)...(x-x_{i-1})(x-x_{i+1})...(x-x_n)\\=C_i\prod_{j\ne i}(x-x_j)\\ C_i=\frac{1}{\prod_{j\ne i}(x-x_j)} \]

最终多项式基函数（拉格朗日多项式）为

\[l_i(x)=\prod_{j=0,j\ne i}\frac{x-x_j}{x_i-x_j} \]

技巧2：更方便的求解表达

Newton插值：具有相同“导数”（差商）的多项式 构造（n阶Taylor展开）

定义：

一阶差商：

\[f[x_0,x_1]=\frac{f(x_1)-f(x_0)}{x_1-x_0} \]

k阶差商：

\[f[x_0,x_1,\dots,x_k]=\frac{f[x_1,\dots,x_k]-f[x_0,x_1,\dots,x_k]}{x_k-x_0} \]

Newton 插值多项式：

\[N_n(x)=f(x_0)+f[x_0,f_1](x-x_0)+\dots+f[x_0,x_1,\dots,x_k](x-x_0)\cdots(x-x_n-1) \]

多项式插值存在的问题

• 系统矩阵稠密

• 依赖于基函数选取，矩阵可能病态，导致难以求解（求逆）

病态问题：

• 输入数据的细微变化导致输出（解）的剧烈变化

  

• 将线性方程看成直线（超平面）当系统病态时，直线变为近似平行，求解（即直线求交）变得困难、不精确

矩阵条件数：

\[k_2(A)=\frac{\max_{x\ne 0}\frac{||Ax||}{x}}{\min_{x\ne 0}\frac{||Ax||}{x}} \]

• 等于最大特征值和最小特征值之间比例
• 条件数大意味着基元之间有太多相关性

对于等距分布的数据点\(x_i\)，范德蒙矩阵的条件数随着数据点数n呈指数级增长(多项式的最高次数为n -1)

原因：

幂（单项式）函数基：幂函数之间差别随着次数增加而减小；不同幂函数之间唯一差别为增长速度（\(x^i\)比\(x^{x-i}\)增长块）

趋势：

好的基函数一般需要系数交替；互相抵消问题

解决方法：

使用正交多项式基（ Gram‐Schmidt正交化 ）

多项式插值的结果：

• 振荡（龙格Runge）现象；
• 对插值点数高度敏感性

多项式逼近

使用逼近型的好处：

• 数据点含噪声、outliers等
• 更紧凑的表达
• 计算简单、更稳定

最小二乘逼近

\[\mathop{argmin}_{f\in span(B)}\sum_{j=1}^m(f(x_j)-y_j)^2\\ \begin{aligned} \sum_{j=1}^m(f(x_i)-y_j)^2 &=\sum_{j=1}^m(\sum_{i=1}^n\lambda _ib_i(x_j)-y_j)^2\\ &=(M\lambda-y)^T(M\lambda-y)\\ &=\lambda^TM^TM\lambda-y^TM\lambda-\lambda^TM^Ty+y^Ty\\ &=\lambda^TM^TM\lambda-2y^TM\lambda+y^Ty \end{aligned} \]

法方程 最小解满足

\[M^TM\lambda=M^Ty \]

(最小化二次目标函数：\(x^TAx+b^T+c\)，充分必要条件：\(2Ax=-b\))

函数空间及基函数

Bernstein多项式做逼近

伯尔斯坦Bernstein给出了构造性证明。

对[0,1]区间上任意连续函数\(f(x)\)和任意正整数\(n\)，以下不等式对所有\(x\in [0,1]\)成立

\[|f(x)-B_n(f,x)|\lt \frac94m_{f,n}\\ m_{f,n}=\mathop {lower upper bound}_{y_1,y_2\in [0,1]且|y_1-y_2|\lt \frac{1}{\sqrt n}}|f(y_1)-f(y_2)|\\ B_n(f,x)=\sum_{j=0}^nf(x_j)b_{n,j}(x)，其中$x_j$为[0,1]上等距采样点\\ b_{n,j}=\begin {pmatrix} n\\i \end {pmatrix}x_j(1-x)^{n-j} \]

\(b_{n,j}\)为Bernstein多项式。

Bernstein基函数的良好性质：非常好的几何意义！

• 正性、权性（和为1）

• 凸包性

• 变差缩减性

• 递归线性求解方法

• 细分性

• ...

  （在Bezier曲线和B样条篇更详细地学习）

RBF函数插值/逼近

Gauss函数

• 两个参数：均值\(\mu\)，方差\(\sigma\)

  \(g_{\mu, \sigma}(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\)

• 几何意义：

  • 均值\(\mu\)：位置
  • 方差\(\sigma\)：支集宽度

• 不同均值和方差的Gauss函数都线性无关

RBF函数拟合

RBF函数：

\[f(x)=b_0+\sum_{i=1}^nb_ig_i(x) \]

均值\(\mu\)，方差\(\sigma\)对函数的形状影响较大，考虑同时对均值\(\mu\)，方差\(\sigma\)优化。

一般Gauss函数表达为标准Gauss函数的形式：

\[g_{\mu, \sigma}(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}=\frac{1}{\sqrt{2\pi}}e^{-\frac12(\frac x\sigma-\frac \mu \sigma)^2}=g_{0,1}(ax+b)\\ a=\frac 1\sigma,b=-\frac \mu \sigma \]

则RBF函数表达为：

\[f(x)=\omega_0+\sum_{i=1}^n\omega_ig_{0,1}(a_ix+b_i) \]

用标准表达后，基函数是由一个基本函数通过平移和伸缩变换而来的。n足够大，a和b足够多（随机），所产生的函数空间可以逼近所有函数。

将Gauss函数看成网络：

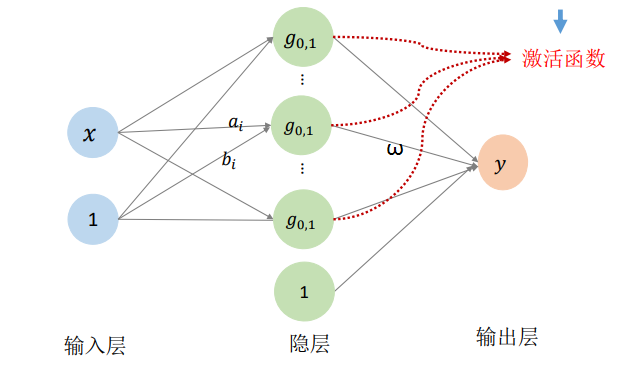
神经元：

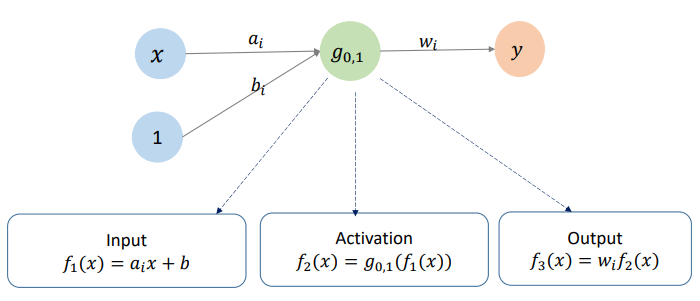
RBF神经网络

• 高维情形：RBF（Radial Basis Function），径向基函数
• 一种特殊的BP网络，优化：BP算法
• 核函数思想
• Gauss函数的特性：拟局部性

启发：由一个简单的函数通过（仿射）变换构造出一组基函数，张成一个函数空间

几种常用的激活函数：

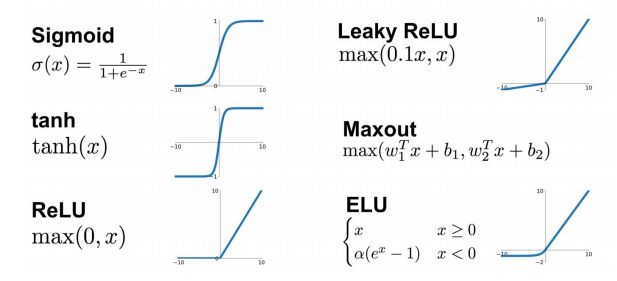
高维情形：多元函数

变量的多个分量的线性组合：

\[(x_1,x_2,\dots,x_n)\to g_{0,1}(a_1^ix_1+a_2^ix_2+\dots+a_n^ix_n+b_i) \]

单隐层神经网络函数：

\[f(x_1,x_2,\dots,x_n)=\omega_0+\sum_{i=1}^nw_ig_{0,1}(a_1^ix_1+a_2^ix_2+\dots+a_n^ix_n+b_i) \]

多层神经网络：多重复合的函数

线性函数和非线性函数的多重复合：

\[h_{W,b}(x)=f(W^Tx)=f(\sum_{i=1}^3W_ix_i+b) \]

\[a_1^{(2)}=f(W_{11}^{(1)}x_1+W_{12}^{(1)}x_2+W_{13}^{(1)}x_3+b_1^{(1)})\\ a_2^{(2)}=f(W_{21}^{(1)}x_1+W_{22}^{(1)}x_2+W_{23}^{(1)}x_3+b_2^{(1)})\\ a_3^{(2)}=f(W_{31}^{(1)}x_1+W_{32}^{(1)}x_2+W_{33}^{(1)}x_3+b_3^{(1)})\\ h_{W,b}(x)=a_1^{(3)}=f(W_{11}^{(2)}a_1^{(2)}+W_{12}^{(2)}a_2^{(2)}+W_{13}^{(2)}a_3^{(2)}+b_1^{(2)}) \]

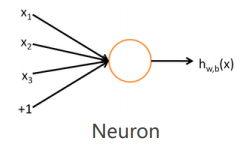
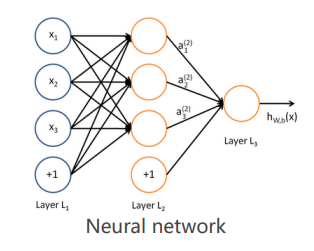
用神经网络函数来拟合数据

理论支撑：万能逼近定理：自由度足够多

问题建模

• 理解问题、问题分解（多个映射级联） …

找哪个？

• 损失函数、各种Penalty、正则项 …

到哪找？

• 神经网络函数、网络简化 …

怎么找？

• 优化方法（BP方法）

• 初始值、参数 …

调参：有耐心、有直觉