[NOI2009]诗人小G
题目描述
小 G 是一个出色的诗人,经常作诗自娱自乐。但是,他一直被一件事情所困扰,那就是诗的排版问题。
一首诗包含了若干个句子,对于一些连续的短句,可以将它们用空格隔开并放在一行中,注意一行中可以放的句子数目是没有限制的。小 G 给每首诗定义了一个行标准长度(行的长度为一行中符号的总个数),他希望排版后每行的长度都和行标准长度相差不远。显然排版时,不应改变原有的句子顺序,并且小 G 不允许把一个句子分在两行或者更多的行内。在满足上面两个条件的情况下,小 G 对于排版中的每行定义了一个不协调度, 为这行的实际长度与行标准长度差值绝对值的 PP 次方,而一个排版的不协调度为所有行不协调度的总和。
小 G 最近又作了几首诗,现在请你对这首诗进行排版,使得排版后的诗尽量协调(即不协调度尽量小),并把排版的结果告诉他。
输入格式
输入文件中的第一行为一个整数 TT,表示诗的数量。
接下来为 TT 首诗,这里一首诗即为一组测试数据。每组测试数据中的第一行为三个由空格分隔的正整数 N,L,PN,L,P,其中:NN 表示这首诗句子的数目,LL 表示这首诗的行标准长度,PP 的含义见问题描述。
从第二行开始,每行为一个句子,句子由英文字母、数字、标点符号等符号组成(ASCII 码 33~12733~127,但不包含 -)。
输出格式
于每组测试数据,若最小的不协调度不超过 10^{18}1018,则第一行为一个数,表示不协调度。接下来若干行,表示你排版之后的诗。注意:在同一行的相邻两个句子之间需要用一个空格分开。
如果有多个可行解,它们的不协调度都是最小值,则输出任意一个解均可。若最小的不协调度超过 10^{18}1018,则输出 Too hard to arrange。每组测试数据结束后输出 --------------------,共20个 -,- 的ASCII码为45,请勿输出多余的空行或者空格。
输入输出样例
4 4 9 3 brysj, hhrhl. yqqlm, gsycl. 4 9 2 brysj, hhrhl. yqqlm, gsycl. 1 1005 6 poet 1 1004 6 poet
108 brysj, hhrhl. yqqlm, gsycl. -------------------- 32 brysj, hhrhl. yqqlm, gsycl. -------------------- Too hard to arrange -------------------- 1000000000000000000 poet --------------------
说明/提示
【样例说明】
前两组输入数据中每行的实际长度均为 66,后两组输入数据每行的实际长度均为 44。一个排版方案中每行相邻两个句子之间的空格也算在这行的长度中(可参见样例中第二组数据)。每行末尾没有空格。
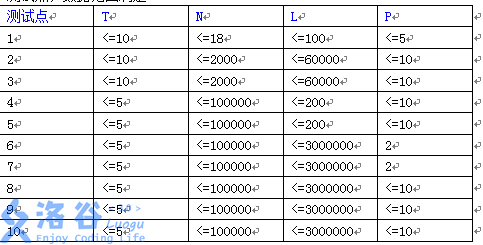
所有句子的长度不超过 30 。
暂时忽略所有字符串方面的操作
首先显然可以得到$O(n^2)$的做法
$f[i]=min(f[j]+|len-l|^p)$
下面考虑使用单调性进行优化
$|len-l|^p$可以视作以l为对称轴的多次函数,显然len的最优决策具有单调性
决策点即为转移方程$f[i]=min(f[j]+|len-l|^p)$中答案最优的$j$
设$F_i$为使i点答案左右的最优决策,那么对于任意$j>i$有$F_j>=F_i$
那么最优决策值构成的数组F(最优决策数组)显然会是这样的形式:
$11112222333.......666$
设$R_i$表示$F_i$作为决策的起始点,即$R_i$之后包括$R_i$都有$i$作为决策点优于$任意j<i$
于是设单调队列,储存$(l,r,x)$表示[l,r)内最优$F_i$为x
转移前将队首满足$r_h<=i$的出队
转移后,分两种情况:
1.使用二分找出对于队尾的三元组的$x_t$的与当前$i$的临界点$S$,如果$S<=l_t$则显然将该区间全部覆盖为i,将队尾出队
2.如果满足$S>l_t$(显然不会大于$r_t$)那么将$(l_t,S,x)$替换队尾
新加入的元素默认$(S,n,i)$,右边界的值会在后面队列操作中修改
本题细节:
1.使用long double,不能使用long long
2.单词间存在空格,输入时可以将单词长度+1(加上空格),l+1(去除行末空格),这样可以直接用前缀和
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 typedef long double ld; 7 ld f[100005],l,p,len[100005]; 8 char w[100005][31]; 9 int q[200005],R[100005],n,pre[100005]; 10 ld qpow(ld x,int k) 11 { 12 ld res=1; 13 while (k) 14 { 15 if (k&1) res=res*x; 16 x=x*x; 17 k>>=1; 18 } 19 return res; 20 } 21 ld Abs(ld x) 22 { 23 if (x<0) return -x; 24 return x; 25 } 26 ld getValue(int x,int y) 27 { 28 return f[y]+qpow(Abs(len[x]-len[y]-l),p); 29 } 30 int binary(int x,int y) 31 { 32 int l=y,r=n+1,mid; 33 while (l<r) 34 { 35 int mid=(l+r)/2; 36 if (getValue(mid,y)>=getValue(mid,x)) r=mid; 37 else l=mid+1; 38 } 39 return l; 40 } 41 int main() 42 {int T,i,flag,j; 43 //freopen("P1912_2.in","r",stdin); 44 //freopen("P1912.out","w",stdout); 45 scanf("%d",&T); 46 while (T--) 47 { 48 scanf("%d%Lf%Lf",&n,&l,&p); 49 l++; 50 for (i=1;i<=n;i++) 51 { 52 scanf("%s",w[i]); 53 len[i]=strlen(w[i]); 54 len[i]+=len[i-1]+1; 55 } 56 int h=1,t=1; 57 q[1]=0;flag=1; 58 for (i=1;i<=n;i++) 59 { 60 while (h<t&&R[h]<=i) h++; 61 f[i]=getValue(i,q[h]); 62 pre[i]=q[h]; 63 if (f[i]>1e18) flag=0; 64 while (h<t&&R[t-1]>=binary(i,q[t])) t--; 65 R[t]=binary(i,q[t]); 66 q[++t]=i; 67 } 68 if (f[n]>1e18) printf("Too hard to arrange\n"); 69 else 70 { 71 t=0;q[0]=n; 72 printf("%.0Lf\n",f[n]); 73 for (i=pre[n];i;i=pre[i]) q[++t]=i; 74 q[++t]=0; 75 for (i=t;i;i--) 76 { 77 for (j=q[i]+1;j<q[i-1];j++) 78 printf("%s ",w[j]); 79 printf("%s\n",w[j]); 80 } 81 } 82 printf("--------------------\n"); 83 } 84 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号