Vofa上位机发送float数据（justfloat协议）

0.小端浮点数

本协议是小端浮点数组形式的字节流协议，纯十六进制浮点传输，节省带宽。此协议非常适合用在通道数量多、发送频率高的时候。

0.0 问题：

发什么?
小端浮点数

什么是小端浮点数？
小端和大端差别在于：字节存储顺序

(以32位float 0x12345678为例）

端序类型	内存地址增长方向（低→高）	实际存储顺序
大端序	`12 34 56 78`	高位字节在前（人类直观顺序）
小端序	`78 56 34 12`	低位字节在前（反向存储）

bf 10 59 3f	//单精度浮点数发送
			//低位字节在前先发

0.1单精度浮点数float（补充，不究原理可以不看）

0.1.1 IEEE-754

IEEE-754（IEEE二进制浮点数算术标准）标准规定了

EEE 754规定了四种表示浮点数值的方式：单精确度（32位）、双精确度（64位）、延伸单精确度（43比特以上，很少使用）与延伸双精确度（79比特以上，通常以80位实现）。

0.1.2 单精度浮点数表示方式

IEEE二进制浮点数算术标准（IEEE 754）是20世纪80年代以来最广泛使用的浮点数运算标准，为许多CPU与浮点运算器所采用。

$$N=(-1)^s \times (1 +{ \frac{M}{2^{23}} }) \times 2^{E-127}$$

$\frac{M}{2^{23}}为小数部分$

例如：

$$（0.0625_{10} = (0.0001)_{2} = (-1)^0 \times (1 + \frac{0}{2^{23}}) \times 2^{123-127}$$

即

$$S = 0 \\M = 0 \\ E = 123$$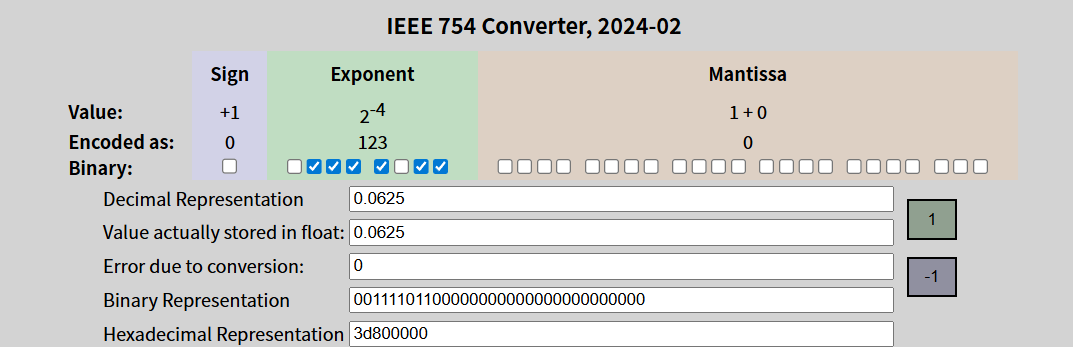

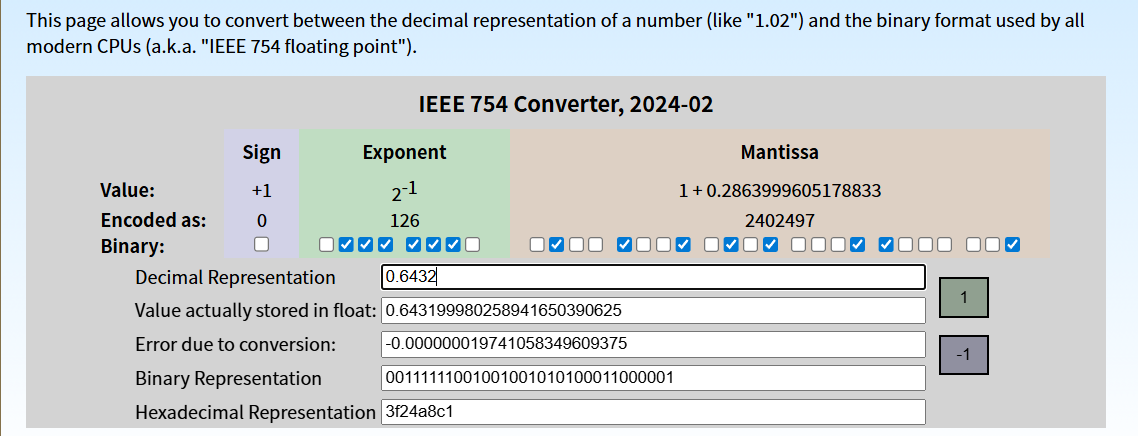
由此，我们明显可以看出，浮点数的表示除了满足2的整数倍之类的情况总是存在误差的。

1. DEMO 程序说明

核心：发送的单精度浮点数转变为4个字节Byte数据发送，每一帧数据后需接包尾 00 00 80 7f

1.1 mid_debug_uart.h

用户数据

//需要添加多少数据，就往enum里加
typedef enum
{
	D1=0,
	D2,
	DATA_COUNT_MAX
}Data_Index;

数据包结构体

typedef struct
{
    float fdata[DATA_COUNT_MAX];
    uint8_t tail[4];
}Vofa_Packet;
extern Vofa_Packet Vofa_packet;

‍

1.2 mid_debug_uart.c

定义发送的数据

Vofa_Packet Vofa_packet;

包尾初始化

/**
 * @brief:	初始化包尾
 * @note:   Must to use Vofa 
 */
void Vofa_Init(Vofa_Packet *frame)
{
    frame->tail[0] = 0x00;
    frame->tail[1] = 0x00;
    frame->tail[2] = 0x80;
    frame->tail[3] = 0x7f;
}

发送浮点数

/**
 * @brief:Vofa_SendFloat
 * @note:
 */
 void Vofa_SendFloat(Vofa_Packet *packet)
 {
    uint8_t byte[4];
    uint8_t i;
    uint32_t temp;
    for(i=0;i<DATA_COUNT_MAX;i++)
    {
        temp = *((uint32_t*)&packet->fdata[i]);  // Reinterpret float as Uint32
        byte[0] = (uint8_t)(temp);
        byte[1] = (uint8_t)(temp >> 8);
        byte[2] = (uint8_t)(temp >> 16);
        byte[3] = (uint8_t)(temp >> 24);
		debug_uart_send_array(byte,4);
    }     
    debug_uart_send_array(packet->tail,4);
 }

发送字节函数（底层）Byte

/**
 * @brief 输入字节(阻塞式发送) hex
 */
void debug_uart_send_byte(uint8_t byte)
{
	while( DL_UART_isBusy(UART_DEBUG_INST) == true );
	DL_UART_Main_transmitData(UART_DEBUG_INST, byte);
}
void debug_uart_send_array(uint8_t *Array,uint8_t length)

{

for(int i=0;i<length;i++)

{

debug_uart_send_byte(Array[i]);

}

}

2.测试

2.1 main.c测试

在main.c函数线初始化数据包

	Vofa_Init(&Vofa_packet);
while (1)
{
	t+=tb;
	if(t&gt;=2*_PI)
	{
		t-=2*_PI;
	}
	Vofa_packet.fdata[D1] = _sin(t);
	Vofa_packet.fdata[D2] = _cos(t);
	Vofa_SendFloat(&amp;Vofa_packet);
	delay_ms(3);
}

在vof上位机中查看波形:

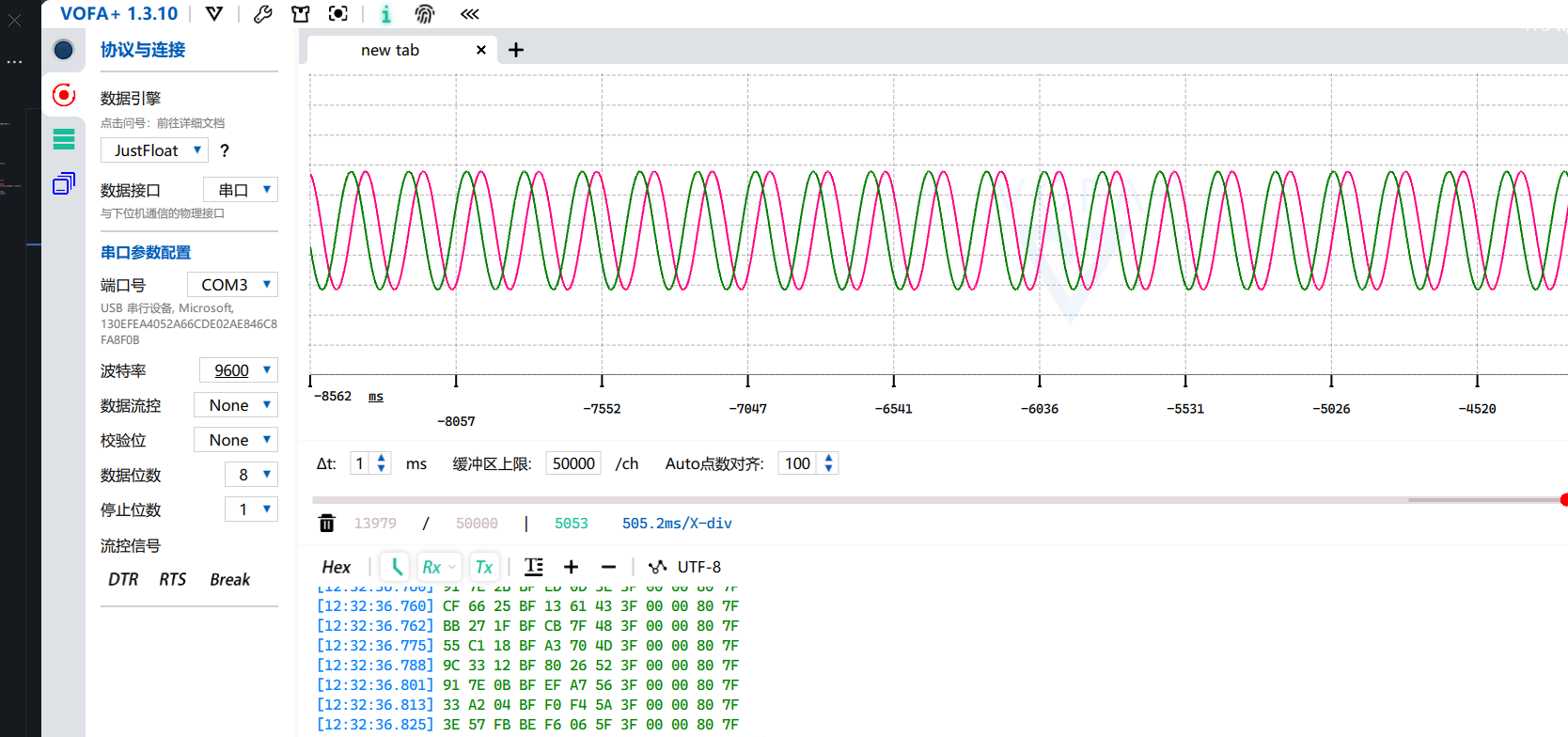
2.2 mid_utils.c

其中_PI、_sin和_cos在我的mid_utils.c和mid_utils.h中，使用查表法来提升正弦运算速度@author:彭志辉

/**
 * @brief:  辅助性函数或工具方法，用于解决常见问题和任务
 * @author: PengZhihui
 * @date:   2025-08-28
 */
include "mid_utils.h"
/**

@brief: 200点正弦波数据，范围0~10000 sin*10000
@note:   int array instead of float array

     2x storage save (int 2Byte float 4 Byte )



     200 points per cycle, 5 cycles per second when timer 1ms



     4x200 points per 360 deg



*/
const int sine_array[200] = {0, 79, 158, 237, 316, 395, 473, 552, 631, 710, 789, 867, 946, 1024, 1103, 1181,

1260, 1338, 1416, 1494, 1572, 1650, 1728, 1806, 1883, 1961, 2038, 2115, 2192,

2269, 2346, 2423, 2499, 2575, 2652, 2728, 2804, 2879, 2955, 3030, 3105, 3180,

3255, 3329, 3404, 3478, 3552, 3625, 3699, 3772, 3845, 3918, 3990, 4063, 4135,

4206, 4278, 4349, 4420, 4491, 4561, 4631, 4701, 4770, 4840, 4909, 4977, 5046,

5113, 5181, 5249, 5316, 5382, 5449, 5515, 5580, 5646, 5711, 5775, 5839, 5903,

5967, 6030, 6093, 6155, 6217, 6279, 6340, 6401, 6461, 6521, 6581, 6640, 6699,

6758, 6815, 6873, 6930, 6987, 7043, 7099, 7154, 7209, 7264, 7318, 7371, 7424,

7477, 7529, 7581, 7632, 7683, 7733, 7783, 7832, 7881, 7930, 7977, 8025, 8072,

8118, 8164, 8209, 8254, 8298, 8342, 8385, 8428, 8470, 8512, 8553, 8594, 8634,

8673, 8712, 8751, 8789, 8826, 8863, 8899, 8935, 8970, 9005, 9039, 9072, 9105,

9138, 9169, 9201, 9231, 9261, 9291, 9320, 9348, 9376, 9403, 9429, 9455, 9481,

9506, 9530, 9554, 9577, 9599, 9621, 9642, 9663, 9683, 9702, 9721, 9739, 9757,

9774, 9790, 9806, 9821, 9836, 9850, 9863, 9876, 9888, 9899, 9910, 9920, 9930,

9939, 9947, 9955, 9962, 9969, 9975, 9980, 9985, 9989, 9992, 9995, 9997, 9999,

10000, 10000};
/**

*@brief:  sine calculation by using fixed size array

*@param a:  angle in between 0 and 2PI

*@note:   ~40us (float array)

~50us (int array)

precision +-0.005

*@note:    126.6873 = 199 / (π/2)

a:(0,π/2) -> (0,199)

*/

float _sin(float a)

{

if (a < _PI_2)

{

return 0.0001f * sine_array[_round(126.6873f * a)];      // int array optimized

}

else if (a < _PI)

{

return 0.0001f * sine_array[398 - _round(126.6873f * a)];     // int array optimized

}

else if (a < _3PI_2)

{

return -0.0001f * sine_array[-398 + _round(126.6873f * a)];      // int array optimized

}

else

{

return -0.0001f * sine_array[796 - _round(126.6873f * a)];      // int array optimized

}

}
float _cos(float a)

{

float a_sin = a + _PI_2;

a_sin = a_sin > _2PI ? a_sin - _2PI : a_sin;

return _sin(a_sin);

}
/**


@brief:square root approximation function using


@note:计算平方根的近似值


https://reprap.org/forum/read.php?147,219210


https://en.wikipedia.org/wiki/Fast_inverse_square_root

*/

float _sqrtApprox(float number)

{//low in fat

long i;

float y;

// float x;

// const float f = 1.5F; // better precision
// x = number * 0.5F;

y = number;

i = (long) &y;

i = 0x5f375a86 - (i >> 1);

y = (float) &i;

// y = y * ( f - ( x * y * y ) ); // better precision

return number * y;

}


/**

@brief:  计算快速平方根倒数（fast inverse square root）
@note:

*/

float FastInvSqrt(float x)

{

float halfx = 0.5f * x;

float y = x;

long i = *(long *)&y;

i = 0x5f3759df - (i >> 1);

y = *(float *)&i;

y = y * (1.5f - (halfx * y * y));

return y;

}

2.3 mid_utlis.h


#ifndef __MID_UTILS_H__
#define __MID_UTILS_H__
// sign function
define _sign(a) ( ( (a) < 0 )  ?  -1   : ( (a) > 0 ) )
define _round(x) ((x)>=0?(long)((x)+0.5f):(long)((x)-0.5f))
define _constrain(amt, low, high) ((amt)<(low)?(low)😦(amt)>(high)?(high):(amt)))
// utility defines
define _2_SQRT3 1.15470053838f
define _SQRT3 1.73205080757f
define _1_SQRT3 0.57735026919f
define _SQRT3_2 0.86602540378f
define _SQRT2 1.41421356237f
define _120_D2R 2.09439510239f
define _PI 3.14159265359f
define _PI_2 1.57079632679f
define _PI_3 1.0471975512f
define _2PI 6.28318530718f
define _3PI_2 4.71238898038f
define _PI_6 0.52359877559f
float _sin(float a);

float _cos(float a);
endif

3.总结和不足

若是纠结发送的数据，可以开启串口DMA降低对系统主频的占用

‍

posted @ 2025-11-22 22:42 Xu_Duoduo 阅读(1) 评论(0) 收藏举报

刷新页面返回顶部

Xuuuduoduo

Vofa上位机发送float数据（justfloat协议）

Vofa上位机发送float数据（justfloat协议）

0.小端浮点数

0.0 问题：

0.1单精度浮点数float（补充，不究原理可以不看）

0.1.1 IEEE-754

0.1.2 单精度浮点数表示方式

1. DEMO 程序说明

1.1 mid_debug_uart.h

1.2 mid_debug_uart.c

2.测试

2.1 main.c测试

2.2 mid_utils.c

include "mid_utils.h"

2.3 mid_utlis.h

define _sign(a) ( ( (a) < 0 ) ? -1 : ( (a) > 0 ) )

define _round(x) ((x)>=0?(long)((x)+0.5f):(long)((x)-0.5f))

define _constrain(amt, low, high) ((amt)<(low)?(low)😦(amt)>(high)?(high):(amt)))

define _2_SQRT3 1.15470053838f

define _SQRT3 1.73205080757f

define _1_SQRT3 0.57735026919f

define _SQRT3_2 0.86602540378f

define _SQRT2 1.41421356237f

define _120_D2R 2.09439510239f

define _PI 3.14159265359f

define _PI_2 1.57079632679f

define _PI_3 1.0471975512f

define _2PI 6.28318530718f

define _3PI_2 4.71238898038f

define _PI_6 0.52359877559f

endif

3.总结和不足

公告