实验三:朴素贝叶斯算法实验
实验三:朴素贝叶斯算法实验
| 姓名 | 许珂 |
| 学号 | 201613344 |
【实验目的】
理解朴素贝叶斯算法原理,掌握朴素贝叶斯算法框架。
【实验内容】
-
针对下表中的数据,编写python程序实现朴素贝叶斯算法(不使用sklearn包),对输入数据进行预测;
-
熟悉sklearn库中的朴素贝叶斯算法,使用sklearn包编写朴素贝叶斯算法程序,对输入数据进行预测;
【实验报告要求】
-
对照实验内容,撰写实验过程、算法及测试结果;
-
代码规范化:命名规则、注释;
-
查阅文献,讨论朴素贝叶斯算法的应用场景。
【实验代码】
一、
1.导入本次实验所需要的包
1 import pandas as pd
2 import numpy as np
3 import json
2.导入数据
1 df = pd.read_excel("D:/py/朴素贝叶斯.xlsx")
2 df

3.对数据进行处理
1 # 导入数据/生成数据表
2 dataSheet = df
3 # print(dataSheet)
4 # 预数据
5 data_proba = {}
6 # 标签/列名称
7 header = dataSheet.columns
8 # 案例个数/行数
9 length = dataSheet.shape[0]
10 # 数据表值
11 values = dataSheet.values
12 # 最后一列的不重复数据
13 end_unique = dataSheet[header[-1]].unique()
14 # 遍历
15 for end in end_unique:
16 # [header[-1]==end]时end出现的次数
17 end_sum = dataSheet[dataSheet[header[-1]].isin([end])].shape[0]
18 # [header[-1]==end]时end出现的频率
19 end_proba = dataSheet[dataSheet[header[-1]].isin([end])].shape[0] / length
20 # 预保存
21 data_proba[end] = {'proba': end_proba, 'data': {}}
22 # 遍历标签/列名称
23 for head in header[:-1]:
24 # 初始化
25 data_proba[end]['data'][head] = {}
26 # 该标签/名称下不重复值
27 head_unique = dataSheet[head].unique()
28 # 遍历属性
29 for head_val in head_unique:
30 # [header[-1]==end]时head_val出现的次数
31 head_val_sum = dataSheet[dataSheet[head].isin([head_val]) & dataSheet[header[-1]].isin([end])].shape[0]
32 # [header[-1]==end]时head_val出现的频率
33 head_val_proba = head_val_sum / end_sum
34 # 预保存
35 data_proba[end]['data'][head][head_val] = head_val_proba
1 print(json.dumps(data_proba, indent=4, ensure_ascii=False))


4.对本次实验进行实验预测
1 # 创建一个存放判断结果的数组
2 new = np.empty((length, 1), str)
3
4 # 遍历values的每一行
5 for val_num in np.arange(length):
6 judge = {}
7 # 遍历最后一列不重复数据
8 for end in end_unique:
9 # 标签/列名称除最后一列的数量
10 header_sum = len(header[:-1])
11 # 创建一个临时存放数据的数组
12 tempor = np.empty(header_sum + 1, float)
13 # 最后一个标签/列名称的属性对应的先验概率
14 end_proba = data_proba[end]['proba']
15 # 加1处理
16 end_proba += 1
17 # 临时保存
18 tempor[-1] = end_proba
19 # 遍历除最后一行的标签/列名称
20 for head_num in np.arange(header_sum):
21 # 标签/列名称
22 head = header[head_num]
23 # 该标签/列名称下的属性
24 val = values[val_num][head_num]
25 # 属性对应的先验概率
26 head_val_proba = data_proba[end]['data'][head][val]
27 # 加1处理
28 head_val_proba += 1
29 # 临时保存
30 tempor[head_num] = head_val_proba
31 # 对数据log处理并求和保存
32 temp = np.log(tempor).sum()
33 judge[temp] = end
34 # 提取后验概率较大的值
35 judge_max = np.max(list(judge.keys()))
36 # 保存预测结果
37 new[val_num] = judge[judge_max]
1 # 将预测结果添加到数据表新列
2 dataSheet['new'] = new
3 # 预测正确的数量
4 rate = dataSheet[dataSheet[header[-1]] == dataSheet['new']].shape[0]
5 # 打印数据表
6 print(dataSheet)
7 # 准确率
8 print('准确率: {rate:.7f}%'.format(rate=100 * rate / length))

二、朴素贝叶斯算法(使用sklearn包),对输入数据进行预测
1.将文字数据化并输出
1 datasets1=[['0','0','0','0','0','0','1'],
2 ['1','0','1','0','0','0','1'],
3 ['1','0','0','0','0','0','1'],
4 ['0','0','1','0','0','0','1'],
5 ['2','0','0','0','0','0','1'],
6 ['0','1','0','0','1','1','1'],
7 ['1','1','0','1','1','1','1'],
8 ['1','1','0','0','1','2','1'],
9 ['1','1','1','1','1','2','0'],
10 ['0','2','2','0','2','1','0'],
11 ['2','2','2','2','2','2','0'],
12 ['2','0','0','2','2','1','0'],
13 ['0','1','0','1','0','2','0'],
14 ['2','1','1','1','0','2','0'],
15 ['1','1','0','0','1','1','0'],
16 ['2','0','0','2','2','2','0'],
17 ['0','0','1','1','1','2','0']
18 ]
19 #青绿:0 乌黑:1 浅白:2
20 # 蜷缩 0 稍蜷 1 硬挺 2
21 # 浊响 0 沉闷 1 清脆 2
22 # 清晰 0 稍糊 1 模糊 2
23 # 凹陷 0 稍凹 1 平坦 2
24 # 碍滑 0 软粘 1 硬滑 2
25 # 是 1 否 0
26 labels = ['色泽','根蒂','敲声','纹理','脐部','触感','好瓜']
27 data1 = pd.DataFrame(datasets1,columns=labels)
28 data1
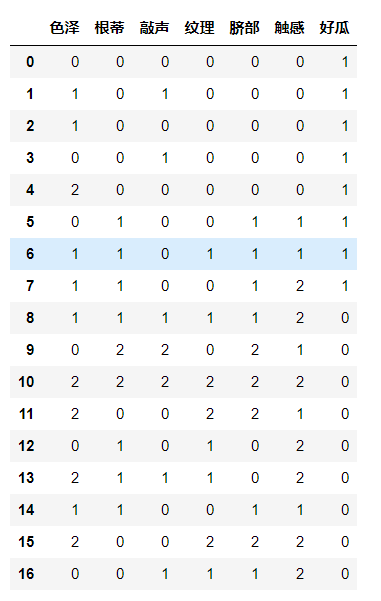
2.数据预测
1 from sklearn.model_selection import train_test_split # 将原始数据划分为数据集与测试集两个部分
2 from sklearn.naive_bayes import BernoulliNB
3
4 X = data1.iloc[:, :-1]
5 y = data1.iloc[:, -1]
6 # X_train训练样本, X_test测试样本, y_train训练样本分类, y_test测试样本分类
7 # X样本数据分类集, y分类结果集, test_size=3测试样本数量,random_state=1 生成数据随机
8 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=3, random_state=None)
9
10 clf = BernoulliNB()
11 clf.fit(X, y)
12 # 返回预测的精确性
13 clf.score(X_test, y_test)
14 # 查看预测结果
15 clf.predict(X_test)
16 # 输入测试样本 ['青绿','蜷缩','浊响','清晰','凹陷','硬滑']
17 tt = ['0', '0', '0', '0', '0', '2']
18 tt = pd.DataFrame(tt)
19 test = tt.T
20 print(clf.predict(test))

三、查阅文献、讨论朴素贝叶斯算法的应用场景
朴素贝叶斯算法的应用场景:
-
-
- 文本分类/垃圾文本过滤/情感判别:即使在现在这种分类器层出不穷的年代,在文本分类场景中,朴素贝叶斯依旧坚挺地占据着一席之地。因为多分类很简单,同时在文本数据中,分布独立这个假设基本是成立的。而垃圾文本过滤(比如垃圾邮件识别)和情感分析(微博上的褒贬情绪)用朴素贝叶斯也通常能取得很好的效果。
- 多分类实时预测对于文本相关的多分类实时预测,它因为上面提到的优点,被广泛应用,简单又高效。
- 推荐系统:朴素贝叶斯和协同过滤是一对好搭档,协同过滤是强相关性,但是泛化能力略弱,朴素贝叶斯和协同过滤一起,能增强推荐的覆盖度和效果。
-


 浙公网安备 33010602011771号
浙公网安备 33010602011771号