20210824K 复盘
看题,发现是原题场,但是不会
t1 发现是很数学的题,绕半天还是只有 \({\cal O}(n)\) 暴力,不懂了,怀疑应该涉及某种科技
扭头去看 t4,发现分块即可,于是动手写 t4,中间犯了智障错误,调了好长时间
扭头去看 t3,写了一个乱搞上去
再去看 t2,哦发现涉及到一些匹配相关内容,但是不剩什么时间了,只好写了个暴力结束
s2oj202. A.完全平方数
确实存在整点计数科技。前置题目是 [HAOI]圆上的整点
"圆上的整点" 给出了这个问题的解决方案:
给定 \(r\),问存在多少整数解 \((a,\ b)\) 使得 \(a^2 + b^ 2 = r^2\)。
其中 \(a,\ b\) 有序,可以为负数
再回头来看这道题。不妨设 \(N = n/2\),那么存在两条限制:
- \(a+b = N\)
- \(ab = k^2\)
解这个方程组,发现 \(a,b\) 一定是 \(\dfrac{N \pm \sqrt{N^2 - (2k)^2}}{2}\) 中的一个。通过分析 \(N\) 是奇数还是偶数不难得出:如果 \(\sqrt{N^2 - (2k)^2}\) 是整数,减出来的结果一定是偶数
所以,只要 \(\sqrt{N^2 - (2k)^2}\) 为整数,那么就唯一对应了一种 \((a,\ b)\) 的无序取值方案
于是统计使得 \(N^2 - (2k)^2 = l^2\) 的 \(k\) 的个数,移项得到:
哦,这就和圆上的整点非常像了。但是还是稍微有点不同的,我们再做分析:
- 首先,圆上的整点中 \((A,\ B)\) 中的任意一个数是可以为负的,所以需要 \(\times 4\),相当于是把 \([0,\ \pi /2)\) 中所有的合法点做水平和垂直对称。 而我们不需要,因为正负在平方之后是无差别的,即,我们只是想统计 \(\sqrt{N^2 - (2k)^ 2}\) 不同的值的个数,而不关心 \(k\) 是正是负之类的。所以不 \(\times 4\)
- 其次,我们要求拆出来的数中一个必须是偶数的平方。那么:
- 如果 \(N\) 是偶数,那么如果 \((2k)^2, l^2\) 都是偶数,没有关系,\(k,\ l\) 是有序的。如果都是奇数?两个奇数平方数之和不可能还是平方数,所以这种情况不可能存在,我们不用考虑它
- 否则,\((2k)^2,\ l^2\) 一定一个奇数一个偶数,我们强制让 \((2k)^2\) 是偶数,那么由有序统计变成无序统计,要 /2。特别的,\((0^2+N^2)\) 这种情况只会被统计一次,我们 -1 之后 /2
s2oj203. B.素数
将每个数看作一个节点,和为素数的两个点之间连边。
显然我们希望对这个图求最大匹配,设为 \(k\)。如果 \(m<k\),那么答案为 \(2m\),否则设 \(s\) 为,所有连边构成的连通块点数。答案为 \(\min(m+k,\ s)\)
容易发现,奇素数一定是有一个偶数 + 一个奇数加起来的
所以说如果没有 2,连出来的图是一个二分图。我们首先忽略 2 在图上跑最大匹配为 \(x\)。
然后,再把所有的 1 都看作是奇数,放在左部点,忽略 1 与 1 的连边,只保留 1 与偶数的连边,跑最大匹配得到 \(y\),说明:我们尽量不用 1,匹配了 x 对,再尽量 1 之间不配对,匹配了 y-x 对,剩下的所有 1 再任意两两配对,总共最大匹配数为
s2oj204. C.广播
分为两种做法:显式建图与非显式建图,但是本质思想是一样的
非显式建图
考虑由根向某点传递信息的过程。对所有可能的树上路径的形态进行讨论,我们发现传播过程中只可能存在这两种路径:
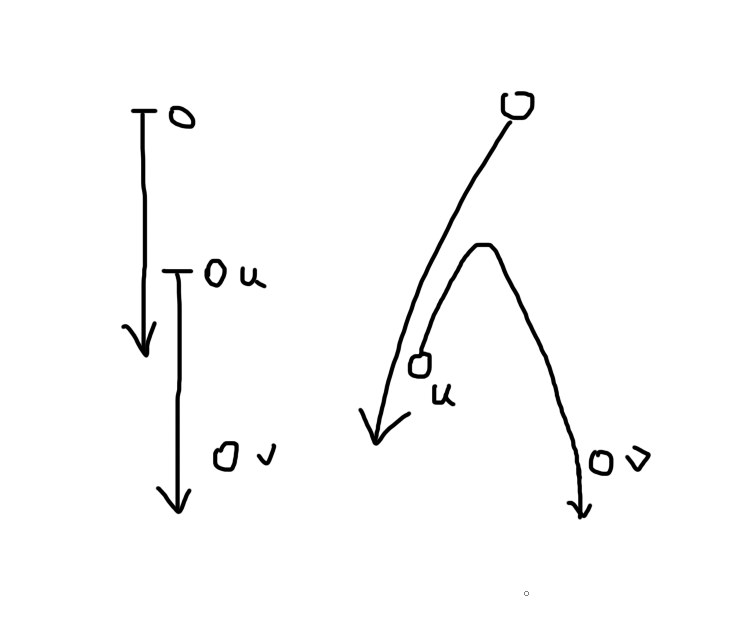
即,层层向下,或者,从 x 传递到 u,u 向上走一段,再向下传递到 v。我们不妨称走到了 u,再走到 v 的这一步称为 u 传播到 v。
那么考虑所有的传播路径,对于一个合法的 u->v 传播路径,我们利用点分治,在该路径的重心处统计到它
具体而言,进行点分治过程,对于每个分治重心,对其所在的连通块进行 bfs,将所有点按照 bfs 序从大到小排序存储(这时你用的是 vector 存储)。同时每个节点存下所有管辖他的分治重心节点编号,即存下点分树父亲。这一步的时间和空间复杂度都是 \({\cal O}(n\log n)\)
点分治过程结束。再进行一遍 bfs,这一遍 bfs 用来求解答案。因为每次传播花费 1 的代价所以选择 bfs
首先 q 里只有 1。然后:
- 取出队头节点 x
- 顺次枚举 x 在点分树上的某个父亲 f 。然后,从 f 所存的 vector 里倒序枚举该重心统辖下的连通块的点(倒序是先取出深度小的)设为 y,如果 x->f 的长度 + f->y 的长度 <= val[x],那么尝试更新 y,如果能更新就把 y push 入 q。pop_back 这个 vector。
就行了
显式建图做法
基本思路一样,但是可能更好理解一点。
只进行一边点分治,不构造点分树。对于每个重心 u,dfs 一遍收集所有连通块节点,设最大的深度为 maxdep。
然后拉一条 maxdep+1 个点的链出来,这些点充当该连通块中每一层所有点的索引。链中由深度大的索引点单向连向深度小的点,边权为 0。然后,枚举每个点 v,由代表其深度的索引点向 v 连边,边权为 0
然后,每个点向索引 val[v] - dep[v] 深度的链上节点连边,边权为 1.表示,我这个点可以跨出 u 的这棵子树传播信息到另一棵子树中 val[v] - dep[v] 及更浅的点。不过需要多花 1 的代价。
上述点分治过程完成,从 1 开始做 01bfs 得到每个点的 dis 就是答案。
s2oj.777. D.【2019FJ省队集训】树
大力分块,预处理 块-点 之间的答案,边角使用欧拉序 \({\cal O}(1)\) 查询两点之间的 dis 即可,复杂度 \({\cal O}(n\sqrt{n}+q\sqrt{n})\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号