20210821K 复盘
看 t1,感觉就很贪心。思考了一个比较复杂的贪心,还是写了
看 t2,哦发现是原题,可能我很久远很久远之前跟着的某次集训里面提到过,二分就行了
看 t3。有一棵方程树,要求支持添加一条边然后询问解的情况,以及修改某点的等式的常数
想到一个大力树剖做法,两个 log 肯定过不去,但是能拿大多数分,于是写了
t4 没时间写暴力了
s2oj749. A.赛
存在一种贪心做法(考场乱贪)
首先按照被喜欢的情况对物品分类,分为:甲乙都喜欢的记为 A,只有甲喜欢的记为 B,只有乙喜欢的记为 C,以及都不喜欢的(没有记号)
我们枚举选多少个 A 类物品,从 0~min(|A|, K) 枚举。那么剩下的一定是要从 B 里面选 K-i 个,从 C 里面选 K-i 个,这样我们就以最小的代价满足限制了。再从 “未被选的 A” 和 “未被选的 B” 和 “未被选的 C” 和 “没人喜欢的物品” 中选价值最少的一些,凑够 m 个物品完事
那么我们用一个小根堆+大根垃圾堆完成,每次新加入物品就塞到小根堆里,优先从小根堆里拿,拿够数量了物品之后再去找垃圾堆,尝试把已选的最大的物品替换为未选的最小的物品,这样不断调整两个堆,就行了
正解:
和上面的开始思路一致。我们枚举 "两个人都喜欢的物品" 被选了 \(i\) 个,然后从 "一个人喜欢" 的物品各拿 \(k-i\) 个,然后剩下再拿一些,剩下要查询前 \(k\) 大的和的话可以用一棵动态开点权值线段树实现。因为 \(i\) 是顺序扫描的,所以只涉及单点操作,在权值线段树上搞一搞就可以了。好像比贪心好想很多
s2oj750. B.Merchant
有很多物品,每个物品是一条直线。容易想到二分一个 t,然后求在 t 时刻前 m 大里面非负数的和
考虑其正确性,我们手玩几种情况发现,这个和只可能单调递增,或者单调递减,或者先减再增
如果在先减后增的函数上二分第一个大于等于 S 的横坐标,左端点会不停的右移
所以只要额外 check(0) 一下就可以应对所有的情况了!
s2oj.751. C.Equation
给出了一棵方程树。我们发现一旦根节点 1 的 \(x\) 值确定下来,其实整棵树也就全确定下来了
那么考虑新加进来的一条边,如果 \(u, v\) 深度奇偶性相同,我们发现 \(x_u+x_v\) 是和 1 的取值无关的,是一个常数恒等式,我们只要判断 \(u,\ v\) 到根的这两个交替和加起来是否等于 s,等于说明有无穷解,否则说明无解
否则,我们一定能根据两个交替和解出来 \(x_1\) 的唯一值,如果这个值是 某.5 则无解,否则有解
考虑如何支持:单点修改,查询某点到根的交错和
倍增不行因为不支持修改,树剖俩 log 只有 86pts
我们可以换一种角度考虑:某点修改影响的是子树,那么为什么不在修改的时候将子树整体加呢?
这样,我们所作的就是一个区间加,单点求值的问题,使用树状数组,区间加就打标记,单点查询的话前缀求和就行了
为啥这么简单的转换没想到呢...
s2oj752. D.Rectangle
考虑 subtask4: 任意两个横坐标不同,纵坐标不同。这样,极小矩形必定两两本质不同。假设我们枚举一个右边界卡着的点 \(i\),枚举一个左边界卡着的点 \(j\),我们只要再找到,横坐标值在 \([x(i),\ x(j)]\) 区间中,纵坐标在 \(\max(y(i),\ y(j))\) 以上的一个点,以及纵坐标在 \(\min(y(i),\ y(j))\) 以下的一个点,就能确定一个本质不同的极小矩形
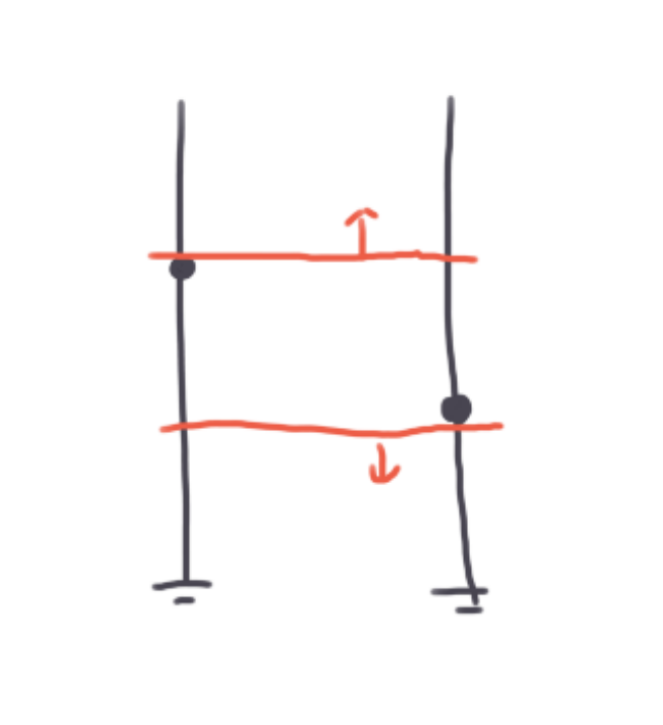
尝试写出来我们想要求的东西,假设 \(\mathbb{U,\ D}\) 是上半和半中点构成的集合,\(L\) 是 \(x(j)\),\(R\) 是 \(x(i)\),那么
那么我们只要求,纵坐标前缀和后缀中点的个数,以及纵坐标值的和即可。此信息可以在 \(j\) 从 \(i\) 向 1 推的过程中用 BIT 实现维护
考虑可重情况
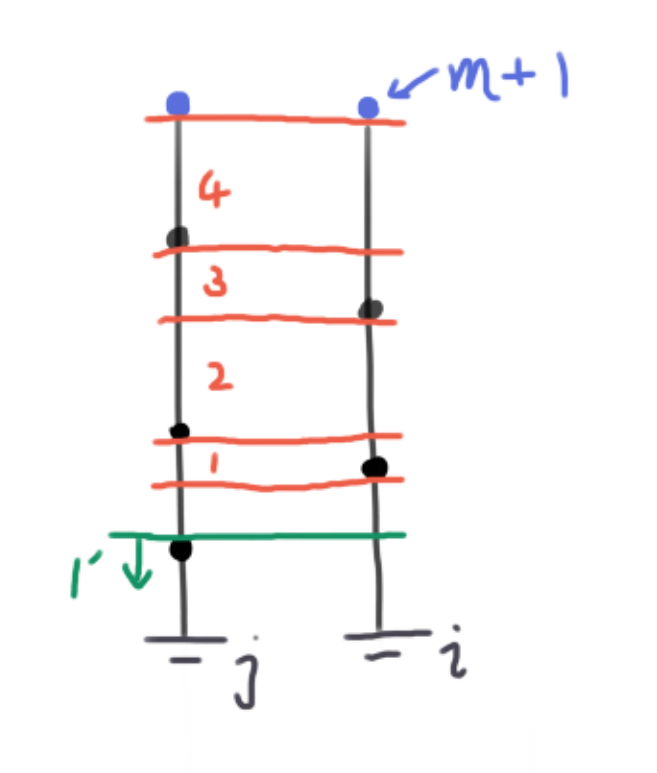
依然枚举右边界横坐标 \(i\),再向左扩展所有可能的左边界横坐标 \(j\)。考虑从下往上依次枚举上界所在的区间
比如上面的情况我们依次枚举 1~4 段,令卡住矩形上边界段的纵坐标落在这个区间里面,然后如果再在下面找一个点,就构成了一个本质不同矩形。换句话说,我们让每一个可能的本质不同的矩形在其 "左右边界上纵坐标最大的点" 构成的点对处被枚举到。
这样就行了。分析复杂度,其实我们做的过程本质上是一个 "枚举点对" 的过程,枚举到 "一段" 其实就是枚举了一个点对,所以总共是 \(n^2\) 枚举的段。每段要在 BIT 上查询,总共复杂度 \({\cal O}(n^2\log n)\)
(实现参考了题解,不参考点代码确实难写)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号