高等代数期中考试
这学期当了高等代数的助教,我出了一份卷子,这周四进行了高等代数期中考试,以下为试题和答案。
问题1(10分)对于线性空间$V$, 若$V=A\oplus B=C\oplus D$, 且$A\subseteq C$, 求证: $$C=A\oplus (B\cap C)$$
问题2(10分)证明: 两个复方阵$\boldsymbol{A},\boldsymbol{B}$相似当且仅当 $\left(\begin{matrix} \boldsymbol{A} \\ & \boldsymbol{A} \end{matrix}\right), \left(\begin{matrix} \boldsymbol{B} \\ & \boldsymbol{B} \end{matrix}\right)$相似.
问题3(10分, Bessel不等式) 对于$\mathbb{R}$-内积空间$V$(不必有限维), 若有限个单位向量$\boldsymbol{e}_1,\ldots,\boldsymbol{e}_n$两两正交, 求证, 对任何$\boldsymbol{x}\in V$, $$\left<\boldsymbol{x},\boldsymbol{x}\right>^2\geq \sum_{i=1}^n |\left<\boldsymbol{x},\boldsymbol{e}_i\right>|^2$$
问题4(20分, Schur)证明: 每个复矩阵$\boldsymbol{A}$都酉相似到上三角形. 具体来说, 存在酉矩阵$\boldsymbol{U}$(即$\boldsymbol{U}^{\mathsf{H}}\boldsymbol{U}=\boldsymbol{E}$, $\{\}^\mathsf{H}$表示共轭转置)和上三角矩阵$\boldsymbol{T}$使得 $$\boldsymbol{A}=\boldsymbol{UTU}^{-1}$$ (提示 :回忆``前Jordan时代''的我们曾经证明的结论---任何一个矩阵都复相似到上三角矩阵. )
问题5(25分)对于$\mathbb{C}$-线性空间$V$, 其上有两个线性变换$\mathscr{A},\mathscr{B}$, 且$\mathscr{A},\mathscr{B}$可交换. 求证: $$\textrm{$\mathscr{A},\mathscr{B}$可对角化}\iff \textrm{$\mathscr{A},\mathscr{B}$可同时对角化}$$ 这里可(同时)对交换的意思是存在一组基, 在这组基下, (两)线性变换对应的矩阵(都)是对角矩阵. 换言之, 存在一组由(公共)特征向量组成的基.
问题6(25分, Jordan分解) 对于有限维$\mathbb{C}$-线性空间$V$, $\mathscr{A}$是其上的线性变换, 本题的目的是为了证明如下的Jordan分解存在且唯一, $$\mathscr{A}=\mathscr{D}+\mathscr{N}$$ 其中$\mathscr{D},\mathscr{N}$都是$V$上的线性变换, 且满足
- $\mathscr{D}$可以对角化. 换言之, 存在一组基$\epsilon_1,\ldots,\epsilon_n$和特征值$\lambda_1,\ldots,\lambda_i$使得$\mathscr{D}\epsilon_i=\lambda_i\epsilon_i$, 对每一个$1\leq i\leq n$. (可对角化条件)
- $\mathscr{N}$是幂零的. 即存在$m>0$使得$\mathscr{N}^m=\mathscr{O}$. (幂零条件)
- $\mathscr{A}$分别与$\mathscr{D}$, $\mathscr{N}$可交换. 即$\mathscr{AD}=\mathscr{DA}, \mathscr{AN}=\mathscr{NA}$. (可交换条件)
本题如果不采用如下过程的思路, 完整地解决亦可得满分(只证明存在性可得5分)
直觉使我们相信$\mathscr{D}$的对角线上应该按重数排列着$\mathscr{A}$的所有特征值, 但是这需要构造和证明. 为此, 假设$\mathscr{A}$的特征多项式为$$f(X)=(X-\lambda_1)^{n_1}\ldots(X-\lambda_k)^{n_k}\qquad \textrm{$\lambda_1,\ldots,\lambda_n\in\mathbb{C}$两两不同}$$ 并且记属于特征值$\lambda_i$的根子空间 $$V_{i}=\ker\left[(\mathscr{A}-\lambda_i)^{n_i}\right]\subseteq V$$
(1)(5分)证明: $V_i$是$\mathscr{A}$-不变子空间.
(2)(5分)证明: $$V=V_1\oplus \ldots \oplus V_k$$ (提示: 只需证明对两个互质的多项式$f,g$有$V=\ker f(\mathscr{A})\oplus \ker g(\mathscr{A})$.)
(3)(5分)证明: 对任意$1\leq j\leq n$, 存在多项式$f_j(X)$使得 $$[f_j(\mathscr{A})](v_1+\ldots+v_k)=v_j\qquad \forall v_i\in V_i$$(提示: 只需要$[f_j(\mathscr{A})](v_i)=v_i$当$i=j$, 而$=0$当$i\neq j$. 用多项式的Béezout定理. )
既然已经构造出$f_j(X)$那么取 $$D(X)=\lambda_1f_1(X)+\ldots+\lambda_kf_k(X)\qquad N(X)=X-D(X)$$ 并令 $$\mathscr{D}=D(\mathscr{A})\qquad \mathscr{N}=N(\mathscr{A})$$
(4)(5分)证明: 如上的$\mathscr{D}, \mathscr{N}$满足Jordan分解的三条要求. 注意到, 此时, $\mathscr{D},\mathscr{N}$甚至还是$\mathscr{A}$的多项式.
(5)(5分, 唯一性)若$\mathscr{D}',\mathscr{N}'$满足Jordan分解的三条要求, 则 $$\mathscr{D}'=\mathscr{D}, \mathscr{N}'=\mathscr{N}$$
在这里你可以使用问题5的结论, 即使你没有解决问题5.
(提示:需要注意到我们构造出的$\mathscr{D}$是$\mathscr{A}$的多项式, 同时注意到两个可以交换的幂零变换的差还是幂零的. )
答案与评注
问题1(10分)对于线性空间$V$, 若$V=A\oplus B=C\oplus D$, 且$A\subseteq C$, 求证: $$C=A\oplus (B\cap C)$$
证明 首先, $A\cap (B\cap C)\subseteq A\cap B=\{0\}$, 故$A\cap B=\{0\}$. 此外, $\forall x\in C\subseteq V$, 则$x=a+b$, 其中$a\in A\subseteq C, b\in B$, 则$b=x-a\in C$, 故$b\in B\cap C$, 故$C=A+(B\cap C)$. 综上所述$C=A\oplus (B\cap C)$. $\square$
评注 找基的方法是错误的! 例如取$A$是$\boldsymbol{e}_1$张成的空间, $C$是$\boldsymbol{e}_1,\boldsymbol{e}_2$张成的空间, $D$是$\boldsymbol{e}_1,\boldsymbol{e}_2, \boldsymbol{e}_3$张成的空间, $B$是$\boldsymbol{e}_1+\boldsymbol{e}_2, \boldsymbol{e}_1+\boldsymbol{e}_3$张成的空间. $\boldsymbol{e}_2,\boldsymbol{e}_3$根本不在$B$里面! 补空间不是唯一的, 在清楚自己写的是什么之前不要使用``的补空间''或者$V/A$的记号. 没有内积结构也不要谈论垂直.
问题2(10分)证明: 两个复方阵$\boldsymbol{A},\boldsymbol{B}$相似当且仅当 $\left(\begin{matrix} \boldsymbol{A} \\ & \boldsymbol{A} \end{matrix}\right), \left(\begin{matrix} \boldsymbol{B} \\ & \boldsymbol{B} \end{matrix}\right)$相似.
证明 必要性显然. 对于充分性, 将$A,B$相似到Jordan标准型$\boldsymbol{J}_A,\boldsymbol{J}_A$, 则$\left(\begin{matrix} \boldsymbol{A} \\ & \boldsymbol{A} \end{matrix}\right), \left(\begin{matrix} \boldsymbol{B} \\ & \boldsymbol{B} \end{matrix}\right)$分别相似于$\left(\begin{matrix} \boldsymbol{J}_A\\ & \boldsymbol{J}_A \end{matrix}\right), \left(\begin{matrix} \boldsymbol{J}_B \\ & \boldsymbol{J}_B \end{matrix}\right)$, 后者也是Jordan标准型, 若$\left(\begin{matrix} \boldsymbol{A} \\ & \boldsymbol{A} \end{matrix}\right), \left(\begin{matrix} \boldsymbol{B} \\ & \boldsymbol{B} \end{matrix}\right)$相似, 则$\left(\begin{matrix} \boldsymbol{J}_A\\ & \boldsymbol{J}_A \end{matrix}\right), \left(\begin{matrix} \boldsymbol{J}_B \\ & \boldsymbol{J}_B \end{matrix}\right)$只相差一些Jordan块的排列, 而$\boldsymbol{J}_A$和$\boldsymbol{J}_B$的Jordan块正是这些Jordan块的一半, 故$\boldsymbol{J}_A$与$\boldsymbol{J}_B$相似. (也可使用初等因子法) $\square$
评注 回归定义是不可能通过分块的方法得到过渡矩阵一定是准对角性! 例如 $$\left(\begin{matrix} 1 \\ & 1 \end{matrix}\right)=\left(\begin{matrix} &1 \\ 1& \end{matrix}\right) \left(\begin{matrix} 1 \\ & 1 \end{matrix}\right)\left(\begin{matrix} &1 \\ 1& \end{matrix}\right)$$
评注 参见李尚志P436. 习题6.
问题3(10分, Bessel不等式) 对于$\mathbb{R}$-内积空间$V$(不必有限维), 若有限个单位向量$\boldsymbol{e}_1,\ldots,\boldsymbol{e}_n$两两正交, 求证, 对任何$\boldsymbol{x}\in V$, $$\left<\boldsymbol{x},\boldsymbol{x}\right>^2\geq \sum_{i=1}^n |\left<\boldsymbol{x},\boldsymbol{e}_i\right>|^2$$
证明 $\left<\boldsymbol{x},\boldsymbol{e}_i\right>$正是$\boldsymbol{x}$在$\boldsymbol{e}_i$上的投影, 受此启发, 作$\boldsymbol{y}=\boldsymbol{x}-\sum_{i=1}^n \left<\boldsymbol{x},\boldsymbol{e}_i\right> \boldsymbol{e}_i$, 此时$\boldsymbol{y}\perp \boldsymbol{e}_i$对任意$1\leq i\leq n$. 故根据勾股定理 $$||\boldsymbol{x}||^2=\left\|\sum_{i=1}^n \left<\boldsymbol{x},\boldsymbol{e}_i\right> \boldsymbol{e}_i\right\|^2+||y||^2\geq \left\|\sum_{i=1}^n \left<\boldsymbol{x},\boldsymbol{e}_i\right> \boldsymbol{e}_i\right\|^2 =\sum_{i=1}^n |\left<\boldsymbol{x},\boldsymbol{e}_i\right>|^2$$ 得证. $\square$
评注 无限维内积空间未必总有单位正交基.
评注 参见李尚志P492. 习题11.
问题4(20分, Schur)证明: 每个复矩阵$\boldsymbol{A}$都酉相似到上三角形. 具体来说, 存在酉矩阵$\boldsymbol{U}$(即$\boldsymbol{U}^{\mathsf{H}}\boldsymbol{U}=\boldsymbol{E}$, $\{\}^\mathsf{H}$表示共轭转置)和上三角矩阵$\boldsymbol{T}$使得 $$\boldsymbol{A}=\boldsymbol{UTU}^{-1}$$ (提示: 回忆``前Jordan时代''的我们曾经证明的结论---任何一个矩阵都复相似到上三角矩阵. )
证明 根据代数基本定理, $\boldsymbol{A}$总有特征向量, 通过单位化, 不妨假设其是单位向量, 将其扩充为全空间的一组单位正交基, 在这组基下$\boldsymbol{A}$的矩阵形如 $$\left(\begin{matrix} \lambda & * \\ 0& \boldsymbol{A}' \end{matrix}\right)$$ 即$\boldsymbol{A}$酉相似到$\left(\begin{matrix} \lambda & * \\ 0& \boldsymbol{A}' \end{matrix}\right)$, 然后利用归纳法得证. (或利用任何矩阵都相似到上三角矩阵(Jordan标准型), 以及QR分解.) $\square$
评注 见李尚志P525 定理9.7.3. 相似和正交相似不一样, 例如 $\boldsymbol{A}=\left(\begin{matrix} 1& 1 \\ & 0 \end{matrix}\right)$相似于$\boldsymbol{B}=\left(\begin{matrix} 1& 0\\ & 0 \end{matrix}\right)$, 但若存在正交矩阵$\boldsymbol{P}$使得$\boldsymbol{P}^T\boldsymbol{A}\boldsymbol{P}=\boldsymbol{B}$, 则 $$\left(\begin{matrix} 1& 0\\ & 0 \end{matrix}\right)= \boldsymbol{B}\boldsymbol{B}^{T}=\boldsymbol{P}^T\boldsymbol{A}\boldsymbol{P}\boldsymbol{P}^T\boldsymbol{A}^{T}\boldsymbol{P}=\boldsymbol{P}^T\boldsymbol{A}\boldsymbol{A}^{T}\boldsymbol{P} =\boldsymbol{P}^T\left(\begin{matrix} 2& 0\\ 0& 0 \end{matrix}\right)\boldsymbol{P}$$ 前者迹为$1$, 后者迹为$2$.
问题5(25分)对于$\mathbb{C}$-线性空间$V$, 其上有两个线性变换$\mathscr{A},\mathscr{B}$, 且$\mathscr{A},\mathscr{B}$可交换. 求证: $$\textrm{$\mathscr{A},\mathscr{B}$可对角化}\iff \textrm{$\mathscr{A},\mathscr{B}$可同时对角化}$$ 这里可(同时)对交换的意思是存在一组基, 在这组基下, (两)线性变换对应的矩阵(都)是对角矩阵. 换言之, 存在一组由(公共)特征向量组成的基.
证明 选定一组基, 转述为矩阵的条件, 假设$\mathscr{A},\mathscr{B}$在这组基下的矩阵是$\boldsymbol{A},\boldsymbol{B}$, 不妨通过选择恰当的基, 假定$\boldsymbol{A}=\left(\begin{matrix}\lambda_1\boldsymbol{E}_1 \\& \ddots \\ && \lambda_k\boldsymbol{E}_k\end{matrix}\right)$, 其中$\lambda_i$互不相同, 对$\boldsymbol{B}$施以同样的分块$\boldsymbol{B}=\left(\begin{matrix}\boldsymbol{B}_{11} & \ldots & \boldsymbol{B}_{1k}\\ \vdots & \ddots& \vdots \\ \boldsymbol{B}_{k1}& \ldots & \boldsymbol{B}_{kk}\end{matrix}\right)$, 验证$\boldsymbol{A}\boldsymbol{B}=\boldsymbol{B}\boldsymbol{A}$得到$\lambda_i\boldsymbol{B}_{ij}=\lambda_{j}\boldsymbol{B}_{ij}$, 因为假定$\lambda_i$两两不同, 故$\boldsymbol{B}_{ij}=\boldsymbol{O}$当$i\neq j$. 故$\boldsymbol{B}=\left(\begin{matrix}\boldsymbol{B}_{11} & \\ &\ddots \\ &&\boldsymbol{B}_{kk}\end{matrix}\right)$, 则因为$\boldsymbol{B}$可对角化, $\boldsymbol{B}_{ii}$也可对角化, 设$\boldsymbol{P}_i$使得$\boldsymbol{P}_i\boldsymbol{B}_{ii}\boldsymbol{P}_i^{-1}$为对角阵, 则$\boldsymbol{P}=\left(\begin{matrix}\boldsymbol{P}_{1} & \\ &\ddots \\ &&\boldsymbol{P}_{k}\end{matrix}\right)$. 则$\boldsymbol{P}\boldsymbol{A}\boldsymbol{P}^{-1}=\boldsymbol{A}$, 且$\boldsymbol{P}\boldsymbol{b}\boldsymbol{P}^{-1}$为对角阵. $\square$
评注 参见李尚志P355. 例4.
问题6(25分, Jordan分解) 对于有限维$\mathbb{C}$-线性空间$V$, $\mathscr{A}$是其上的线性变换, 本题的目的是为了证明如下的Jordan分解存在且唯一, $$\mathscr{A}=\mathscr{D}+\mathscr{N}$$ 其中$\mathscr{D},\mathscr{N}$都是$V$上的线性变换, 且满足
- $\mathscr{D}$可以对角化. 换言之, 存在一组基$\epsilon_1,\ldots,\epsilon_n$和特征值$\lambda_1,\ldots,\lambda_i$使得$\mathscr{D}\epsilon_i=\lambda_i\epsilon_i$, 对每一个$1\leq i\leq n$. (可对角化条件)
- $\mathscr{N}$是幂零的. 即存在$m>0$使得$\mathscr{N}^m=\mathscr{O}$. (幂零条件)
- $\mathscr{A}$分别与$\mathscr{D}$, $\mathscr{N}$可交换. 即$\mathscr{AD}=\mathscr{DA}, \mathscr{AN}=\mathscr{NA}$. (可交换条件)
本题如果不采用如下过程的思路, 完整地解决亦可得满分(只证明存在性可得5分
直觉使我们相信$\mathscr{D}$的对角线上应该按重数排列着$\mathscr{A}$的所有特征值, 但是这需要构造和证明. 为此, 假设$\mathscr{A}$的特征多项式为$$f(X)=(X-\lambda_1)^{n_1}\ldots(X-\lambda_k)^{n_k}\qquad \textrm{$\lambda_1,\ldots,\lambda_n\in\mathbb{C}$两两不同}$$ 并且记属于特征值$\lambda_i$的根子空间 $$V_{i}=\ker\left[(\mathscr{A}-\lambda_i)^{n_i}\right]\subseteq V$$
(1)(5分)证明: $V_i$是$\mathscr{A}$-不变子空间.
(2)(5分)证明: $$V=V_1\oplus \ldots \oplus V_k$$ (提示: 只需证明对两个互质的多项式$f,g$有$V=\ker f(\mathscr{A})\oplus \ker g(\mathscr{A})$.)
(3)(5分)证明: 对任意$1\leq j\leq n$, 存在多项式$f_j(X)$使得 $$[f_j(\mathscr{A})](v_1+\ldots+v_k)=v_j\qquad \forall v_i\in V_i$$(提示: 只需要$[f_j(\mathscr{A})](v_i)=v_i$当$i=j$, 而$=0$当$i\neq j$. 用多项式的Béezout定理. )
既然已经构造出$f_j(X)$那么取 $$D(X)=\lambda_1f_1(X)+\ldots+\lambda_kf_k(X)\qquad N(X)=X-D(X)$$ 并令 $$\mathscr{D}=D(\mathscr{A})\qquad \mathscr{N}=N(\mathscr{A})$$
(4)(5分)证明: 如上的$\mathscr{D}, \mathscr{N}$满足Jordan分解的三条要求. 注意到, 此时, $\mathscr{D},\mathscr{N}$甚至还是$\mathscr{A}$的多项式.
(5)(5分, 唯一性)若$\mathscr{D}',\mathscr{N}'$满足Jordan分解的三条要求, 则 $$\mathscr{D}'=\mathscr{D}, \mathscr{N}'=\mathscr{N}$$
在这里你可以使用问题5的结论, 即使你没有解决问题5.
(提示:需要注意到我们构造出的$\mathscr{D}$是$\mathscr{A}$的多项式, 同时注意到两个可以交换的幂零变换的差还是幂零的. )
证明 (1)任意$\boldsymbol{x}\in \boldsymbol{V}_i$, $$(\mathscr{A}-\lambda_i)^{n_i}\,(\mathscr{A}\boldsymbol{x})=\mathscr{A}(\mathscr{A}-\lambda_i)^{n_i}\boldsymbol{x}=\mathscr{A}0=0$$
(2)首先, 先证明$f,g$互质, 且$fg(\mathscr{A})=\mathscr{O}$时, $V\cong \ker[f(\mathscr{A})]\oplus \ker [g(\mathscr{A})]$. 根据多项式的Béezout定理, 存在$u,v$ 使得 $fu+gv=1$, 则$\forall \boldsymbol{x}\in V$, $\boldsymbol{x}=u(\mathscr{A})f(\mathscr{A})\boldsymbol{x}+v(\mathscr{A})g(\mathscr{A})\boldsymbol{x}$, 且 $g(\mathscr{A})u(\mathscr{A})f(\mathscr{A})\boldsymbol{x}=0, f(\mathscr{A})v(\mathscr{A})g(\mathscr{A})\boldsymbol{x}=0$, 故$V=\ker[f(\mathscr{A})]+\ker [g(\mathscr{A})]$. 若$x\in \ker[f(\mathscr{A})]\cap \ker [g(\mathscr{A})]$, 则$f(\mathscr{A})\boldsymbol{x}=0, g(\mathscr{A})\boldsymbol{x}=0$, 从而 $\boldsymbol{x}=u(\mathscr{A})f(\mathscr{A})\boldsymbol{x}+v(\mathscr{A})g(\mathscr{A})\boldsymbol{x}=0$, 故是直和. 然后, 对于这里, 用于$(X-\lambda_1)^{n_1}$和$f/(X-\lambda_1)^{n_1}$, 然后在子空间$\ker[f/(X-\lambda_1)^{n_1}]$上归纳可得. (也可直接用用$\frac{f(X)}{(X-\lambda_i)^{n_i}}$, 方法是类似的. 但见评注. )
(3)考虑$F_i=\frac{f(X)}{(X-\lambda_i)^{n_i}}$, 他们互质, 利用Béezout定理, 存在$u_i$使得 $\sum_{i=1}^k u_iF_i=1$, 取$f_i=u_iF_i$. 注意到$f_i(\boldsymbol{v}_j)=0$当$i\neq j$时, 故容易验证$f_i(\boldsymbol{v}_j)=v_i$当$i=j$, 而$=0$当$i\neq j$.
(4)每个$i$选$V_i$的一组基, 他们的并还是一组基(因为直和). 且$\mathscr{D}$在每个$V_i$上都是数乘, 从而可对角化. 幂零是因为此时特征值全为$0$, 特征多项式必须是$X^n$. 可以交换是因为是多项式.
(5)假设$\mathscr{A}=\mathscr{D}'+\mathscr{N}'$, 且$\mathscr{A}$与$\mathscr{D}', \mathscr{N}'$交换, 则因为$\mathscr{D}, \mathscr{N}$是$\mathscr{A}$的多项式, $\mathscr{D}, \mathscr{N}$也与$\mathscr{D}', \mathscr{N}'$交换. 则$\mathscr{D}-\mathscr{D}'=\mathscr{N}'-\mathscr{N}$. 假设$\mathscr{N}'^m=\mathscr{O}$, $\mathscr{N}^n=\mathscr{O}$, 因为交换, 所以利用二项式展开可得 $(\mathscr{N}'-\mathscr{N})^{m+n}=\mathscr{O}$, 故也幂零. 而$\mathscr{D},\mathscr{D}'$因为可交换且可以对角化可得可以同时对角化, 因为幂零矩阵特征值都为$0$, 而在某组基下$\mathscr{D}-\mathscr{D}'$是对角阵, 从而$\mathscr{D}=\mathscr{D}'$进而$\mathscr{N}=\mathscr{N}'$. $\square$
评注 $V_1+V_2+V_3=V_1\oplus V_2\oplus V_3$是直和的条件不是两两交$0$! 例如随便在平面上画三条交于$0$的直线.
评注 参见李尚志P436. 习题3.
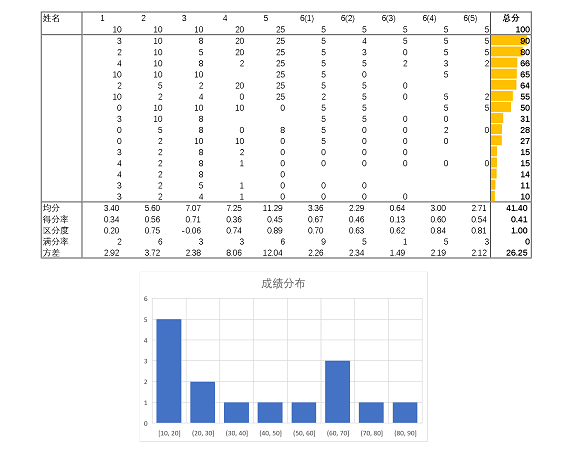
数据分析






 浙公网安备 33010602011771号
浙公网安备 33010602011771号