冒泡排序算法

目录

• 算法原理
  • 原理
  • 流程图
• 算法分析
  • 时间复杂度
  • 算法稳定性
• 算法描述
• 优化

算法原理

原理

• 比较两个相邻的数，如果第一个数大于第二个，则交换他们的位置；
• 对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数；
• 针对所有的元素重复以上的步骤，除了最后一个；
• 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

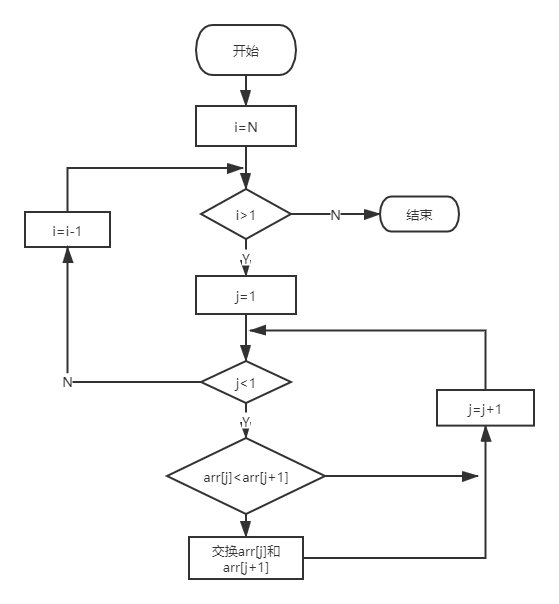
流程图

算法分析

时间复杂度

• 若待排序的文件正好是正序的，那么一次扫面即可完成，比较次数是n-1，交换次数是0，此时冒泡排序的时间复杂度为O(n)；
• 若待排序的文件是反序的，需要进行 趟排序。每趟排序要进行 次关键字的比较(1≤i≤n-1)，且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下，比较和移动次数均达到最大值，此时冒泡排序的最坏时间复杂度为O(n^2)。

算法稳定性

冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较，交换也发生在这两个元素之间。所以，如果两个元素相等，是不会再交换的；如果两个相等的元素没有相邻，那么即使通过前面的两两交换把两个相邻起来，这时候也不会交换，所以相同元素的前后顺序并没有改变，所以冒泡排序是一种稳定排序算法。

算法描述

下面使用java语言对冒泡排序算法作描述：

/**
 * @Description:
 * @Author: 小强
 * @Date: 2021/4/18
 * @Tools: IntelliJ IDEA
 * @Remember: Be professional every day
 **/
public class BubbleSort {
    public static void bubbleSort(int arr[]) {
        //此for循环是需要进行几趟比较
        for (int i = 0; i < arr.length - 1; i++) {
            //此for循环是相邻两数之间比较
            for (int j = 0; j < arr.length - 1 - i; j++) {

                if (arr[j] > arr[j + 1]) {
                    //交换位置
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
    }

    /*
    测试
     */
    public static void main(String[] args) {
        //定义一个待排序的数组
        int[] array = {2, 35, 4, 64, 13, 8, 5, 33, 62, 59, 25};
        //调用bubbleSort冒泡排序算法
        bubbleSort(array);
        //输出排序后的数组
        for (int arr:array) {
            System.out.print(arr+" ");
        }
    }
}

优化

冒泡排序存在一个问题：数据的顺序排好之后，冒泡算法仍然会继续进行下一轮的比较，直到arr.length-1次，后面的比较没有意义的。

优化方案：
设置标志位flag，如果发生了交换flag设置为true；如果没有交换就设置为false。
这样当一轮比较结束后如果flag仍为false，即：这一轮没有发生交换，说明数据的顺序已经排好，没有必要继续进行下去。

优化后的排序算法：

public static void BubbleSort1(int[] arr) {
        int temp;//临时变量

        boolean flag;//是否交换的标志

        for (int i = 0; i < arr.length - 1; i++) {   //表示趟数，一共 arr.length-1 次
            // 每次遍历标志位都要先置为false，才能判断后面的元素是否发生了交换
            flag = false;
            for (int j = arr.length - 1; j > i; j--) { //选出该趟排序的最大值往后移动
                if (arr[j] < arr[j - 1]) {
                    temp = arr[j];
                    arr[j] = arr[j - 1];
                    arr[j - 1] = temp;
                    flag = true;    //只要有发生了交换，flag就置为true
                }
            }
            // 判断标志位是否为false，如果为false，说明后面的元素已经有序，就直接return
            if (!flag) break;
        }
    }