鸽巢原理

鸽巢原理

1.鸽巢原理简单版

Theorem

将 \(n+1\) 个物品放入 \(n\) 个盒子中，至少有一个盒子装入了两个物品。

反证法易证。

Problem A.

一位国际象棋大师有 \(11\) 周的时间备战一场锦标赛。他决定每天至少下一盘棋，且每周最多下 \(12\) 盘棋。

求证：存在连续的若干天，这位大师恰好下了 \(21\) 盘棋。

设 \(s_i\) 为 \(1\sim i\) 天中大师下棋的盘数。那么有 \(1\leq s_1<s_2<s_3<...<s_{76}<s_{77}\leq 132\)。

再构造一个序列：\(22\leq s_1+21<s_2+21<s_3+21<...<s_{77}+21\leq 153\)。

这两个序列中都没有相同的元素。将这两个序列合并，一共有 $154 $ 个数字，但只有 \(153\) 种取值。

所以，一定存在一对 \(i,j\)，使得 \(s_i=s_j+21\)。那么，在第 \([j+1,i]\) 天内，这位大师恰好下了 \(21\) 盘棋。

Problem B.

从 \(1\sim 200\) 这 \(200\) 个整数中任意选取 \(101\) 个。求证：一定存在两个选出的整数，使得其中一个能整除另一个。

我们对于每一个整数，从中拆出尽可能多的 \(2\) 因子。那么，每一个整数都能写成 \(2^k\times t\) 的形式，使得 \(t\) 为奇数。

假设有两个整数 \(2^{k_1} \times t,2^{k_2}\times t\)，它们的 \(t\) 相等。如果 \(k_1>k_2\)，那么第二个数整除第一个；如果 \(k_1<k_2\)，那么第一个数整除第二个。

而 \(1\sim 200\) 中，只有 $100 $ 个奇数。所以选出的 \(101\) 个数字中，至少有一对数字 \(t\) 相同。

Problem C.

给定两个互质的整数 \(n,m\)，以及两个整数 \(a,b\ (a\in[0,n-1],b\in [0,m-1])\)。

求证：存在整数 \(x,p,q\)，使得 \(x=pn+a=qm+b\)。

我们构造这样一个长度为 \(m\) 的序列：\(a,n+a,2n+a,...,(m-2)n+a,(m-1)n+a\)。这个序列中的每一个数字除以 \(n\) 的余数都是 \(a\)。

假设序列中存在两个数模 \(m\) 余数相等。也就是在序列中存在 \(i,j \ (i>j)\) ，使得：

\[\begin{aligned}in+a &\equiv jn+a &\pmod{m}\\(i-j)n &\equiv 0 &\pmod{m}\\m &\mid (i-j)n\end{aligned} \]

因为 \(n\) 与 \(m\) 没有共同的因子，所以 \(i-j\) 是 \(m\) 的倍数。由于 \(i,j\in[0,m-1]\)，那么 \(i-j\in[1,m-1]\)，不可能是 \(m\) 的倍数。这与假设矛盾。

所以序列中的数字模 \(m\) 的结果两两不同，也就意味着 \(0\sim m-1\) 这 \(m\) 个数字都作为余数在序列中出现了一次。

所以，一定存在一个整数 \(pn+a\)，其中 \(p\) 为整数且在 \([0,m-1]\) 之内，模 \(m\) 的余数为 \(b\)。那么这个整数 \(x\) 就满足 \(x=pn+a=qm+b\)。

Problem D.

证明：对于任意的整数 \(a,b \ (b \ne 0)\)，\(\dfrac{a}{b}\) 最终能写成十进制循环小数。

考虑我们是怎么写除法竖式的。求 $\dfrac{a}{b} $ 在十进制下如何表示时，我们先写出 \(\lfloor \dfrac{a}{b} \rfloor\) 这个商，再继续求 \(\dfrac{10\times (a \bmod b)}{b}\) 在十进制下的表示。

如果存在一步，使得 \(b \mid a\)，那么可以视为后面出现了 \(0\) 的循环。

否则，由于 “无限” > \(b\)，那么根据鸽巢原理，一定会存在两步中的 \(a \bmod b\) 的值是相同的，下一步的 \(a\) 也是相同的。于是产生了循环。，

2. 鸽巢原理加强版

Theorem

1. 设 \(n\) 个非负整数 \(c_1,c_2,c_3,...c_n\)。将 \((\sum c_i) + 1\) 个物品放入 \(n\) 个盒子中，一定存在一个盒子 \(i\)，使得装入的物品 \(>c_i\)。
2. 将 \(nm+1\) 个物品放入 \(n\) 个盒子中，至少存在一个盒子装入了 \(>m\) 个物品。
3. 将 \(nm-1\) 个物品放入 \(n\) 个盒子中，至少存在一个盒子装入的物品不足 \(m\)。

Problem A.

现有一个大碟子和一个小碟子，分别被分为了 \(200\) 个扇形。大碟子上的扇形中有 \(100\) 个扇形涂成了红色，另外 \(100\) 个被涂成了蓝色。求证：无论如何给小碟子的扇形染色，总存在一种对齐方案，使得对齐扇形的颜色相同的个数 \(\geq 100\)。

我们总共有 \(200\) 种对齐的方式。而对于小碟子上每一个扇形，无论涂成红色还是蓝色，都有 \(100\) 种与大碟子上颜色相同扇形对齐的方案。

定义一种对齐方案的 “答案” 为对齐扇形的颜色相同的个数。那么我们得到，所有对齐方案的答案之和为 \(200\times 100 =20000\)。

由鸽巢原理，存在一种对齐方案，使得答案 \(\geq \dfrac{20000}{200}=100\)。

Problem B.

设 \(n\) 为整数。现有一个长度为 \(n^2+1\) 的实数序列。求证：要么存在一个长度为 \(n+1\) 的不降子序列，要么存在一个长度为 \(n+1\) 的不升子序列。

原命题等价于：若序列中不存在长度为 \(n+1\) 的不降子序列，那么一定存在长度为 \(n+1\) 的不升子序列。

设 \(l_i\) 为以 \(i\) 开头的不降子序列长度。若序列中不存在长度为 \(n+1\) 的不降子序列，那么对于任意的 \(i\)， \(1\leq l_i\leq n\)。

那么 \(l\) 是由 \(n^2+1\) 个 \([1,n]\) 之内的整数组成的序列。由鸽巢原理，其中至少有 \(n+1\) 个相同的整数。

我们把这 \(n+1\) 个数字拿出来，假设它们为 \(a_{k_1},a_{k_2},...,a_{k_{n+1}}\)。

如果存在一对 \(i,j\)，使得 \(i<j\land a_{k_i} \leq a_{k_j}\)，那么 \(l_{k_i}\) 就会等于 \(l_{k_j}+1\)，矛盾。

所以 \(a_{k_1},a_{k_2},...,a_{k_{n+1}}\) 一定是一个长度为 \(n+1\) 的下降子序列。

3. Ramsey 定理

令 \(K_i\) 表示 \(i\) 阶无向完全图。

Theorem 1

在 \(K_6\) 中，我们用红蓝两种颜色给每条边染色。那么要么存在一个子图 \(K_3\)，使得子图内每条边都是红色，要么存在一个子图 \(K_3\)，使得子图内每条边都是蓝色。

我们记为 \(K_6 \rightarrow K_3,K_3\)。

我们把其中一个点 \(x\) 拿出来，它一定有 \(5\) 个邻居。 根据鸽巢原理，一定至少有 \(3\) 条邻边颜色相同。

我们把这 \(3\) 个邻居拿出来。如果这 \(3\) 条出边都是红色。如果这 \(3\) 个点中存在红色边，那么我们找到了一个红 \(K_3\)。否则，这 \(3\) 个点构成了一个蓝 \(K_3\)。如果这 \(3\) 条边都是蓝色，同上可证。

Theorem 2

我们令 \(K_p\rightarrow K_n,K_m\) 表示用红蓝两种颜色给 \(p\) 阶完全图的每条边染色，要么存在一个红 \(K_n\)，要么存在一个蓝 \(K_m\)。

设 Ramsey 数 \(r(n,m)\)，表示使得 \(K_p \rightarrow K_n,K_m\) 最小的整数 \(p\)。

我们有 \(r(3,3)=6\)。

定理 1 中的证明已经给出了 \(r(3,3)\leq 6\) 的证明。接下来证明 \(r(3,3)\geq 6\)。

我们存在一种给 \(K_5\) 染色的方法，使得其中不存在同色 $ K_3$。

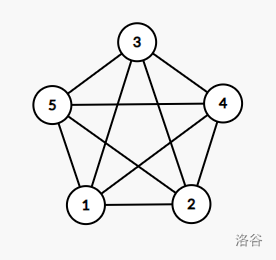
考虑以下构造：我们把 \((1,2),(2,4),(4,3),(3,5),(5,1)\) 这样一圈染成红色，里面的点染成蓝色。

类似地，我们可以证明 \(r(3,4) \leq 10\)。

我们在 \(K_{10}\) 中随意取出一个点 \(x\)。设与 \(x\) 相连的红色边数量为 \(m\)，蓝色边数量为 \(n\)。分两种情况讨论：

• \(m\geq 4\)。若这些由红色边连接的点中存在红色边，那么我们找到一个红 \(K_3\)；否则找到一个蓝 \(K_4\)。
• \(m\leq 3\)，此时 \(n \geq 6\)。由 \(r(3,3)=6\)，在这些由蓝色边连接的点中如果存在红 \(K_3\)，那么结束；否则存在一个蓝 \(K_3\)，它与 \(x\) 组成了一个蓝 \(K_4\)。

Theorem 3

对于任意的正整数 \(n,m\)，若 \(n\geq 2,m\geq 2\)，则存在 \(r(n,m)\)。

首先我们有 \(r(2,n)=r(n,2)=n\)。证明略去。

数学归纳法，\(\min(n,m)=2\) 时显然存在。假设 \(r(n-1,m),r(n,m-1)\) 存在，接下来证明 \(r(n,m)\) 也存在。

设 $ p=r(n-1,m)+r(n,m-1) $。在 \(K_p\) 中，我们拿出一个点 \(x\)，那么它有 \(p-1\) 个邻居和 \(p-1\) 条出边。

根据鸽巢原理，在这些出边中，要么红色边连接的点数量 \(\geq r(n-1,m)\)，要么蓝色边连接的点数量 \(\geq r(n-1,m)\)。

如果红色边连接的点数量 \(\geq r(n-1,m)\)，那么我们在这些点中如果出现蓝 \(K_m\)，那么结束；否则一定存在一个红 \(K_{n-1}\)，它们与 \(x\) 构成了一个红 \(K_n\)。

如果蓝色边连接的点数量 \(\geq r(n-1,m)\)，可以得到相同的结论。

那么我们有：对于任意的正整数 \(n,m\)，存在 \(r(n,m)\)，且 \(r(n,m)\leq r(n-1,m)+r(n,m-1)\)。

Theorem 4

\(r(3,3,3)=17\)。把 \(K_{17}\) 中的边任意染成红、绿、蓝中的一种颜色，一定会出现一个同色 $K_3 $。

首先考虑证明 \(r(3,3,3)\leq 17\)。

我们把 \(K_{17}\) 中拿出一个点 \(x\)，那么它有 \(16\) 条出边和 \(16\) 个邻居。

根据鸽巢原理，一定存在 \(\geq 6\) 条颜色相同的出边。

我们把这 \(6\) 条出边拿出来，假设其为红色。如果这 \(6\) 个点之间有红色边，那么出现了一个红 \(K_3\)；否则，由于 \(r(3,3)=6\)，那么在这 \(6\) 个点中一定存在一个蓝 \(K_3\) 或绿 \(K_3\)。

与鸽巢原理

Ramsey 定理有更一般的形式：

• 令 \(K_{p}^t\rightarrow K_{q_1}^t,K_{q_2}^t,K_{q_3}^t,...,K_{q_n}^t\) 表示给大小为 \(p\) 的集合的每个 \(t\) 元素子集染成 \(c_1,c_2,c_3,...c_n\) 这 \(n\) 中颜色的一种，那么存在一个 \(1 \leq i \leq n\)，使得存在一个 \(q_i\) 元素子集 \(S\)，\(S\) 的每个 \(t\) 元素子集都被染成了颜色 \(c_i\)。
• 设 \(r_t(q_1,q_2,q_3,...q_n)\) 为使得 \(K_{p}^t\rightarrow K_{q_1}^t,K_{q_2}^t,K_{q_3}^t,...,K_{q_n}^t\) 的最小正整数。对于 \(1 \leq t \leq q_i\)，\(r_t(q_1,q_2,q_3,...q_n)\) 总存在。

当 \(t=2\) 时，我们把 \(2\) 元素子集看做边，那么就对应了上面的完全图。

当 \(t=1\) 时，\(r_1(q_1,q_2,q_3,...,q_n)\) 为：

• 最小的整数 \(p\)，使得给大小为 \(p\) 的集合染成 \(c_1,c_2,c_3,...c_n\) 这 \(n\) 种元素的一种，总存在一个 \(1\leq i \leq n\)，至少有 \(q_i\) 个元素被染成了颜色 \(c_i\)。

那么根据鸽巢原理，\(r_1(q_1,q_2,q_3,...q_n)=(\sum q_i)-n+1\)。

这就说明，Ramsey 定理是鸽巢原理加强版的进一步扩展。