组合数学-二项式系数

组合数学-二项式系数

1. 帕斯卡公式

\[\binom{n}{m}=\binom{n-1}{m}+\binom{n-1}{m-1} \]

分两种情况：

• 在前 \(n-1\) 个中已经选出 \(m\) 个；
• 在前 \(n-1\) 个中选出 \(m-1\) 个，加上刚刚选的第 \(m\) 个。

可用于 \(O(n^2)\) 预处理组合数。

2. 组合恒等式

i.吸收恒等式

\[\binom{n}{m}=\frac{n}{m}\binom{n-1}{m-1} \]

• Proof：

\[\begin{aligned}\frac{n}{m} \binom{n-1}{m-1} &=\dfrac{n}{m} \times \dfrac{(n-1)!}{(m-1)!(n-m)!}\\&= \dfrac{n!}{m!(n-m)!}\\&= \binom{n}{m}\end{aligned} \]

同理可得：

\[\binom{n}{m}=\dfrac{n}{n-m} \times \binom{n-1}{m} \]

\[\binom{n}{m}=\dfrac{n-m+1}{m} \times \binom{n}{m-1} \]

ii.对称恒等式

\[\binom{n}{m}=\binom{n}{n-m} \]

组合意义：\(n\) 选 \(m\)，相当于 \(n\) 个中不选 \(n-m\) 个。

iii.上指标求和1

\[\sum_{i=0}^n \binom{m+i}{m}=\binom{n+m+1}{m+1} \]

• Proof
  \[\begin{aligned}\sum_{i=0}^n \binom{m+i}{m} &= \binom{m}{m} +\binom{m+1}{m} + \dots + \binom{m+n}{m} \\&= \binom{m+1}{m+1} + \binom{m+1}{m} + \binom{m+2}{m} + \dots + \binom{m+n}{m}\\ &= \binom{m+2}{m+1} + \binom{m+2}{m} + \dots + \binom{m+n}{m} \\&= \binom{m+3}{m+1} + \binom{m+3}{m} + \dots + \binom{m+n}{m} \\&= \binom{m+n+1}{m+1}\end{aligned} \]

iv.上指标求和2

\[\sum_{i=k}^{n} \binom{i}{k}=\binom{n+1}{k+1} \]

组合意义：考虑 \(n+1\) 个物品中选 \(k+1\) 个，若最后一个选出的物品是第 \(i\) 个，那么前面选择方案有 \(\binom{i-1}{k}\) 种。

v.对角线求和

\[\sum_{i=0}^{m}\binom{n+i}{i} =\sum_{i=0}^{m}\binom{n+i}{n}=\binom{n+m+1}{n+1} \]

利用对称恒等式转化为上指标求和 1。

vi.组合数前缀和

设 \(S_{n,m}=\sum_{i=0}^{m} \binom{n}{i}\)。有递推：

\[S_{n,m}=S_{n,m-1}+\binom{n}{m}=S_{n,m+1}-\binom{n}{m+1} \]

\[S_{n,m}=\sum_{i=0}^m\binom{n}{i}=\sum_{i=0}^m\binom{n-1}{i}+\sum_{i=0}^m\binom{n-1}{i-1}=2S_{n-1,m}-\binom{n-1}{m} \]

\[S_{n,m}=\dfrac{S_{n+1,m}+\binom{n}{m}}{2} \]

vii.范德蒙德卷积

\[\sum_i \binom{n}{i}\binom{m}{k-i}=\binom{n+m}{k} \]

从 \(A\) 集合选出 \(x\) 个，从 \(B\) 集合选出 \(y\) 个，当 \(x+y\) 为定值时可套用。

若 \(x-y\) 为定值，转化为在 \(B\) 集合中不选 \(m-y\) 个，那么 \(x+m-y\) 为定值，得到 \(\binom{n+m}{x+m-y}\)。

viii.格路计数

从 \((0,0)\) 向下、向右走到 \((n,m)\) 的方案数为 \(\binom{n+m}{n}\)。

组合意义：总共要走 \(n+m\) 格， \(n\) 格向下，\(m\) 格向右。在 $n+m $ 步中选择 \(n\) 步向下走。

3. 二项式定理

Theorem

\[(a+b)^n = \binom{n}{0}a^0b^n + \binom{n}{1}a^1b^{n-1} + \binom{n}{2} a^2b^{n-2} + \dots + \binom{n}{n-1}a^{n-1}b^1 + \binom{n}{n}a^nb^0 = \sum\limits_{i=0}^n \binom{n}{i}a^ib^{n-i} \]

组合意义：将原式全部拆开，对于 \(a^ib^{n-i}\) 项，在拆开后的式子中出现了 \(\binom{n}{i}\) 次。

代数推导：数学归纳法。当 \(n=1\) 时显然成立。当 \(n>1\) 时，假设 \(n-1\) 成立，则：

\[\begin{aligned} (a+b)^n &=(a+b)(a+b)^{n-1} \\ &= (a+b) \sum_{i=0}^{n-1} \binom{n-1}{i} a^ib^{n-i-1}\\ &= a\sum_{i=0}^{n-1} \binom{n-1}{i} a^ib^{n-i-1}+b\sum_{i=0}^{n-1} \binom{n-1}{i} a^ib^{n-i-1}\\ &=\sum_{i=0}^{n-1} \binom{n-1}{i} a^{i+1}b^{n-i-1}+\sum_{i=0}^{n-1} \binom{n-1}{i} a^ib^{n-i}\\ &=\sum_{i=1}^{n}\binom{n-1}{i-1}a^ib^{n-i}+\sum_{i=0}^{n-1} \binom{n-1}{i} a^ib^{n-i}\\ &=a^n+\sum_{i=1}^{n-1}\binom{n-1}{i-1}a^ib^{n-i}+b^n+\sum_{i=1}^{n-1} \binom{n-1}{i} a^ib^{n-i}\\ &=\sum_{i=1}^{n-1}(\binom{n-1}{i-1}+\binom{n-1}{i})a^ib^{n-i}+a^n+b^n\\ &=\sum_{i=1}^{n-1}\binom{n}{i}a^ib^{n-i} +\binom{n}{n}a^n+\binom{n}{0}b^n\\ &=\sum\limits_{i=0}^n \binom{n}{i}a^ib^{n-i} \end{aligned} \]

i.下指标求和1

\[\sum_{i=0}^n\binom{n}{i}=2^n \]

组合意义：设 \(S={1,2,3,...,n}\)，\(S_i\) 为 \(S\) 大小为 \(i\) 的子集的集合。所有 $S_i $ 的并集是 \(S\)，且两两不交。

代数意义：二项式定理，\((1+1)^n\)。

ii.下指标交错和

\[\sum_{i=0}^n(-1)^i\binom{n}{i}=0 \]

代数意义：原式化为 \((1-1)^n\)。

组合意义：在 \(n\) 个物品中选择奇数个物品的方案等于选择偶数个物品的方案。假设我们要选取偶数个物品，前 \(n-1\) 个物品可以任选。如果已经选出了偶数个物品，那么第 \(n\) 个不选；如果已经选择了奇数个，那么第 \(n\) 个必须选，则总方案数为 \(2^{n-1}\)。要选取奇数个物品也是同理的，总方案数也是 \(2^{n-1}\)。

iii.下指标求和2

\[\sum_{i=1}^n \binom{n}{i}i=n \times 2^{n-1} \]

代数推导：

\[\begin{aligned} \sum_{i=1}^n \binom{n}{i}i &= \sum_{i=1}^n \binom{n-1}{i-1}\dfrac{n}{i} \times i \\ &=n\sum_{i=1}^n \binom{n-1}{i-1} \\ &= n \sum_{i=0}^{n-1} \binom{n-1}{i}\\ &= n \times 2^{n-1} \end{aligned} \]

4. 不定方程整数解问题

Problem A.

现有 \(k\) 个未知数 \(x_1,x_2,x_3,...x_k\)，求不定方程 正整数解 的个数：\(\sum x_i=n\)。

我们假设现在有 \(n\) 个物品排成一排，每两个物品中间都有一个空当，共有 $n-1 $ 个空当。

若要把这 \(n\) 个物品分成 \(k\) 部分，那么我们需要插入 \(k-1\) 个 “隔板”，共有 \(\binom{n-1}{k-1}\) 种方案。

对于每一种方案，我们就令 \(x_i\) 为分出的第 \(i\) 个部分中物品个数，可以唯一对应一种合法的解。

对于每一组解，我们令第 \(i\) 个部分中物品个数为 \(x_i\)，可以唯一对应一种插隔板的方案。

则解的个数就是插板方案数，即 \(\binom{n-1}{k-1}\)。

Problem B.

现有 \(k\) 个未知数 \(x_1,x_2,x_3,...x_k\)，求不定方程 非负整数解 的个数：\(\sum x_i=n\)。

令 \(y_i=x_i+1\)，那么 \(\sum y_i=n+k\).。此时 \(y_i\) 一定为正整数。

\(y_i\) 的合法解，能够与 \(x_i\) 的合法解一一对应。由上面的叙述，可知 $y_i $ 解的个数为 \(\binom{n+k-1}{k-1}\)，那么原问题的答案也是 \(\binom{n+k-1}{k-1}\)。

5. 多重集合的排列与组合

首先引入多重集合的概念：

• 确定的、无序的、可重的集合。

由 \(1\) 个 \(x\)，\(3\) 个 \(y\)，\(5\) 个 \(z\) 组成的多重集合可表示为 \(\{ 1\cdot x,3 \cdot y,5\cdot z \}\)。

Problem A.

现有一个多重集合 \(S=\{c_1\cdot x_1,c_2\cdot x_2,...c_k\cdot x_k\}\)，\(\sum c_i=n\)。

我们任意地取出 \(S\) 的每一个元素排成一个序列，问会形成多少种不同的序列？

首先我们拿出 \(c_1\) 个 \(x_1\)，有 \(\binom{n}{c_1}\) 种安排位置的方案。

再拿出 \(c_2\) 个 \(x_2\)，有 \(\binom{n-c_1}{c_2}\) 种安排位置的方案。

依次进行下去，最后的答案即为：

\[\binom{n}{c_1}\binom{n-c_1}{c_2}\binom{n-c_1-c_2}{c_3}\cdots \binom{c_k}{c_k}=\dfrac{n!}{c_1!c_2!c_3!\cdots c_k!} \]

展开二项式系数，进行约分即可。

Problem B.

现有一个多重集合 \(S=\{\infty\cdot x_1,\infty\cdot x_2,...\infty\cdot x_k\}\)。

我们任意地取出 \(S\) 的 \(m\) 个元素生成一个集合，问会形成多少种不同的集合？

问题转化为不定方程非负整数解问题：\(\sum x_i=m\) 的解个数。

答案就是 \(\binom{k+m-1}{k-1}\)。

6. 二项式系数的单峰性

我们把 \(\binom{n}{0},\binom{n}{1},\binom{n}{2},\cdots,\binom{n}{n}\) 排成一个序列。那么存在一个 \(t\)，使得 \(1\sim t\) 不降，\(t\sim n\) 不升。

进一步地，若 \(n\) 为奇数，则 \(t=\lceil\dfrac{n}{2} \rceil\)，否则 \(t=\dfrac{n}{2}\) 或 \(\dfrac{n}{2}+1\)。

我们把 \(\binom{n}{k},\binom{n}{k-1}\) 拿出来作商，有：

\[\dfrac{\binom{n}{k}}{\binom{n}{k-1}}=\dfrac{\dfrac{n!}{k!(n-k)!}}{\dfrac{n!}{(k-1)!(n-k+1)!}}=\dfrac{n-k+1}{k} \]

若 \(n-k+1<k\)，则 \(k<\dfrac{n}{2}\)；

若 \(n-k+1=k\)，则 \(k=\dfrac{n}{2}\)；

若 \(n-k+1>k\)，则 \(k>\dfrac{n}{2}\)。

讨论一下 \(n\) 的奇偶即可。

7. 多项式系数

我们把二项式系数扩展到多项式系数：\(\binom{n}{c_1 \ c_2\ c_3 \cdots \ c_k}\) 表示把 \(n\) 个物品划分为 \(k\) 个集合，使得第 \(i\) 个集合大小为 \(c_i\) 的方案数。

我们有：

\[\binom{n}{c_1 \ c_2\ c_3 \cdots \ c_k}=\binom{n}{c_1}\binom{n-c_1}{c_2}\binom{n-c_1-c_2}{c_3}\cdots \binom{n-\sum_{i=1}^{k-1}c_i}{c_k}=\dfrac{n!}{c_1!c_2!c_3!\cdots c_k!} \]

注意到它的值与 5.B 中多重集合排列问题的答案相等。

对于一种分割方案，我们考虑一个长度为 \(n\) 的序列 \(A\)，把所有第 \(i\) 个集合中的元素 \(x_j\) 拿出来，并令 \(A_{x_j}\) 等于 \(i\)。这样一种分割方案能够唯一对应一个多重集合的排列方案。

对于一种排列方案，我们把 \(A_i=j\) 的所有 \(i\) 全部放入 \(j\) 集合中，那么一种排列方案就唯一对应一种分割方案。

帕斯卡公式

\[\binom{n}{c_1 \ c_2\ c_3 \cdots \ c_k}=\binom{n-1}{c_1-1 \ c_2\ c_3 \cdots \ c_k}+\binom{n-1}{c_1 \ c_2-1\ c_3 \cdots \ c_k}+\cdots + \binom{n-1}{c_1 \ c_2\ c_3 \cdots \ c_k-1} \]

组合意义：考虑第 \(n\) 个物品被分入了哪一个集合，加法原理即可。

代数推导：

\[\begin{aligned}& \quad \binom{n-1}{c_1-1 \ c_2\ c_3 \cdots \ c_k}+\binom{n-1}{c_1 \ c_2-1\ c_3 \cdots \ c_k}+\cdots + \binom{n-1}{c_1 \ c_2\ c_3 \cdots \ c_k-1} \\&= \dfrac{(n-1)!}{(c_1-1)!c_2!c_3!\cdots c_k!}+\dfrac{(n-1)!}{c_1!(c_2-1)!c_3!\cdots c_k!}+\cdots+\dfrac{(n-1)!}{c_1!c_2!c_3!\cdots (c_k-1)!}\\&=\dfrac{n!}{c_1!c_2!c_3!\cdots c_k!}\dfrac{c_1}{n}+\dfrac{n!}{c_1!c_2!c_3!\cdots c_k!}\dfrac{c_2}{n}+\cdots+\dfrac{n!}{c_1!c_2!c_3!\cdots c_k!}\dfrac{c_k}{n}\\&=\binom{n}{c_1 \ c_2\ c_3 \cdots \ c_k} \dfrac{c_1+c_2+\cdots+c_k}{n}\\&=\binom{n}{c_1 \ c_2\ c_3 \cdots \ c_k}\end{aligned} \]

多项式定理

\[(x_1+x_2+\cdots + x_k)^n=\sum_{c_1+c_2+\cdots+c_k=n,c_i\geq 0,c_i\in\mathbb{Z}}\binom{n}{c_1 \ c_2\ c_3 \cdots \ c_k} x_1^{c_1}x_2^{c_2}\cdots x_k^{c_k} \]

我们把 \((x_1+x_2+\cdots+x_k)^n\) 展开。对于 \(x_1^{c_1}x_2^{c_2}\cdots x_k^{c_k}\) 这一项，会在展开的式子中出现 \(\binom{n}{c_1 \ c_2 \ c_3\ \cdots \ c_k}\) 次。

对展开后的式子合并同类项，最终不同的项会有 \(\binom{n+k-1}{k-1}\) 个（考虑转化为不定方程整数解问题）。

8. 卡特兰数

对于一个长度为 \(2n\) 的 01 序列 \(A\)，含有 \(n\) 个 \(0\) 和 \(n\) 个 \(1\)，满足对于任意的 \(i \in [1,2n]\)，\(A[1\sim i]\) 中 \(1\) 的个数不超过 \(0\) 的个数。

这样的 \(A\) 的个数，我们记为 \(Cat_n\)，也就是卡特兰数的第 \(n\) 项。

求法 1

欲求出 \(Cat_n\) 的值，不妨利用容斥，用总方案数 \(\binom{2n}{n}\) 减去不合法的方案数。

对于一个不合法的数列 \(B\)，存在一个位置 \(2p+1\)，满足 \(B[1\sim i]\) 中 \(0,1\) 分别出现了 \(p,p+1\) 次。那么 \(B[2p+2\sim 2n]\) 中 \(0,1\) 分别出现了 \(n-p,n-p-1\) 次。

反转 \(B[2p+2\sim 2n]\) 的每个元素，\(0\) 变 \(1\)，\(1\) 变 \(0\)。那么我们得到了一个含有 \(n+1\) 个 \(1\)，\(n-1\) 个 \(0\) 的数列。

对于一个含有 \(n+1\) 个 \(1\)，\(n-1\) 个 \(0\) 的数列 \(C\)，也存在一个这样的 \(2p+1\)。反转 \(C[2p+2\sim 2n]\)，又得到了一个含有 \(n\) 个 \(0\) 和 \(n\) 个 \(1\) 的数列。

每一个 \(B\) 都能得到一个唯一的 \(C\)，反过来亦然。那么不合法的方案数就是 \(C\) 的个数，即 \(\binom{2n}{n+1}\)。

于是我们得到：

\[Cat_i=\binom{2n}{n}-\binom{2n}{n+1}=\dfrac{\binom{2n}{n}}{n+1} \]

求法 2

\(Cat_n\) 也可以表述为：在平面直角坐标系中，每次允许向 \(x\) 或 \(y\) 的正方向移动一格，从 \((0,0)\) 不超过 \(y=x\) 这条直线走到 \((n,n)\) 的方案数。

那么如果我们移动过程中触碰到了 \(y=x+1\) 这条直线，必定不合法。

考虑类似于 "反射" 的转化：如果触碰到了 \(y=x+1\)，那么移动 \(x\) 变为移动 \(y\)，移动 \(y\) 变为移动 \(x\)。最终我们会到达 \((n,n)\) 关于 \(y=x+1\) 的对称点 \((n-1,n+1)\)。

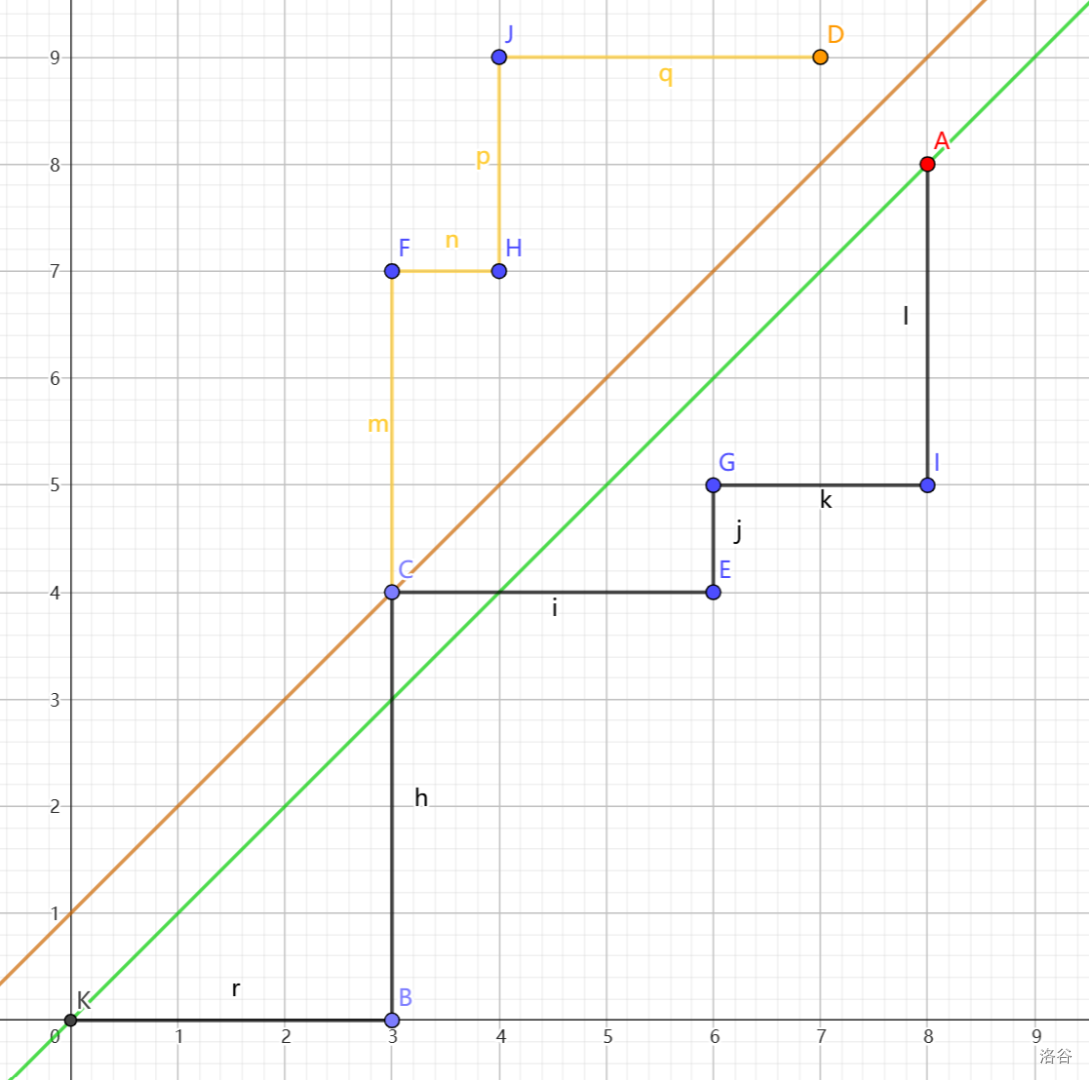
图中黑色折线为原路径，黄色折线为 “反射” 得到的直线。

那么不合法的走法有 \(\binom{2n}{n+1}\) 种，也可以得到与求法 1 相同的表达式。

卡特兰数的应用

1. 长度为 \(2n\) 的括号序列个数为 \(Cat_n\)；
2. \(n\) 个元素按顺序进栈，出栈序列的个数为 \(Cat_n\)；
3. \(n\) 个节点能够构造出 $Cat_n $ 种不同的二叉树。
4. ...

卡特兰数还有递推形式：

\[f_i=\sum_{j=1}^i (f_{i-1}\times f_{i-j}) \]

卡特兰数的前 \(10\) 项 （从 \(0\) 开始）：

\[1,1,2,5,14,42,132,429,1430,4862,... \]

9. 卢卡斯定理（Lucas）

Theorem

\[\binom{n}{m} \equiv \binom{\lfloor \frac{n}{p} \rfloor}{\lfloor \frac{m}{p} \rfloor} \times \binom{n \bmod p}{m \bmod p} \pmod{p} \]

其中 \(p\) 为质数。

也就是把 \(n,m\) 表示为 \(p\) 进制数，对于每一位都分别求解再相乘。

适用于 \(n,m\) 都很大，但 \(p\) 较小时的情况。

Proof

引理：若 \(p\) 为质数，则 \((1+x)^p \equiv 1+x^p \pmod{p}\)。

将 \((1+x)^p\) 利用二项式定理展开，得 \((1+x)^p = \sum\limits_{i=0}^p \binom{p}{i}x^i\)。

利用吸收恒等式变形： \(\sum\limits_{i=0}^p \binom{p}{i}x^i = 1+\sum\limits_{i=1}^p \dfrac{p}{i}\binom{p-1}{i-1}x^i\)。

对于 \(\forall i \in [1,p)\)，\(\dfrac{p}{i}\binom{p-1}{i-1} \mid p\)，则有 \((1+x)^p \equiv 1+x^p \pmod{p}\)。命题得证。

设 \(n=sp+q,m=tp+r\)。问题转化为证明 \(\binom{n}{m} \equiv \binom{s}{t} \times \binom{q}{r} \pmod{p}\)。

\(\binom{n}{m}\) 即为 \((1+x)^n\) 中 \(x^m\) 项的系数。

\[\begin{aligned}(1+x)^n &\equiv (1+x)^{sp+q} &\pmod{p}\\&\equiv (1+x)^{sp} \times (1+x)^q &\pmod{p}\\&\equiv [(1+x)^p]^s \times (1+x)^q &\pmod{p}\\&\equiv (1+x^p)^s \times (1+x)^q &\pmod{p}\\&\equiv (\sum\limits_{i=0}^s\binom{s}{i}x^{ip})(\sum\limits_{i=0}^q\binom{q}{i}x^i) &\pmod{p}\end{aligned} \]

由于 \(x^m = x^{tp+r} = x^{tp}\times x^r\)，\(x ^ m\) 的系数也可表示为 \(\binom{s}{t} \times \binom{q}{r}\)。

则有 \(\binom{n}{m} \equiv \binom{\lfloor \frac{n}{p} \rfloor}{\lfloor \frac{m}{p} \rfloor} \times \binom{n \bmod p}{m \bmod p} \pmod{p}\)，命题得证。

利用 Lucas 定理，可以在 \(O(p)\) 处理阶乘数组与阶乘逆元数组后， \(O(\log_p n)\) 求出 \(\binom{n}{m} \bmod p\) 的值。

void Init(){
    fac[0]=caf[0]=1;
    for(int i=1;i<p;i++) fac[i]=fac[i-1]*i%p;
    caf[p-1]=QuickPow(fac[p-1],p-2);
    for(int i=p-2;i;i--) caf[i]=caf[i+1]*(i+1)%p;
}

ll C(int x,int y){
    if(x<y) return 0;
    return fac[x]*caf[y]%p*caf[x-y]%p;
}

ll Lucas(int x,int y){
    if(x<p&&y<p) return C(x,y);
    else return Lucas(x/p,y/p)*C(x%p,y%p)%p;  
}

10. 阶乘的素数幂次

设 \(p \in \mathbb{Prime}\)，则有：

\[v_p(n!)=\sum_{i>0} \lfloor\dfrac{n}{p^i} \rfloor \]

其中 \(v_p(x)\) 表示 \(x\) 中包含 \(p\) 的次数。

将 \(1\sim n\) 分开，\(v_p(n!)=\sum_{i=1}^n v_p(i)\)。

\(1\sim n\) 中至少包含一个 \(p\) 的数字有 \(\lfloor \dfrac{n}{p} \rfloor\)，统计进答案中。\(1 \sim n\) 中至少包含 \(2\) 个 \(p\) 的数字有 \(\lfloor \dfrac{n}{p^2} \rfloor\) 个，但由于已经有一个 \(p\) 被统计过一遍，所以只需要再统计第 \(2\) 个质因子，答案加上 \(\lfloor\dfrac{n}{p^2}\rfloor\)，系数为 \(1\)。

我们从另一个角度来计算。用 \(p\) 进制表示 \(n\)，\(n=\sum a_ip^i(0\leq a_i<p)\)。

\[v_p(n!)=\sum_{j\geq1} \lfloor\dfrac{\sum_{i\geq 0}a_ip^i}{p^j}\rfloor = \sum_{i \geq 0}\sum_{j\geq 1} a_i \lfloor p^{i-j}\rfloor =\sum_{i\geq 0}a_i\sum_{j=0}^{i-1}p^{j}=\sum_{i\geq 0}a_i \dfrac{p^i-1}{p-1}=\dfrac{n-s_p(n)}{p-1} \]

其中 \(s_p(n)\) 表示 \(n\) 在 \(p\) 进制下各数位的数字之和。

11. Kummer 定理

\[v_p\left( \binom{n}{m} \right)=v_p\left(\dfrac{n!}{(n-m)!m!}\right)=v_p(n!)-v_p((n-m)!)-v_p(m!)=\dfrac{s_p(m)+s_p(n-m)-s_p(n)}{p-1} \]

在 \(p\) 进制下 \(n-m\) 与 \(m\) 相加，结果为 \(n\)。

设进位次数为 \(c\)。每进位一次，数位之和就会减少 \(p-1\)，那么有

\[s_p(n-m)+s_p(m)-c(p-1)=s_p(n) \Rightarrow c=\dfrac{s_p(m)+s_p(n-m)-s_p(n)}{p-1} \]

于是得到 \(\binom{n}{m}\) 中 \(p\) 的次数，就是 \(n-m\) 与 \(m\) 在 \(p\) 进制下相加进位次数。

同理可得， \(\binom{n}{m}\) 中 \(p\) 的次数就是 $n $ 与 \(m\) 在 \(p\) 进制下相减的借位次数。

若 \(\binom{n}{m}\) 在模 \(p\) 意义下为 \(0\)，那么 \(n,m\) 在 \(p\) 进制下相减时至少产生了一次借位。

换句话说，如果在 \(p\) 进制下存在一位，使得 \(n\) 在这一位的值小于 \(m\) 在这一位的值，那么 \(\binom{n}{m} \bmod p\) 一定为 \(0\)。

由此可以快速判断 \(\binom{n}{m}\) 的奇偶性：\(\binom{n}{m}\) 为奇数当且仅当 \(n \operatorname{and} m = m\)。

12. 扩展卢卡斯定理（Exlucas）

计算 \(\dbinom n m \bmod p\)，\(p\) 不要求是质数。

首先将 \(p\) 分解质因数得 \(p=\prod q_i^{k_i}\)。若 \(k_i=1\)，那么可以分别求出 \(\binom n m \bmod q_i\) 的值，然后 CRT 合并。

重点考虑 \(k_i>1\) 的情况，求 \(\binom n m \bmod q^k\)。

首先将阶乘中的 \(q\) 因子全部除掉：

\[\binom n m=\frac{n!}{m!(n-m)!}=\frac{\frac{n!}{q^{v_q(n!)}}}{\frac{m!}{q^{v_q(m!)}}\frac{(n-m)!}{q^{v_q((n-m)!)}}}\times q^{v_q(n!)-v_q(m!)-v_q((n-m)!)} \]

这样就有逆元了。

由 Kummer 定理，后半部分 \(q\) 的指数是 \(O(\log n)\) 的，可以直接算。

接下来考虑求 \(\dfrac {n!}{q^{v_q(n!)}}\bmod q^k\)。将 \(1\sim n\) 中的数字分为两类，分别计算：

• \(i\) 是 \(q\) 的倍数。设 \(d=\lfloor\frac n q \rfloor\)，这样的 \(i\) 有 \(q,2q,3q,\cdots,dq\)，贡献为 \(\dfrac{d!}{q^{v_q(d!)}}\)，是子问题，递归求解；
• \(i\) 不是 \(q\) 的倍数。在模 \(q^k\) 意义下有循环节，设 \(c=\lfloor\frac{n}{q^k} \rfloor,r=n\bmod q^k\)，则这部分的贡献为 \((q^k!)_q^{c}\times (r!)_q\)。前半部分的 \((q^k!)_q\) 可以扩展 Wilson \(O(1)\) 计算，后面的 \((r!)_q\) 可以预处理。

综上，

\[\dfrac {n!}{q^{v_q(n!)}}\equiv\dfrac{d!}{q^{v_q(d!)}}\times(q^k!)_q^{c}\times (r!)_q \pmod{q^k} \]

递归边界为 \(n<q\)，可以直接返回 \((n!)_q\)。

预处理复杂度 \(O(p)\)，查询复杂度 \(O(\omega(p)\log n)\)。

ll prd[N];
bool type;

void Exgcd(ll a,ll b,ll &x,ll &y){
	if(!b) return x=1,y=0,void();
	Exgcd(b,a%b,y,x); y-=a/b*x;
}

ll Inv(ll x,ll d){
	ll y,z;
	Exgcd(x,d,y,z);
	return (y%d+d)%d;
}

ll Calc(ll n,ll q,ll qk){
	if(n<q) return prd[n];
	ll d=n/q,c=n/qk,r=n%qk;
	return Calc(d,q,qk)*((type==1&&(c&1))?(qk-1):1)%qk*prd[r]%qk;
}

ll Num(ll n,ll q){
	ll res=0;
	while(n){
		res+=n/q;
		n/=q;
	}
	return res;
}

ll Solve(ll n,ll m,ll q,ll qk){
	prd[0]=1;
	for(int i=1;i<=qk;i++) prd[i]=prd[i-1]*(i%q==0?1:i)%qk;
	type=(q!=2)||(qk<=4);
	ll ans=Calc(n,q,qk)*Inv(Calc(m,q,qk),qk)%qk*Inv(Calc(n-m,q,qk),qk)%qk;
	int pw=Num(n,q)-Num(m,q)-Num(n-m,q);
	while(pw--) (ans*=q)%=qk;
	return ans;
}

ll ExLucas(ll n,ll m,ll p){
	ll ans=0,P=p;
	for(int q=2;q*q<=p;q++){
		if(p%q) continue;
		ll qk=1;
		while(p%q==0) p/=q,qk*=q;
		(ans+=Solve(n,m,q,qk)*(P/qk)%P*Inv(P/qk,qk)%P)%=P;
	}
	if(p>1) (ans+=Solve(n,m,p,p)*(P/p)%P*Inv(P/p,p)%P)%=P;
	return ans;
}

signed main(){
	ll n,m,p;
	read(n),read(m),read(p);
	printf("%lld\n",ExLucas(n,m,p));
	return 0;
}