概率论与数理统计

目录

• 基础
• 各种分布
  • 0-1分布
  • 二项分布,X ~ B(n,p)
  • Poisson分布，X ~ P($\lambda$)
  • 几何分布，X ～ GE(p)
  • 超几何分布
  • 正态分布，X ～ N($\mu$,$\sigma^2$)
  • 二维正态分布
  • 指数分布，X ~ $E(\lambda)$
  • 均匀分布，X ~ U(a,b)
  • 已知X为连续型随机变量，Y = g(x),且已知X的概率密度为$f_X(x)$,求Y的概率密度
    • 分布函数法
    • 公式法
• 随机变量的数字特征
  • 期望，加权平均和
  • 方差，随机变量可能取值与其均值的偏离程度
  • 协方差,随机变量之间的相关关系
  • 相关系数，刻画变量之间的线性关系

基础

频率 = $\frac{n次实验中事件的发生次数}{n}$
当n趋向于无穷大的时候，频率 = 概率

---

条件概率，指在事件A已经发生的概率下，事件B发生的概率，记为$P(B|A) = \frac{P(AB)}{P(A)}$，也就是A交B在A里面占的比重

事件的独立性，如果P(B|A) = P(B),说明事件A对事件B的发生没有影响，也就是P(AB) = P(A)P(B),称A、B相互独立
这个独立性就是，说，事件A，B的交集是空

---

贝叶斯公式

---

分布函数：称$F(x) = P(X \leq x)$，为变量X的分布函数
性质：
1.$F(-\inf) = 0$,$F(\inf) = 1$
2.$F(x)$单调不减
3.$F(x)$是右连续的，即$F(x) = F(x + 0)$
如果$F(x)$满足上述条件，那么他必然是某个随机变量的分布函数
概率密度函数 = 分布函数的导函数，注意概率密度函数的值没有实际的意义
概率密度函数的积分区间 = 某些事件发生的概率
同时$P(a < X < b) = P(a \leq X \leq b) = P(a < X \leq B) = P(a \leq X < b)$

各种分布

0-1分布

E(x) = p
D(x) = p(1 - p)

X	0	1
P	1 - p	p

二项分布,X ~ B(n,p)

E(x) = np
D(x) = np(1 - p)
n次相互独立的0-1分布实验 （也叫n重伯努利实验）
X ~ B(12,$\frac{1}{3}$)
P(X = 2 ) = $C_{12}^{2}(\frac{1}{3})^2(1 - \frac{1}{3})^{12 - 2}$

---

Poisson定理，当n很大，p很小时，令$\lambda = np$
$C_{k}^{n}p^k(1 - p)^{n - k} \approx \frac{\lambda^k}{k!}e^{-\lambda}$

Poisson分布，X ~ P($\lambda$)

E(x) = $\lambda$
D(x) = $\lambda$
P(X = k) = $C_{k}^{n}p^k(1 - p)^{n - k} \approx \frac{\lambda^k}{k!}e^{-\lambda}$

几何分布，X ～ GE(p)

就是射击命中率为p，射击k次才成功的概率
P(X = k) = $(1 - p)^{k - 1}p$

超几何分布

E(x) = $\frac{nM}{N}$
D(x) = $\frac{nM(N - M)(N - n)}{N^2(N - 1)}$

正态分布，X ～ N($\mu$,$\sigma^2$)

E(x) = $\mu$
一般将正态分布化为标准正态分布，X ~ N(0,1)进行分析

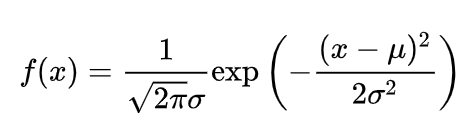
最大值 = $\frac{1}{\sigma \sqrt{2 \pi}}$,$\sigma$越小，曲线越陡峭

---

假设X ~ N(0,1)，有$\Psi(x) + \Psi(-x) = 1$
概率密度函数：$\psi(x) = \frac{1}{\sqrt{2 \pi}}e^{-\frac{x^2}{2}}$
分布函数： $\Psi(x) = \int_{-\inf}^{x} \frac{1}{\sqrt{2 \pi}}e^{-\frac{t^2}{2}} dt$

标准化：有X ～ N($\mu$,$\sigma^2$)
则分布函数为$F(x) = \Psi(\frac{x - \mu}{\sigma})$
注意3$\sigma$原则

二维正态分布

指数分布，X ~ $E(\lambda)$

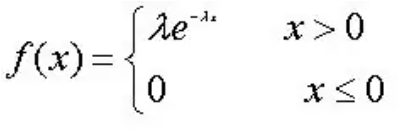
指数分布的无记忆性：
$\forall s,t > 0$
P(X > s + t | X > s) = P(X > t)

均匀分布，X ~ U(a,b)

E(x) = $\frac{a + b}{2}$
D(x) = $\frac{(b - a)^2}{12}$

已知X为连续型随机变量，Y = g(x),且已知X的概率密度为$f_X(x)$,求Y的概率密度

分布函数法

$F_X(x) = e^{-x},x > 0$
求随机变量，Y = $e^X$的概率密度
$F_Y(y) = P(Y <= y) = P(e^X <= y)$ , $Y \geq 1$ 时

$F_Y(y) = P(e^X \leq Y) = P(X \leq ln(y)) = \int_0^{ln(y)} e^{-x} dx$

从而Y的概率密度函数为
$F_Y(y) = \frac{dF_Y(y)}{dy} = \frac{1}{y^2},y > 1$

公式法

由于y = $e^x$严格单调可微，其反函数为x = h(y) = ln(y),y > 0,因此Y的概率密度函数为
$f_Y(y) = F_X(h(y))|h'(y)| = \frac{1}{y^2},y > 1$

随机变量的数字特征

期望，加权平均和

期望，E(x^k),这个一定要按积分定义去算，E(x + y) = E(x) + E(y)
y = g(x)的时候，求E(y),相对于把E(x)的积分定义中的x替换为g(x)，其他不变

---

当X，Y相互独立的时候，E(XY) = E(X)E(Y)

方差，随机变量可能取值与其均值的偏离程度

D(X) = $E(X - E(X))^2$ = $E(X^2)$ - $E(X)^2$
D(CX) = $C^2D(X)$
D(X + C) = $D(X)$
如果X、Y相互独立，$D(c_1X + c_2Y) = c_1^2D(X) + c_2^2D(Y)$

协方差,随机变量之间的相关关系

cov(X,Y) = E((X - E(X)) * (Y - E(Y))) = E(XY) - E(X) * E(Y)
cov(X,X) = D(X)
cov(aX + b,cY + d) = accov(X,Y)
cov(X + Y,Z) = cov(X,Z) + cov(Y,Z)
D(X + Y) = D(X) + D(Y) + 2cov(X,Y)
D(X - Y) = D(X) + D(Y) - 2cov(X,Y)

相关系数，刻画变量之间的线性关系

$\rho_{XY} = \frac{cov(X,Y)}{\sqrt{D(X)} \sqrt{D(Y)}}$
若随机变量X,Y相互独立，且方差均大于0，则$\rho_{XY} = 0$

---

$|\rho_{XY}| = 1$的充要条件差是，存在常数$a \neq 0$,b,使得P(Y = aX + b) = 1

---

若A、B是随机事件，
$\rho = \frac{P(AB) - P(A)P(B) }{\sqrt{P(A)P(A补)} \sqrt{P(B)P(B补)}}$

---

注意相关关系描述的是线性关系的强弱，而独立关系是更强的关系
可能不相关，但不独立、