IEEE浮点数

说明

对于IEEE浮点标准的详细解读

前置知识

在线浮点转换器


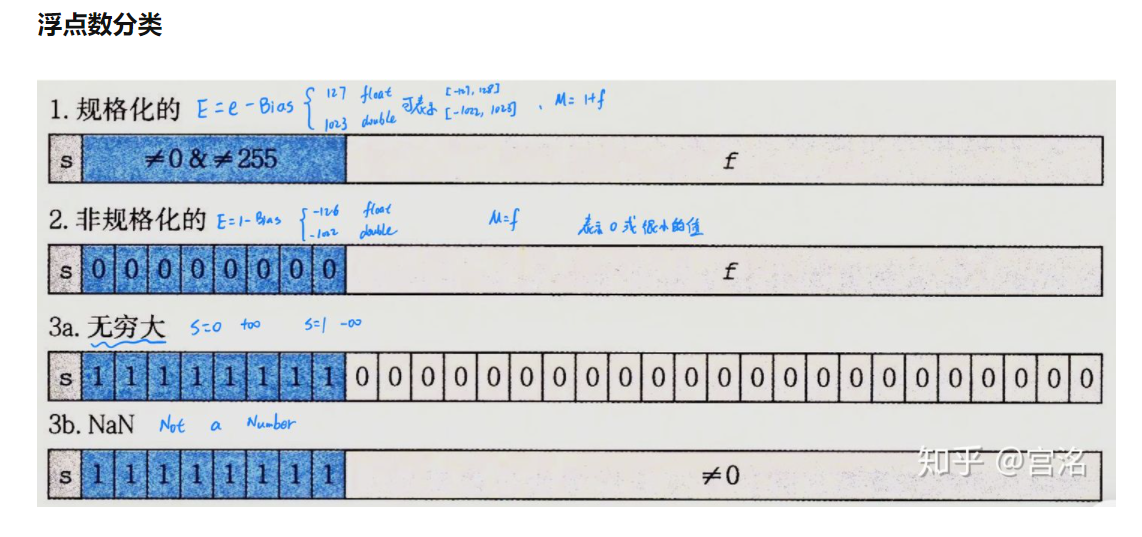
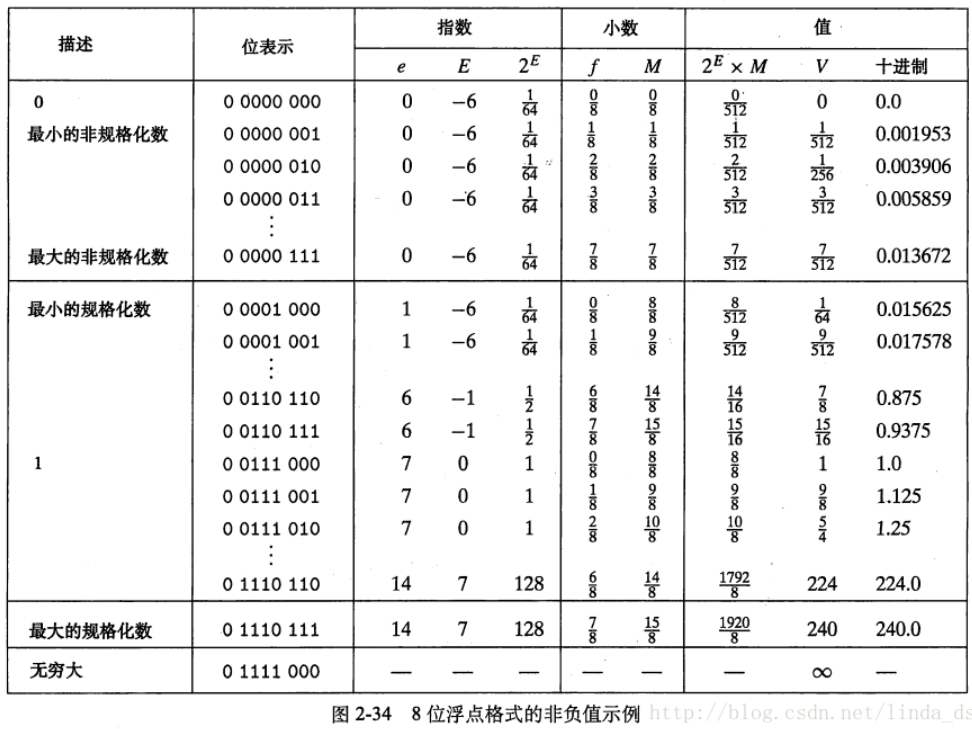
值得注意的是阶码的值是E = e - Bias，其中e是无符号整数，Bias是一个等于\(2^{k-1} - 1\)的值,单精度是127，双精度是1023
由此产生指数的取值范围，对于单精度是[-126,+127],双精度是[-1022,+1023]
这种比较奇怪的办法提供了规格化数值到非规格化数值的平滑转变

舍入规则

任何有效数上的运算结果，通常都存放在较长的寄存器中，当结果被放回浮点格式时，必须将多出来的比特丢弃。 有多种方法可以用来运行舍入作业，实际上IEEE标准列出4种不同的方法：

舍入到最接近 (默认的舍入方式)

这种舍入方式可以尽可能消除统计上的偏差
其实就是舍入到偶数，也就是保证末尾为0

朝\(+\infty\)方向舍入

会将结果朝正无限大的方向舍入

朝\(+\infty\)方向舍入

会将结果朝负无限大的方向舍入

朝0方向舍入

会将结果朝0的方向舍入

浮点乘法

步骤

1.符号位异或
2.指数相加
3.尾数相乘三部分。

浮点加法

1.对阶

原则是小阶对大阶
这样在对阶时丢失的是尾数的低位，造成的误差很小

2.尾数相加

减法做补码加法即可

3.结果规格化

这里有左归和右规两种情况
左归下溢出时，结果为0
右归上溢出时，结果为\(\inf\)

4.舍入

1.截断法
2.末位恒置1
3.0舍1入
这种方法误差小，但是遇到01.111...111时会使尾数溢出，特判即可

浮点异常

IEEE 754 还提出 5 种类型的浮点异常，即上溢、下溢、除以零、无效运算和不精确。