深入理解计算机基础第二章-家庭作业答案
第三版和第二版的题目略有差异
本篇文章以第二版为标准
2.57
写个模板,比较方便
printf("%.2x",0xff); 输出ff
printf("%.2X",0xff) ;输出FF
template<typename T>
void show_bytes(T const& val)
{
unsigned char*p = (unsigned char*)(&val);
for (unsigned i = 0;i < sizeof(val);i++)
printf("%.2x",p[i]);
}
2.58
判断大小端的两种办法:
1.读取宏定义
#include <sys/types.h>
#include <sys/param.h>
2.利用union或者指针读取int的前几位
这里有个问题就是,c/c++标准没有规定int,char之类的长度,在任意位字长机器上一些做法可能失效
直接采用stdint.h中的定长整形 __int32 和 uint8_t(unsigned char)就行了
bool is_little_endian()
{
__int32 val = 0x12345678;
uint8_t *p = (uint8_t*)(&val);
return *p == 0x78;
}
2.59
__int32 comb(__int32 a,__int32 b)
{
return (a & 0xFF) | (b & (-1 ^ 0xFF));
return (a & 0xFF) | (b ^ (b & 0xFF));
}
因为 -1的类型是int,那么-1 ^ 0xFF的类型也是int,不管b的类型是啥,(-1 ^ 0xFF)都会正确扩展到 0xFFFFFFFF....FFF00,所以两个写法都可以
2.60
...网上一些利用unsigned char* 直接对x的某个字节赋值的代码是错的,因为大小端的问题...
c/c++标准规定了char、unsigned char、signed char的大小都是8bit,值得一提的是char的类型不固定,可能是signed char,也可能是unsigned char
unsigned replace_byte(unsigned x,unsigned char b,int i)
{
return x ^ (unsigned(b) << i * 8) ^ (x & (0xFFU << i * 8));
}
2.61
没想到,百度了一下...关键就是 !(0) = 1,CD位运算凑一下全0全1就行了,网上有些答案不太对劲,不要轻信
A.!(~x)
B.!x
C.!(~(x | 0x00FFFFFF))
D.!(x & (0xFF))
2.62
emm,比较憨憨的题?利用算数右移,在负数情况下高位补1的性质即可,最简单的就是取 -1 ,-1算数右移一位还是-1
bool int_shifts_are_logical()
{
int x = -1;
return !(x == (x >> 1));
}
2.63
老样子,处理一下算数右移的时候,负数高维补0的情况即可,异或实现不借位减法
int sra(int x,int k)
{
int xsrl = (unsigned)x >> k;
if (x >= 0 or k == 0)
return xsrl;
else
{
int val = -1 ^ ((1 << sizeof(int) * 8 - k) - 1);
return val | xsrl;
}
}
unsigned srl(int x,int k)
{
unsigned xsra = (int)x >> k;
if (x >= 0 or k == 0)
return xsra;
else
{
int val = -1 ^ ((1 << sizeof(int) * 8 - k) - 1);
return val ^ xsra;
}
}
2.64
翻译 : 若x的任何一个偶数bit位为1,返回1,其他返回0
也不给个样例啥的,假设从下标从0开始
int any_even_one(unsigned x)
{
return bool(x & 0x55555555);
}
2.65
这个题比较hard,(可以写汇编直接从状态寄存器读取出来,大雾
我想的是,要用异或把所有位压到一起,然后每次利用 &0xFF 这样提取一部分,但是这样会多操作很多次
正确的姿势是折半压缩,每次分两半,把高位直接异或进低位....学到了.jpg
int even_ones(unsigned x)
{
x ^= x >> 16;
x ^= x >> 8;
x ^= x >> 4;
x ^= x >> 2;
x ^= x >> 1;
return !(x & 0x1);
}
2.66
就是求个higbit,如higbit(6) = 4,higbit(8) = 8
orz_还是要做题...新姿势get.jpg
key point : 把 x 变成 [0000...11111]的形式
然后 !(x & x >> 1)就得到了答案
怎么变成[0000...1111111]的形式?采用倍增的思想
比如32(000100000b)
做 x |= x >> 1,变成000110000b
做 x |= x >> 2,变成000111100b
做 x |= x >> 4,变成000111111b
每个1都会倍增的向低位扩展,做5次就行了,很巧妙
int leftmost_one(unsigned x)
{
x |= x >> 1;
x |= x >> 2;
x |= x >> 4;
x |= x >> 8;
x |= x >> 16;
return x ^ (x >> 1);
}
2.67
A.1 << inf这样是未定义行为,有的编译器会取模,有的编译器会截断
强调一下,未定义行为摧毁一切定义,网上很多代码都是采用了 1 << k 溢出来判断是否为int32
这是不对的...signed的溢出是未定义行为...
注意UB的细节...否则你的代码会被UB摧毁...比如开O2的时候,很多UB会直接暴露...导致各种诡异的错误...
未定义行为摧毁一切定义!!!
书上的思路就是错的,正确的姿势是利用1 << k会在某个时候从正数变成负数,这样判断并不慢,并且没有溢出
#include <bits/stdc++.h>
using namespace std;
using ll = long long int;
template<typename T>
int count()
{
int ret = 0;
T now = 1;
while (now > 0)
now <<= 16,
ret += 16;
return ret;
}
int main()
{
cout << count<int>() << " " << count<ll>() << " " << count<short>();
return 0;
}
2.68
注意一下n >= w的情况
int lower_bits(int x,int n)
{
if (n >= 32)
return 0xFFFFFFFF;
else
return x | ((1 << n) - 1);
}
2.69
简单题,注意处理n比较大的情况
unsigned rotate_right(unsigned x,int n)
{
n %= 32;
return (x >> n) | (x << (32 - n));
}
2.70
题目 : 给你一个补码表示的x,为能不能用n位补码表示x
...网上的一些代码是错的...
思路,n位补码会形成一个可以表示的范围,算出来判断一下x是不是在该区间内就行了
int fits_bits(int x,int n)
{
if (n >= sizeof(int) * 8)
return 1;
else
return -(1ll << n - 1) <= x and x <= (1 << n - 1) - 1;
}
还有一个很妙的做法,利用了补码右移根据正负补0、1的性质
int fits_bits(int x,int n)
{
int w = sizeof(int) * 8;
return x == (x << (w - n)) >> (w - n);
}
2.71
A.符号扩展...这&0xFF直接丢弃符号
B.
int xbyte(unsigned word,int bytename)
{
return int(word) << (24 - (bytename << 3)) >> 24;
}
2.72
int op unsigned 的时候,会把int提升成unsigned,再进行运算
所以maxbytes - sizeof(val)的类型是unsigned所以恒大于等于 0
改为maxbytes >= sizeof(val)即可
2.73
这个题本质上就是判断一下正溢出负溢出和不溢出
特别注意,c/c++中,无符号整形的加法乘法溢出是定义行为,但是,有符号的加法乘法溢出是未定义行为
网上利用 if (a > 0 and b > 0 and a + b < 0) 正溢出(); 的代码是错误的,只能在一些特定的机器上运行
正确的姿势是这样子的
1.正数 + 负数不会溢出
2.INT32_MAX和INT32_MIN不对称,要特判
3.注意UB(未定义行为)...很容易写出UB...INT32可以利用模板改成字长无关的,比较简单不写了
int is_add_overflow(int a,int b)
{
if (((a ^ b) & (1 << ((int(sizeof(int) * 8)) - 1))))
return 0;
if (a > 0 and b > 0 and a > INT32_MAX - b)
return 1;
else if (a < 0 and b < 0)
{
if (a == INT32_MIN or b == INT32_MIN)
return -1;
else if (a < INT32_MIN + (-b))
return -1;
else
return 0;
}
else
return 0;
}
int saturating_add(int a,int b)
{
int overflow = is_add_overflow(a,b);
if (overflow == 0)
return a + b;
else if (overflow < 0)
return INT32_MIN;
else
return INT32_MAX;
}
2.74
判断一下减法溢出,有了上一题的经验,简单很多
注意一下INT32_MIN和INT32_MAX之间的不对称性,转化为判断加法溢出就行了
int is_add_overflow(int a,int b)
{
if (((a ^ b) & (1 << ((int(sizeof(int) * 8)) - 1))))
return 0;
if (a > 0 and b > 0 and a > INT32_MAX - b)
return 1;
else if (a < 0 and b < 0)
{
if (a == INT32_MIN or b == INT32_MIN)
return -1;
else if (a < INT32_MIN + (-b))
return -1;
else
return 0;
}
else
return 0;
}
int is_sub_overflow(int a,int b)
{
if (b != INT32_MIN)
return is_add_overflow(a,-b);
else if (a >= 0)
return 1;
else
return 0;
}
int tsub_ovf(int a,int b)
{
return !!is_sub_overflow(a,b);
}
2.75
两层for暴力算就行了,直接实现unsigned_high_prod(unsigned,unsigned);
bool is_add_overflow(unsigned x,unsigned y)
{
return x > UINT32_MAX - y;
}
unsigned unsigned_high_prod(unsigned x,unsigned y)
{
int w = sizeof(unsigned) * 8;
unsigned ret = 0;
unsigned low = 0;
for (int i = 0;i < w;i++)
if (x & (1u << i))
{
for (int k = 0;k < w;k++)
if (y & (1u << k))
{
if (i + k >= w)
ret += 1u << i + k - w;
else
{
if (is_add_overflow(low,1u << i + k))
ret++;
low += 1u << i + k;
}
}
}
return ret;
}
2.76
A.(x << 2) + x
B.(x << 3) + x
C.(x << 5) - (x << 1)
D.(x << 3) - (x << 6)
2.77
一个比较笨但是有效的做法是:特判,非负整数x右移k位的时候,x >> k == x / 2^k,负数转化成正数判即可,INT32_MIN特判一下
int divide_power2(int a,int b)
{
if (b == 0)
return a;
else if (a >= 0)
return a >> b;
else if (a == INT32_MIN)
return divide_power2(INT32_MIN >> 1,b - 1);
else
return -divide_power2(-a,b);
}
网上很多做法是错的...麻了...建议写完动手测试一下...
这个做法比较奇妙
int divide_power2(int x,int k)
{
if ((x >> sizeof(int) * 8 - 1) == -1)
return (x + (1 << k) - 1) >> k;
else
return x >> k;
}
2.78
简单调用一下2.76中的divide_power2(5 * x,3)即可...网上一些代码做了比较复杂的分析...感觉学不到啥,没必要折磨自己看那玩意
2.79
可能翻译错了,这个表达式恒等于0
2.80
A.UINT32_MAX << n
B.((1 << n) - 1) << m
2.81
首先搞清楚,在C语言中,可以确定,对于任意整数值x,计算表达式-x和~x + 1得到的结果完全一样
又,INT32_MAX和INT32_MIN不对称,所以 -INT32_MIN 是个未定义行为...在大多数实现里面,-INT32_MIN = INT32_MIN...c/c++在数值这一块qs非常阴间...
下面仅在,g++上hack下列等式...不然因为UB的问题没法做...下面结果在大部分情况下是对的
A.否,x = 0,y = INT32_MIN
B.是,在大部分机器上补码溢出会做截断处理...此时加减乘具有结合律和交换律
C.否,x = 0,y = 0
D.是,大多数情况下是对的,类型转换和+-*在位级别等效...比较恶心的一点是,有符号加减溢出是UB...开O2就会return 0;x = -2147483648,y = 12
E.是
2.82
A.经典小学数学,显然Y = \(\frac{y}{2^k - 1}\)
B.a.\(\frac{1}{7}\)
B.b.\(\frac{3}{5}\)
B.c.\(\frac{1}{9}\)
下面的题要求对IEEE浮点标准比较熟
主要是这两张图...看懂了就没问题了
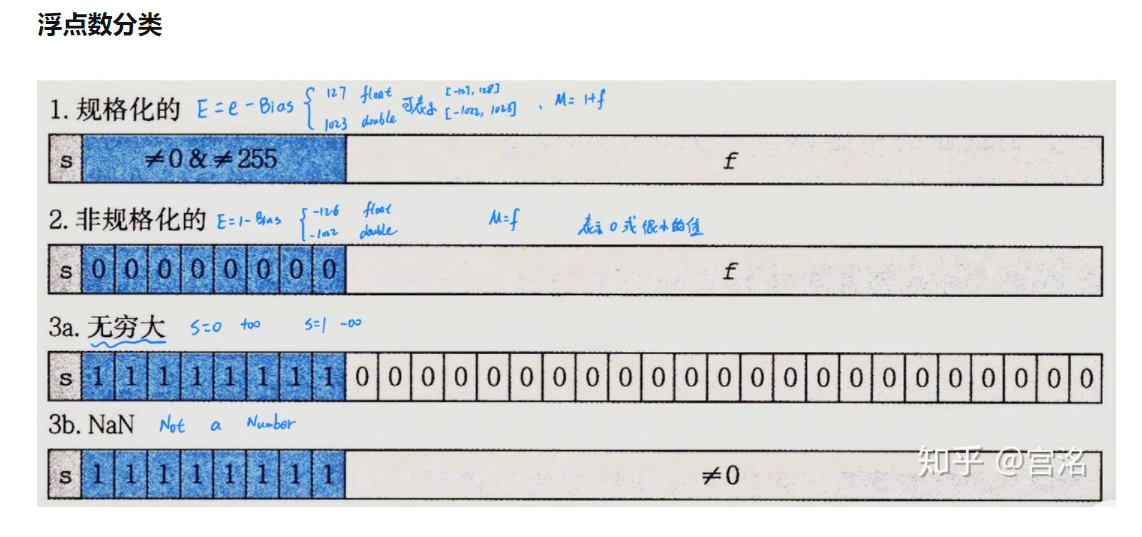
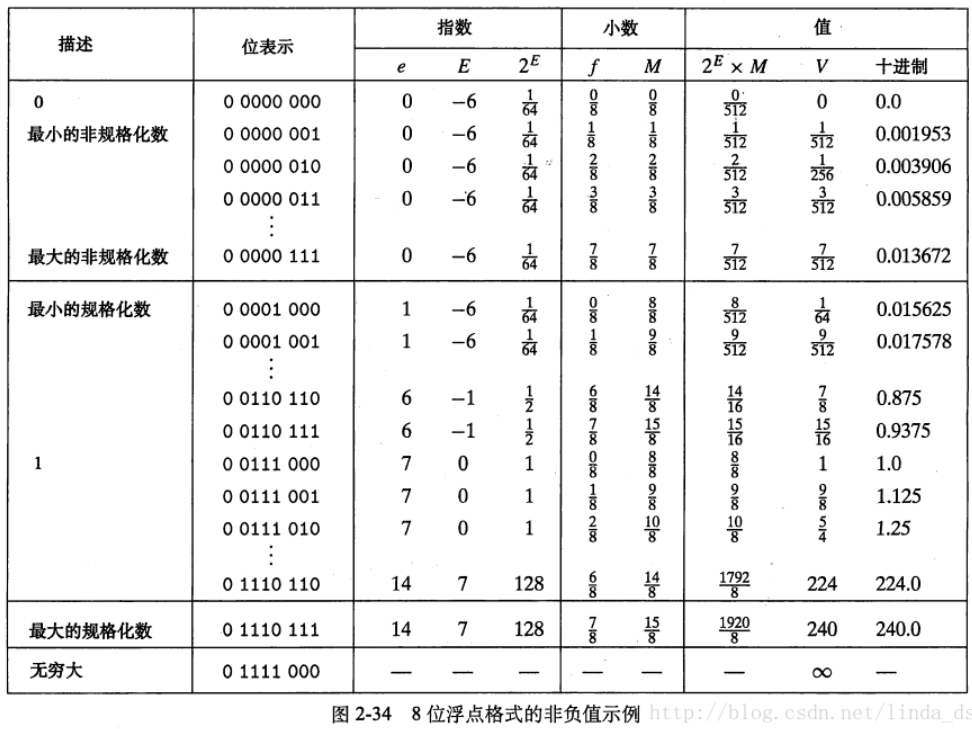
非规格化的尾数要 + 1
1.规格化到非规格化的转变是平滑的
2.除去符号位,把浮点看做无符号整数,那么可以按无符号整数排序,排序结果和按浮点排序一样
3.浮点运算有交换律,但没有结合律和分配率,这意味着编译器不会采取优化(哪怕是产生了很轻微的影响)
4.注意舍入的问题,以及-0.0的问题,以及把正整数变为浮点数的操作特性
本文来自博客园,作者:XDU18清欢,转载请注明原文链接:https://www.cnblogs.com/XDU-mzb/p/14797549.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号