浅谈线段树

对于提高组，线段树的重要性不言而喻

什么是线段树？

线段树是一颗二叉搜索树。之所以叫线段树，是因为线段树上每个节点维护的是序列的一段区间。

线段树可以广泛地解决各种区间问题。相比于朴素算法\(O(n^2)\)的复杂度，线段树可以在\(O(nlogn)\)的复杂度下解决问题。

线段树的结构

线段树利用了分治的思想

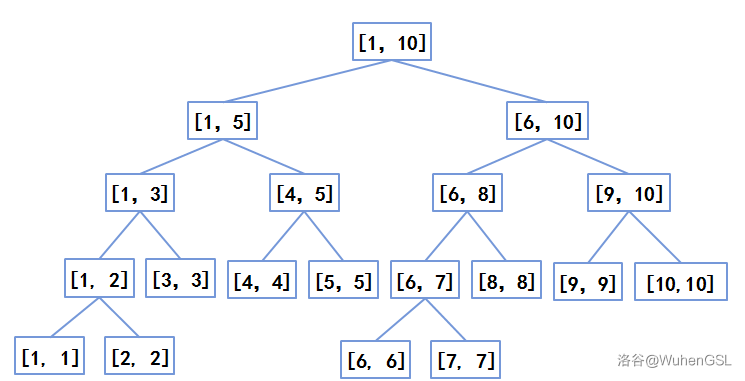
对于一颗线段树

每个节点维护一个闭区间\([l,r]\)的信息，根节点维护\([1,n]\)的信息

如果\(l=r\)就是叶子节点；如果\(l<r\)就是内部节点，它有两个节点\([l,\frac{l+r}{2}]\)和\([\frac{l+r}{2}+1,r]\)

同时，我们设 1 为根节点的下标

下标为\(x\)的左儿子的下标为\(2x\)，右儿子为\(2x+1\)

用\(sum[x]\)记录节点\(x\)代表的区间里所有数的和

对于叶子节点，因为\(l=r\)，所以\(sum[x]=a[l]\)

运用分治的思想，我们可以这样维护\(sum[x]\)：

struct tree{
	int l,r,sum;
}c[N<<2];
void update(int x)
{
	c[x].sum=c[x<<1].sum+c[x<<1|1].sum;
    //这里使用位运算速度更快，其中(x<<1)=(x*2)，(x<<1|1)=(x*2+1)
}

在了解线段树的结构之后，不难想出，可以用简单的递归得到一颗初始的线段树。需要注意的是，线段树的数组要开到\(4\times n\)的级别

void build(int l,int r,int x)//l,r为当前节点所代表的区间，x为当前节点编号
{
	c[x].l=l,c[x].r=r;//记录区间
	if(l==r){ //当前节点为叶节点
		c[x].sum=a[l]; //直接赋值
		return;
	}
	int mid=(l+r)>>1;
	build(l,mid,x<<1); //构造左子树
	build(mid+1,r,x<<1|1); //构造右子树
	update(x); //更新sum值
}

线段树基本操作

线段树的区间划分

想要理解线段树修改和查询操作，首先要理解线段树是如何划分区间的

划分\([3,8]\)

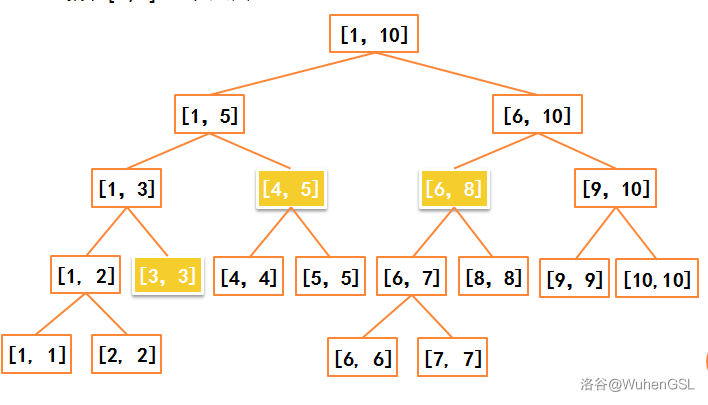
划分\([2,10]\)

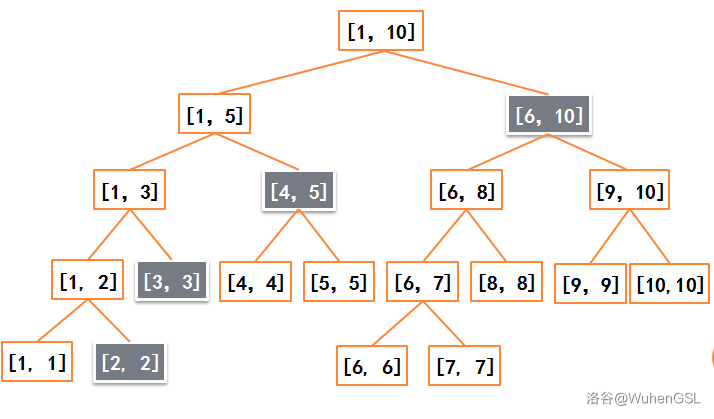
对于被划分的区间，我们用一些尽量大的区间去表示它

区间查询

以查询\([3,8]\)为例，我们只需要用的标黄的三个节点的信息

我们需要从上到下的找出所查询区间的几个组成部分

假设询问区间是 \([A,B]\)，现在所在的节点表示的区间为\([l,r]\)

计算 \(mid = \frac{l+r}{2}\)，左子节点的区间为 \([l,mid]\)，右子节点的区间为 \([mid+1,r]\).

如果 \(A \leq mid\)，即询问区间与左子节点有重合，需要递归到左子节点。

如果 \(B \geq mid + 1\)，即询问区间与右子节点有重合，需要递归到右子节点。

递归完之后，需要把两个孩子询问的结果加起来作为返回值。

代码实现：

int query(int l,int r,int x)//l,r为询问区间，x为当前节点编号
{
	if(c[x].l>=l&&c[x].r<=r) // 已经是询问区间的子区间
		return c[x].sum;
	int mid=(l+r)>>1,ans=0;
	if(l<=mid)ans+=query(l,r,x<<1); //查询左儿子
	if(r>mid)ans+=query(l,r,x<<1|1); //查询右儿子
	return ans;
        //此处ans已经是左右儿子之和，无需update
}

单点修改

由于修改是对单个元素进行修改。

比如修改第 \(i\) 个元素。

我们先从上往下找到 \([i,i]\) 所在的节点，然后修改它的 \(sum\)，然后一路向上更新每个祖先的 \(sum\) 即可。

void modify(int l,int r,int p,int z,int x) //l,r整个区间，p为需要修改的点，z为要改为的值 
{
	if(l==r){ //找到所求叶子节点 
		c[p].sum=z;
		return;
	}
	int mid=(l+r)>>1;
	if(p<=mid)modify(l,mid,p,z,x<<1); //p在左子树 
	else modify(mid+1,r,p,z,x<<1|1); //p在右子树 
	update(x); //sum值改变且没有向上累加，需要update 
}

区间修改和延迟修改技术(Lazytag)

如果把区间修改拆成 \(r - l + 1\) 个单点修改，效率非常的低。

我们希望区间修改和区间查询一样，先把区间分成线段树上的若干个区间。然后分别修改这几个区间。

如果要将区间\([3,8]\)都加上z

把黄色的节点都打上一个tag，表示这个子树里都加上\(z*(r-l+1)\)

此时如果要访问到\([5,5]\)，路上会碰到\([4,5]\)

而\([4,5]\)的tag是z，说明子树内的值发生了改变，但是还没有应用更改

此时将\([4,5]\)的标记下传给它的左右儿子，并清空自身的标记，完成标记下传

通过延迟修改操作，可以避免修改中多余的递归，复杂度降为\(O(logn)\)

void pushdown(int x)
{
	if(c[x].tag){ //如果有标记 
		c[x<<1].sum+=c[x].tag*(c[x<<1].r-c[x<<1].l+1); //更新左儿子sum 
		c[x<<1|1].sum+=c[x].tag*(c[x<<1|1].r-c[x<<1|1].l+1); //更新右儿子sum 
		c[x<<1].tag+=c[x].tag; //标记下传 
		c[x<<1|1].tag+=c[x].tag; //标记下传 
		c[x].tag=0; //清空当前标记 
	}
}
void change(int l,int r,int z,int x)
{
	if(c[x].l>=l&&c[x].r<=r){ //与区间查询类似 
		c[x].sum+=z*(c[x].r-c[x].l+1);
		c[x].tag+=z; //打lazytag 
		return;
	}	
	pushdown(x); //检查标记并下传 
	int mid=(c[x].l+c[x].r)>>1;
	if(l<=mid)change(l,r,z,x<<1);
	if(r>mid)change(l,r,z,x<<1|1);
	update(x);
} 

使用lazytag后，区间查询也需要检查标记

int query(int l,int r,int x)//l,r为询问区间，x为当前节点编号
{
	if(c[x].l>=l&&c[x].r<=r) // 已经是询问区间的子区间
		return c[x].sum;
        pushdown(x); //检查标记并下传
	int mid=(l+r)>>1,ans=0;
	if(l<=mid)ans+=query(l,r,x<<1); //查询左儿子
	if(r>mid)ans+=query(l,r,x<<1|1); //查询右儿子
	return ans;
        //此处ans已经是左右儿子之和，无需update
}

一些例题

P3372 线段树1

线段树裸题，考察区间修改和区间查询

P3373 线段树2

线段树维护多个tag

GSS系列

SPOJ的一系列线段树好题，是线段树的综合应用，这里放出我在洛谷上的题单