purfer序列
\(\bm{purfer}\)序列
- 概念:
转换\(1\):无根树\(\to\)\(purfer\)序列
现在,给一棵树,我们考虑如何把它变成\(prefur\)序列。
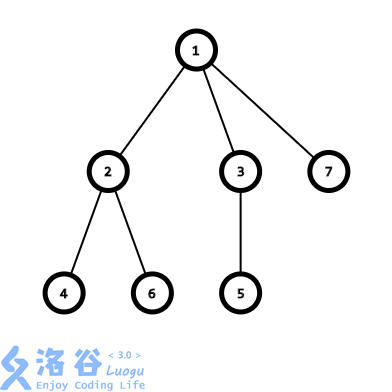
我们需要重复进行以下操作,直至树中只剩下两个点:
- 找到一个度数为\(1\),且编号最小的点(其中编号最小保证了后面将会提到的\(prufer\)序列的唯一对应性,同时也方便从\(prufer\)序列转化回无根树)
- 把这个点的父亲节点加入序列,然后把这个点从树中删除。
以上面的图为例,我们可以模拟这一过程如下:
- 找到\(4\)号节点,将其父结点加入序列,然后将其删去。此时序列:\(\{ 2 \}\)
- 找到\(5\)号节点,将其父结点加入序列,然后将其删去。此时序列:\(\{ 2,3 \}\)
- 找到\(3\)号节点,将其父结点加入序列,然后将其删去。此时序列:\(\{ 2,3,1 \}\)
- 找到\(6\)号节点,将其父结点加入序列,然后将其删去。此时序列:\(\{ 2,3,1,2 \}\)
- 找到\(2\)号节点,将其父结点加入序列,然后将其删去。此时序列:\(\{ 2,3,1,2,1 \}\)
所以,最后得到的\(prufer\)序列就是\(\{2,3,1,2,1\}\)。
转换\(2\):\(purfer\)序列\(\to\)无根树
还是以刚才那棵树为例,我们要考虑如何把它的\(prefur\)序列变回它本身。
我们需要重复进行以下操作,直至点集中只剩下两个点:(初始化所有点都在点集中)
- 取出\(prufer\)序列最前面的元素\(x\)
- 取出在点集中的、且当前不在\(prufer\)序列中的最小元素\(y\)
- 在\(x,y\)之间连接一条边
最后,我们在点集中剩下的两个点中连一条边。
显然这有\(n−1\)条边,且绝对不会形成环,因此它是一棵树,且就是原树。
以上面的序列为例,我们可以模拟这一过程如下:
- 取出\(2,4\)连边。此时\(prufer\)序列:\(\{3,1,2,1\}\),点集:\(\{1,2,3,5,6,7\}\)
- 取出\(3,5\)连边。此时\(prufer\)序列:\(\{1,2,1\}\),点集:\(\{1,2,3,6,7\}\)
- 取出\(1,3\)连边。此时\(prufer\)序列:\(\{2,1\}\),点集:\(\{1,2,6,7\}\)
- 取出\(2,6\)连边。此时\(prufer\)序列:\(\{1\}\),点集:\(\{1,2,7\}\)
- 取出\(1,2\)连边。此时\(prufer\)序列:\(\{\}\),点集:\(\{1,7\}\)
- 最后再在\(1,7\)间连边,就可以得到原树
\(prufer\)序列的性质及相关结论:
- \(prufer\)序列与无根树一一对应
- 度数为\(d_i\)的节点会在\(prufer\)序列中出现\(d_{i-1}\)次
- 一个\(n\)个节点的完全图的生成树个数为\(n^{n-2}\)
对于一个\(n\)个点的无根树,它的\(prufer\)序列长为\(n−2\),而每个位置有\(n\)种可能性,因此可能的\(prufer\)序列有\(n^{n-2}\)种
又由于\(prufer\)序列与无根树一一对应,因此生成树个数应与\(prufer\)序列种树相同,即\(n^{n-2}\) - 对于给定度数为\(d_{1\sim n}\)的一棵无根树共有\(\frac{(n-2)!}{\prod_{i=1}^n(d_i-1)!}\)种情况。
由上面的性质可以知道,度数为\(d_i\)的节点会在\(prufer\)序列中出现\(d_i-1\)次。
则就是要求出\(d_i-1\)个\(i(1\le i\le n)\)的全排列个数。
而上面那个式子就是可重全排列公式(即全排列个数除以重复元素内部的全排列个数)
\(purfer\)序列到底有啥实际意义也不是很清楚
- 例题
思路:利用性质:对于给定度数为\(d_{1\sim n}\)的一棵无根树共有\(\frac{(n-2)!}{\prod_{i=1}^n(d_i-1)!}\)种情况。
直接算阶乘的话肯定会炸··· 这里我们先记\(d_i=d_i-1\),再将柿子展开变形:
\[\frac{(n-2)!}{\prod_{i=1}^n d_i!}=\frac{(n-2)!}{d_1!*(n-2-d_1)!}*\frac{(n-2-d_1)!}{d_2!*(n-2-d_1-d_2)!}*···*\frac{(n-2-\sum d_i)!}{d_n!*(n-2-\sum d_i)!}\\
\quad\\
\frac{(n-2)!}{\prod_{i=1}^n d_i!}={n-2 \choose d_1}*{n-2-d_1 \choose d_2}*···*{n-2-(\sum d_i-d_n) \choose d_{n-1}}*{n-2-\sum d_i \choose d_n}
\]
因此求这\(n\)个组合数即可
PS:注意特判:只有一个节点时,度数不为\(0\)则不成立;\(\sum (d_i-1)\ !=n-2\)则不成立
Code:
#include <bits/stdc++.h>
using namespace std;
const int N=200+10;
typedef long long ll;
int n,d[N],c[N][N];
int main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>d[i];
int sum=0;
if(n==1){
if(d[1])cout<<"0"<<endl;
else cout<<"1"<<endl;
return 0;
}
for(int i=0;i<=n;i++){
c[i][0]=1;
for(int j=1;j<=i;j++){
c[i][j]=c[i-1][j]+c[i-1][j-1];
}
}
for(int i=1;i<=n;i++){
if(!d[i]) {
cout<<"0"<<endl;
return 0;
}
d[i]--;
sum+=d[i];
}
if(sum!=n-2) {
cout<<"0"<<endl;
return 0;
}
sum=0;
ll ans=1;
for(int i=1;i<=n;i++){
ans*=c[n-2-sum][d[i]];
sum+=d[i];
}
cout<<ans<<endl;
return 0;
}
思路:利用性质:一个\(n\)个节点的完全图的生成树个数为\(n^{n-2}\)
本题题意是求有根树,故答案为:\(n*n^{n-2}\)即\(n^{n-1}\)
Code:
#include <bits/stdc++.h>
using namespace std;
const int N=200+10,mod=1e9+9;
typedef long long ll;
ll n,t;
ll power(ll a,ll b){
ll ans=1;
for(;b;b>>=1){
if(b&1) ans=ans*a%mod;
a=a*a%mod;
}
return ans;
}
int main(){
cin>>t;
while(t--){
cin>>n;
ll ans=power(n,n-1);
cout<<ans<<endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号