浅谈算法——点分治

很多情况下，我们会遇到在树上进行操作的题目，比如求树上路径长度为\(k\)的路径条数

大力枚举？每次枚举两个点暴力算距离，时间复杂度\(O(n^3)\)，高级数结维护一下\(O(n^2\log n)\)，emmmm……，都TM高级数结维护都跑不了1w的数据，(╯°Д°)╯︵ ┻━┻

大力枚举肯定不行了，我们得换个想法，我们考虑一下每条路径，假如一个满足条件的路径经过\(x\)，那么这条路径要么以\(x\)为端点，要么两个端点在\(x\)的不同子树内

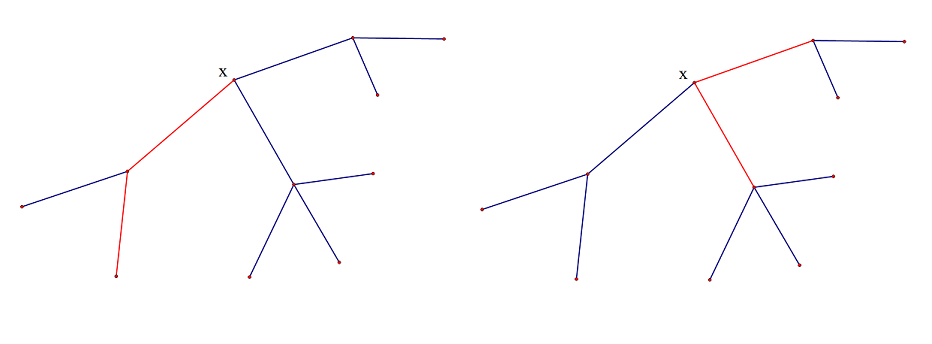
那么，只要我们找到\(x\)，就可以统计这样的一些路径了，然后……如何找到\(x\)呢？

首先明白，\(x\)是不能随便找的，为了保证时间复杂度，\(x\)显然为重心最优，找重心可以用一个简单的dfs搞定

\(x\)统计完了之后呢？这棵树被分成了两个大小基本相同的子树，然后我们把子树剥离（记得是剥离）出来，作为一个子问题继续处理，这次的处理是没必要让路径经过\(x\)的（因为经过\(x\)的已经被统计完了），以此类推下去，我们发现每个点在统计答案的时候最多被经过\(\log n\)次，因此时间复杂度为\(O(n\log n)\)

好，然后我们找到\(x\)了，然后我们得到一堆以\(x\)为端点的边，然后满足条件的路径要么是以\(x\)为端点，要么是两条以\(x\)为端点的路径接到一起，如何统计？枚举，\(O(n^2)\)……

开个桶啊，\(k\)最大不会超过\(n\)（超过\(n\)直接输出0吧），对于每次分治找到的\(x\)，只需要\(O(size)\)扫一遍桶即可，复杂度依然保持在\(O(n\log n)\)（不过你要是memset清空桶那我没点办法）

然后这题就做完了，吗？有些有意思的情况诶，拼接起来的路径，要保证两端点分别在两个子树内，这好办，我们枚举分治重心的子树时，开个临时桶记录当前子树信息，在永久桶中统计答案，然后再把临时桶的信息加入永久桶中

这道题这样子没错，其他的呢？比如说我要统计路径长度小于等于\(k\)的路径数咋办？这个时候桶就没啥用了，首先记\(dis[i]\)表示分治过程中\(i\)到\(x\)的距离，然后对\(dis[]\)排个序，每当我们找到\(l\)后，可以找到一个最大的\(r\)，满足\(dis[A_l]+dis[A_r]\leqslant r\)（\(A\)是排序后的序列），那么对答案的贡献即为\(r-l+1\)

做完了？不，这样统计有点问题，答案好像多了点，如下图

我如果要统计长度\(\leqslant 4\)的路径，这样子不是把\(A\rightarrow x\rightarrow B\)给考虑了，但是，显然不对啊，这哪能叫\(A\rightarrow B\)的简单路径啊。因此我们发现，我们将一些端点在同一颗子树内的路径拼接起来了！行吧，既然多统计了，我们减去它们即可

如何减去？既然是端点同在一个子树内被统计了多次，我们就从子树这里下手

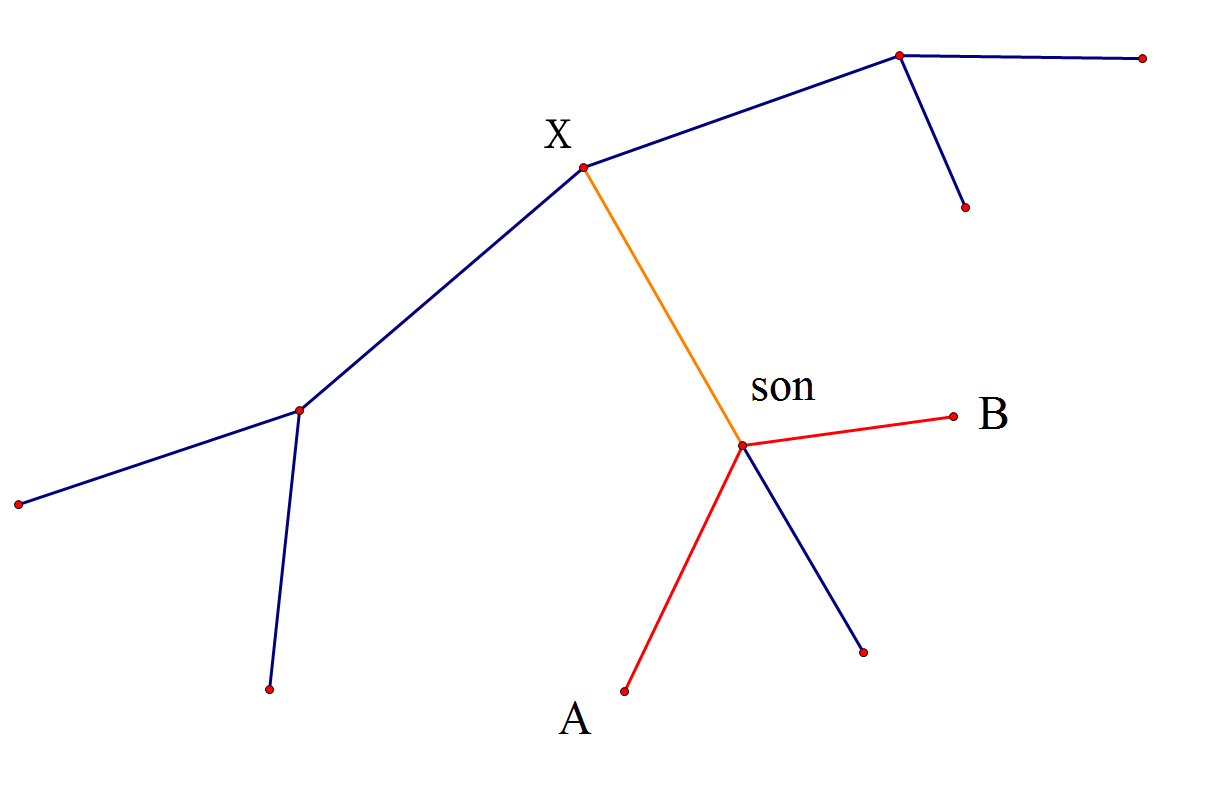
我们可以令\(son\)的权值为1，再次访问这棵子树，这样统计出来的答案，必然在\(x\)统计答案时满足两个端点同在\(son\)的子树内，我们将这样统计出来的答案减去即可

然后时间复杂度？肯定不是说桶排那个啊，那个显然\(O(n\log n)\)没得谈，我说的是后面那个，显然要快排嘛，然后时间复杂度\(O(n\log^2n)\)？但是实测起来貌似没有多多少啊？为啥？

个人理解，树上路径条数总共\(n^2\)条，每次快排之后相当于消去那些边，就算需要容斥，每条边至多被排序2次，复杂度应该依然维持在\(O(n\log n)\)级别，只是常数较大

然后就愉快的切题去吧