P3548 [POI2013] GOB-Tapestries
调了半天的逆天计算几何题。(再也不写计算几何了)
题目链接:Luogu
简化题意
多测。
给定一个多边形(不自交、任意三点不共线),多边形的每条边都有必须被照亮或不被照亮的限制,且部分照亮被视为不合法。
求多边形内是否有一个点满足在这个点上放置一个大小忽略不计的点光源,其发出的光线恰好能满足所有限制。
思路
首先考虑不能被照亮的部分。
对于一段连续的不能被照亮的区间,如图(红色表示能被照射到,黑色表示不能被照射到):
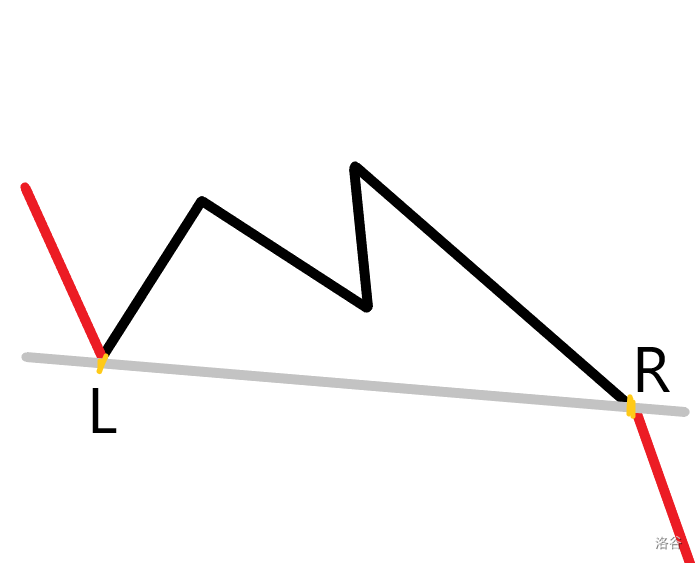
当我们连接区间的左右端点 \(L\) 和 \(R\) 后(后面两点(例如 \(x,y\))之间的边表示为 \(x\rightarrow y\)),不难发现一些无解限制:
- 如果边 \(L-1\rightarrow L\) 和边 \(R\rightarrow R+1\) 在直线 \(L\rightarrow R\) 的同侧那么一定无解。看图可以看出,点光源唯有放在 \(L-1\rightarrow L\) 和 \(R\rightarrow R+1\) 延长线的交点与其端点的连线之间的区域才能同时照亮两边,而放在那一部分区域要么不满足不照亮的部分的限制,要么会在多边形外,所以无解。
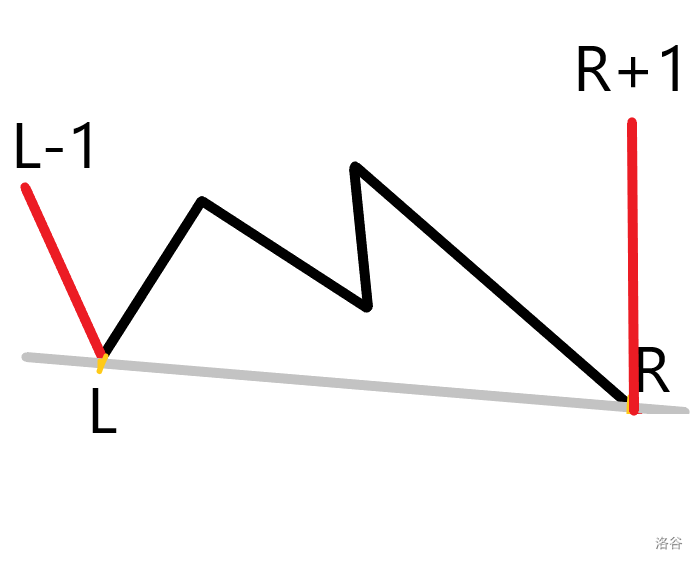
- 如果 \(L,R\) 之间的部分和直线 \(L\rightarrow R\) 有交点,无解。看图可以看出,当要同时照亮 \(L-1\rightarrow L\) 和 \(R\rightarrow R+1\) 两边时,光线会经过与未照亮部分与直线 \(L\rightarrow R\) 相交的点,所以也无解。
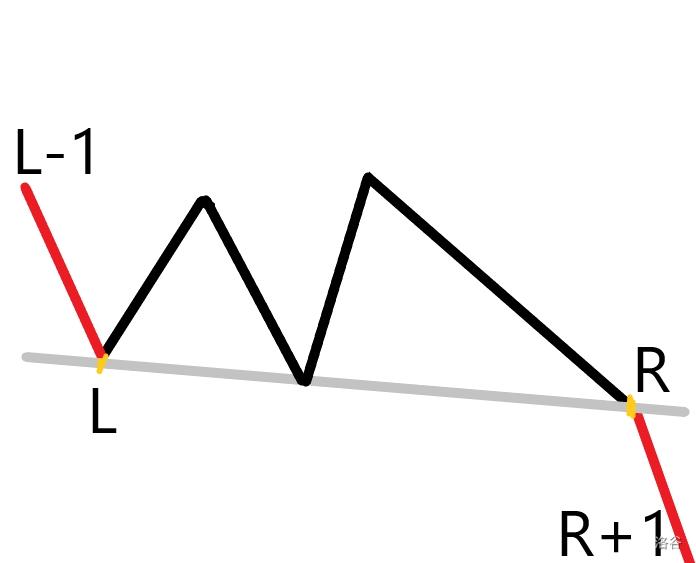
- 如果 \(L,R\) 之间的部分跨越直线 \(L\rightarrow R\),无解。理由基本同 2。
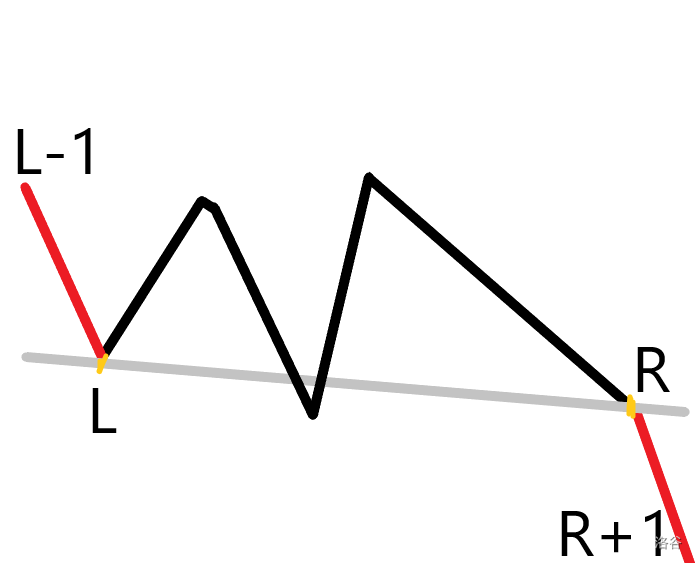
除去无解的情况,再看理应有解的第一张图,发现解应该在直线 \(L\rightarrow R\) 上,且不在线段 \(L\rightarrow R\) 上。这很好理解,在线段 \(L\rightarrow R\) 上或不在直线 \(L\rightarrow R\) 上的点一定能照亮 \(L,R\) 之间的部分,不满足条件。
对于每一段连续的不能被照亮的区间,那么解一定在所有直线 \(L\rightarrow R\) 的交集中,为一段直线或一个点。如果所有直线 \(L\rightarrow R\) 不交于一个点,无解。
对于其他应该照亮的边,每条边给当前已有解的直线或线段确定一个左端点或右端点。如果出现无解情况需特判。
如果没有不能被照亮的区间:如果有解则解一定在部分边的延长线交出来的面上。那么相当于答案点在其中一条边所在的直线上。与前面做法相同,其他每条边给当前解确定一个端点。
Code:
#include<bits/stdc++.h>
#define M 1010
#define ld long double
using namespace std;
const ld INF=1e9;
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch))x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();
return x*f;
}
inline ld readld()
{
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch))x=(x<<3)+(x<<1)+(ch^'0'),ch=getchar();
return (ld)x*f;
}
inline void write(int x)
{
if(x<0)
{
putchar('-');
write(-x);
return;
}
if(x>9)write(x/10);
putchar(x%10+48);
return;
}
struct point
{
ld x,y;
point(){}
point(ld _x,ld _y):x(_x),y(_y){}
friend point operator+(const point&p1,const point&p2)
{
point res;
res.x=p1.x+p2.x;
res.y=p1.y+p2.y;
return res;
}
friend point operator-(const point&p1,const point&p2)
{
point res;
res.x=p1.x-p2.x;
res.y=p1.y-p2.y;
return res;
}
friend ld operator^(const point&p1,const point&p2)
{
return p1.x*p2.y-p2.x*p1.y;
}
friend bool operator!=(const point&p1,const point&p2)
{
return (p1.x!=p2.x)||(p1.y!=p2.y);
}
}p[M<<1];
struct line
{
point l,r;
line(){}
line(point _l,point _r):l(_l),r(_r){}
};
vector<line>qj;
bool side_lt(point p1,point p2,point p3)
{
return ((p2-p1)^(p3-p2))>0;
}
bool cross(point p1,point p2,point p3,point p4)
{
return (side_lt(p2,p1,p3)^side_lt(p2,p1,p4))&&(side_lt(p4,p3,p1)^side_lt(p4,p3,p2));
}
ld query(point p1,point p2,point p3,point p4)
{
return ((p4-p3)^(p1-p3))/((p1-p2)^(p3-p4));
}
int n,val[M<<1];
bool check(point p1,point p2)
{
ld l=-INF,r=INF;
bool fg=0;
for(auto i:qj)
{
if(((p2-p1)^(i.r-i.l))==0)
{
if(p1!=i.l&&p2!=i.r)return 0;
}
else
{
ld x=query(p1,p2,i.l,i.r);
if(l!=-INF&&l!=x)return 0;
l=r=x;
fg=1;
}
}
for(int i=1;i<=n;++i)
if(val[i])
{
if(((p2-p1)^(p[i]-p[i+1]))==0)
{
if(((p[i+1]-p[i])^(p1-p[i]))>0)return 0;
}
else
{
ld x=query(p1,p2,p[i],p[i+1]);
if(fg&&(x==l))return 0;
if(((p2-p1)^(p[i+1]-p[i]))>0)l=max(l,x);
else r=min(r,x);
if(!fg&&l==r)return 0;
if(l>r)return 0;
}
}
return 1;
}
bool solve()
{
qj.clear();
int l=1,r,kt;
while(!val[l]&&l<=n)++l;
if(l>n)return 0;
for(r=l,kt=l;l<n+kt;l=++r)
{
if(!val[l])
{
while(!val[r])++r;
bool l_lt=side_lt(p[l-1],p[l],p[r]);
bool r_rt=side_lt(p[l],p[r],p[r+1]);
if(l_lt==r_rt)return 0;
for(int i=l+1;i<r-l;++i)if(cross(p[i],p[i+1],p[l],p[r]))return 0;
if(r>l+1)
{
if(l_lt&&side_lt(p[r],p[l],p[l-1])!=side_lt(p[r],p[l],p[l+1]))return 0;
if(r_rt&&side_lt(p[l],p[r],p[r-1])!=side_lt(p[l],p[r],p[r+1]))return 0;
}
qj.push_back(line(p[l],p[r]));
}
}
if(!qj.size())
{
for(int i=l;i<=n;++i)
if(check(p[i],p[i+1]))return 1;
return 0;
}
return check(qj[0].l,qj[0].r);
}
int main()
{
int T=read();
while(T--)
{
n=read();
for(int i=1;i<=n;++i)p[i].x=readld(),p[i].y=readld();
char s[2];
for(int i=1;i<=n;++i)scanf("%s",s),val[i]=(s[0]=='S');
for(int i=1;i<=n;++i)p[i+n]=p[i],val[i+n]=val[i];
p[0]=p[n],val[0]=val[n];
p[n<<1|1]=p[1],val[n<<1|1]=val[1];
puts(solve()?"TAK":"NIE");
}
return 0;
}






 浙公网安备 33010602011771号
浙公网安备 33010602011771号