补全 DP 优化的最后一块拼图: 降维打击
Convex_Optimisation
凸优化 (Convex Optimisation), 和凸包优化(Convex Hull Optimisation)不同, 凸包优化强调的是构造凸包, 然后求出对应斜率切线的截距, 以此来转移, 所以凸包优化又叫斜率优化.
当然这里的凸优化和数学中的凸最小化也不同, 因为数学中求的是凸函数的最小值.
动态规划的凸优化则是用二分, 二分一个惩罚值, 将 \(n\) 个元素取 \(m\) 个的最大值降维成 \(n\) 个元素取任意个的最大值的方法. 所以动态规划中的凸优化又叫带权二分.
因为是由王钦石在他的 2012 年国家集训队论文中提出的, 因此这种方法又叫 WQS 二分.
这貌似是我学的最后一种 DP 优化方式, 补全了 DP 优化的最后一张拼图. 由于凸优化是把状态降维, 不同于斜率优化和四边形不等式是优化转移, 所以我又把它称为 "降维打击".
接下来结合具体题目看一下它的应用
EPOI2018
八省 (Eight Province, EP) 联考
一棵边带权的树, 权值是或正或负的整数, 简单路径的权值是组成路径的边的权值和, 选 \(m\) 条边删除, 任意连 \(m\) 条零权边, 形成一棵新的树, 问新树的路径的最大权值.
因为节点是没有权值的, 如果已经选好了最优的断边方案, 一定可以在加边后找到一条路径, 连接所有 \(m + 1\) 个连通块, 并且权值为需要求的最大权值. 如果存在一条最大权值的路径, 它不包含连通块 \(x\) 内的点, 那么路径中一定只有 \(m - 1\) 条后来加的边, 连接了 \(m\) 个连通块. 我们把不被路径包含的那条后来加的边删掉, 连接路径末端和连通块 \(x\) 内任意一点, 组成一条长度增长 \(1\) 的路径. 因为新加的边权为 \(0\), 因此权值仍然是最大权值.
所以本题转化为将原树断成 \(m + 1\) 个连通块后, 每个连通块内选一条权值最大的路径, 然后将这 \(m + 1\) 条路径用 \(m\) 条零权边首尾相连成一条路径, 使这条路径权值最大.
最后转化为树上选 \(m + 1\) 条节点不相交的路径, 使这些路径权值和最大.
设计树形 DP, f_{i, j, 0/1/2} 表示 \(i\) 的子树中, 选 \(j\) 条节点不相交的路径的最大权值和, 最后一维为 \(0\) 表示节点 \(i\) 不被任何路径包含, 为 \(1\) 表示作为某路径端点, 为 \(2\) 表示被某路径包含但不是端点.
状态 \(O(nm)\), 转移 \(O(m)\), 总复杂度 \(O(nm^2)\) 写出来之后只能得 \(35'\), 开 -O2 可以拿到 \(60'\), LOJ 上可以拿 \(35'\), 开了 -O2 也是 \(60'\), 比 Luogu 快. 貌似比赛的时候这样写的都有 \(60'\), Day1 T3 拿到 \(60'\) 很满意了.
unsigned m, n;
unsigned A, B, D, t;
int C;
unsigned Cnt(0), Ans(0), Tmp(0);
struct Node {
Node* Fa;
vector <pair<Node*, int>> E;
long long f[105][3];
}N[300005];
inline void DFS(Node* x) {
memset(x->f, 0xaf, ((m + 1) * 3) << 3);
x->f[0][0] = x->f[1][1] = 0;
for (auto i : x->E) if (i.first != x->Fa) {
Node* Cur(i.first);
Cur->Fa = x, DFS(Cur);
for (unsigned j(m); j; --j) {
for (unsigned k(1); k <= j; ++k) {
long long Mx(max(Cur->f[k][0], max(Cur->f[k][1], Cur->f[k][2])));
if (Mx < 0) continue;
if (Cur->f[k][1] >= 0) {
x->f[j][2] = max(x->f[j][2], x->f[j - k + 1][1] + Cur->f[k][1] + i.second);
x->f[j][1] = max(x->f[j][1], x->f[j - k][0] + Cur->f[k][1] + i.second);
}
x->f[j][2] = max(x->f[j][2], x->f[j - k][2] + Mx);
x->f[j][1] = max(x->f[j][1], x->f[j - k][1] + Mx);
x->f[j][0] = max(x->f[j][0], x->f[j - k][0] + Mx);
}
}
}
}
signed main() {
n = RD(), m = RD() + 1;
for (unsigned i(1); i < n; ++i) {
A = RD(), B = RD(), C = RDsg();
N[A].E.push_back(make_pair(N + B, C));
N[B].E.push_back(make_pair(N + A, C));
}
DFS(N + 1);
printf("%lld\n", max(N[1].f[m][0], max(N[1].f[m][1], N[1].f[m][2])));
return Wild_Donkey;
}
如果我们输出大样例中, 不同的 \(m\) 下的答案, 把它们画在图像上 (图中横坐标拉长到原来的 \(1000\) 倍):
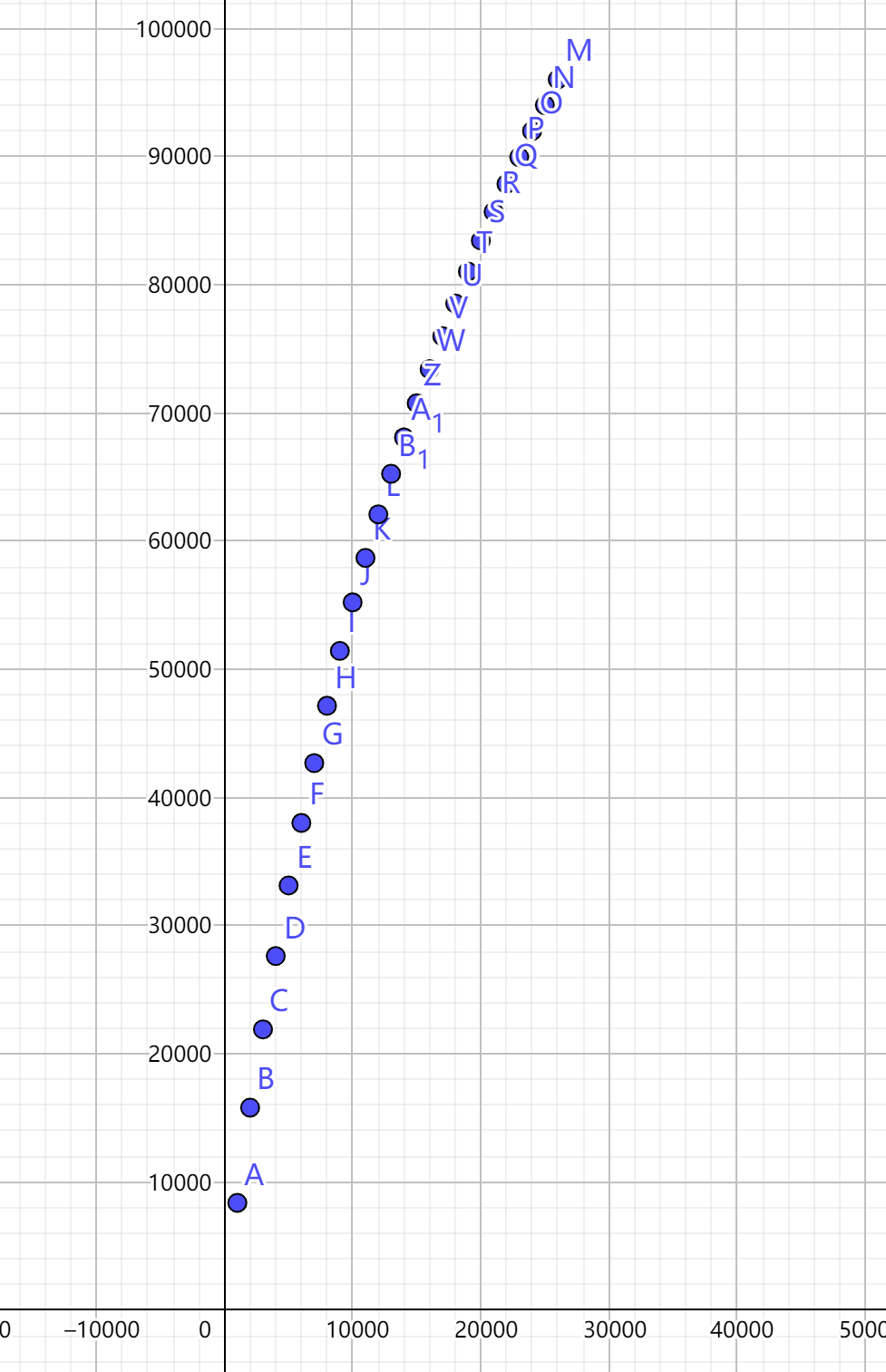
发现答案上凸 (Convex Upward), 或者说, 下凹 (Concave Downward)
去掉问题中对路径数量的限制, 将状态降维成 \(f_{i, 0/1/2}\), 表示 \(i\) 的子树中, 选择若干个节点不相交的路径, \(0/1/2\) 的意义和之前相同, 得到的最大权值和.
降维打击强就强在, 当转移需要枚举一维状态的时候, 降一维状态相当于把复杂度降了两维, 所以这样一次 DP 的时间就变成了 \(O(n)\).
如果我们记录每个状态具体选择的个数 \(g\), 那么 DP 值就变成了二元组 \((g, f)_{i, 0/1/2}\). DP 结束后, 我们就可以在上图得到一个点, 横坐标是个数, 纵坐标是权值和. 而且很显然我们求出的是上图中最高的点. (废话, 不然这个 DP 求的是什么)
当我们每增加一个新的路径, 就把答案减 \(c\), 那么我们求出的纵坐标将是 \(f - gc\) 能取到的最大值, 如果把答案加上 \(gc\), 就能得到另一个坐标. 这便是答案序列和直线 \(y = cx + b\) 的切点. 把转移方程进行细微修改:
因为答案上凸, 所以切点的横坐标一定随 \(c\) 的增加而减小, 因此我们只要二分 \(c\), 就可以求出横坐标为 \(m\) 时的纵坐标. \(c\) 的范围是 \([-nV, nV]\), 因此总复杂度是 \(O(n \log (nV))\).
不过因为答案序列也可能存在连续几个点共线的情况, 这时 \(c\) 变化 \(1\) 就会让横坐标变化不少, 不能精准定位 \(m\), 但是因为共线, 而且共线的众多点中, 两端的点是可以被二分到的, 所以直接用直线上的两点确定直线, 然后代入横坐标求值即可.
long long Ans[300005];
unsigned m, n;
unsigned A, B, D, t;
long long L(-300000000000), R(300000000000), C;
unsigned Cnt(0), Tmp(0);
struct Node {
Node* Fa;
vector <pair<Node*, int>> E;
long long f[3];
unsigned g[3];
}N[300005];
inline void DFS(Node* x) {
x->f[0] = x->g[0] = 0, x->g[1] = 1, x->f[1] = -C, x->g[2] = x->f[2] = -100000000000000000;
for (auto i : x->E) if (i.first != x->Fa) {
Node* Cur(i.first);
Cur->Fa = x, DFS(Cur);
long long Des(x->f[1] + Cur->f[1] + i.second + C);
if (Cur->f[0] > 0) x->f[2] += Cur->f[0], x->g[2] += Cur->g[0];
if (x->f[2] < Des) x->f[2] = Des, x->g[2] = x->g[1] + Cur->g[1] - 1;
if (Cur->f[0] > 0) x->f[1] += Cur->f[0], x->g[1] += Cur->g[0];
Des = x->f[0] + Cur->f[1] + i.second;
if (x->f[1] < Des) x->f[1] = Des, x->g[1] = x->g[0] + Cur->g[1];
if (Cur->f[0] > 0) x->f[0] += Cur->f[0], x->g[0] += Cur->g[0];
}
if (x->f[1] > x->f[0]) x->f[0] = x->f[1], x->g[0] = x->g[1];
if (x->f[2] > x->f[0]) x->f[0] = x->f[2], x->g[0] = x->g[2];
}
signed main() {
n = RD(), m = RD() + 1;
for (unsigned i(1); i < n; ++i) {
A = RD(), B = RD(), C = RDsg();
N[A].E.push_back(make_pair(N + B, C));
N[B].E.push_back(make_pair(N + A, C));
}
B = 0, D = n;
while (L <= R) {
C = ((L + R) >> 1);
DFS(N + 1), A = N[1].g[0];
Ans[A] = N[1].f[0] + C * A;
if (A == m) { printf("%lld\n", Ans[m]);return 0; }
if (A > m) L = C + 1, D = A;
else R = C - 1, B = A;
}
printf("%lld\n", Ans[B] + (Ans[D] - Ans[B]) / (D - B) * (m - B));
return Wild_Donkey;
}
值得注意的几点:
-
二分下界是负数.
-
如果 \(\infin\) 设置过大, 可能导致 \(-\infin + -\infin = \infin\) 出现.
-
\(\infin\) 设置过小可能导致 \(-Cg\) 比 \(-\infin\) 还要劣.
IOI2000
加强版增加了数据范围, \(O(n^2)\) 算法将无法通过此题.
仍然是把数量限制去掉来降维, 状态 \(f_i\) 表示前 \(i\) 个村庄都被覆盖, 每个邮局计算 \(c\) 的惩罚值, 到邮局的距离之和最小值. 设 \(Sum_i\) 表示前 \(i\) 个村庄的坐标之和.
根据原版可知, 这个 DP 具有决策单调性, 所以我们可以记录每个状态可以作为哪个区间的最优决策来 \(O(n\log n)\) 来做. 因为在 \(m\) 不同时, 答案是下凸的, 所以如果二分 \(C\), 就可以求出在不同乘法值下的最小花费和对应的邮局数量, 且邮局数量随着 \(C\) 的增加单调不增, 最后可以得到 \(m\) 个邮局对应的答案. \(C\) 的范围是 \([0, \sum a]\), 复杂度 \(O(n\log n\log(\sum a))\).
unsigned long long f[500005], Sum[500005], L, R, C;
unsigned long long LAns, RAns, Ans;
unsigned Stack[500005][3], STop(0);
unsigned a[500005], g[500005], m, n;
unsigned A, B, D, t, LPos, RPos, Pos;
unsigned Cnt(0), Tmp(0);
inline unsigned long long Trans(unsigned x, unsigned y) { return f[y] + Sum[y] + Sum[x] + C - Sum[(x + y) >> 1] - Sum[(x + y + 1) >> 1]; }
inline long long Calc() {
STop = 0, Stack[++STop][0] = 1, Stack[STop][1] = n, Stack[STop][2] = 0;
for (unsigned i(1), j(1); i <= n; ++i) {
while (Stack[j][1] < i) ++j;
f[i] = Trans(i, Stack[j][2]);
g[i] = g[Stack[j][2]] + 1;
while ((STop > j) && (Trans(Stack[STop][0], Stack[STop][2]) >= Trans(Stack[STop][0], i))) --STop;
unsigned BL(Stack[STop][0]), BR(Stack[STop][1] + 1), BMid, Bef(Stack[STop][2]);
while (BL ^ BR) {
BMid = ((BL + BR) >> 1);
if (Trans(BMid, Bef) < Trans(BMid, i)) BL = BMid + 1;
else BR = BMid;
}
Stack[STop][1] = BL - 1;
if (BL <= n) Stack[++STop][0] = BL, Stack[STop][1] = n, Stack[STop][2] = i;
}
return f[n] - g[n] * C;
}
signed main() {
n = RD(), m = RD();
for (unsigned i(1); i <= n; ++i) a[i] = RD();
sort(a + 1, a + n + 1);
for (unsigned i(1); i <= n; ++i) Sum[i] = Sum[i - 1] + a[i];
L = 0, C = R = Sum[n], LPos = 1, RPos = n, LAns = Calc(), RAns = 0;
while (L <= R) {
C = ((L + R) >> 1);
Ans = Calc(), Pos = g[n];
if (Pos == m) { printf("%llu\n", Ans);return 0; }
if (Pos < m) R = C - 1, LPos = Pos, LAns = Ans;
else L = C + 1, RPos = Pos, RAns = Ans;
}
printf("%llu\n", LAns - (LAns - RAns) / (RPos - LPos) * (m - LPos));
return Wild_Donkey;
}
总结
其实凸优化的过程有点求导的几何意义的那种感觉了, 最后多点共线又多少带点微分中值定理的意义, 所以可能也可以称其为微分优化. (误




 浙公网安备 33010602011771号
浙公网安备 33010602011771号