小学二年级都能看懂的 动态规划-斜率优化学习笔记

2022.10.18 update:修改了题面错误，并增加了代码

---

本文主要参考oi-wiki 斜率优化

引入

有 \(n\) 个玩具，第 \(i\) 个玩具价值为 \(c_i\)。要求将这 \(n\) 个玩具排成一排，分成若干段。对于一段 \([l,r]\)，它的代价为 \((r-l+\sum_{i=l}^{r}c_i-L)^2\) 。其中 \(L\) 是一个常量，求分段的最小代价。
\(1\leq n\leq 5\times10^5\)

很显然，这道题可以用简单的dp实现

设 \(f_i\) 为分到第 \(i\) 个点时最小代价，显然转移方程为：
\(f_i=min_{j<i} \{ f_{j-1}+(i-j+\sum_{k=j}^{i}c_k-L)^2 \}\)

即使使用前缀和来维护 \(\sum_{k=j}^{i}c_k\) 时间复杂度仍然为 \(\Theta(n^2)\)，会挂，考虑优化

斜率优化

令 \(pre_i\) 表示前 \(i\) 个数的和，我们先把转移方程写成一个更加好看的形式：

\(f_i=min_{j\leq i} \{ f_{j-1}+(i-j+pre_i-pre_{j-1}-L)^2 \}\)

接下来就是斜率优化的具体步骤了：

1.转换问题

第一步：简化。把最外圈的 \(min\) 去掉，令 \(s_i=i+pre_i,L'=L-1\) ，转移方程变为：
\(f_i= f_{j-1}+[(pre_i+i)-(pre_{j-1}+j-1)+1-L]^2=f_{j-1}+(s_i-s_{j-1}-L')^2\)

第二步：展开，把所有不只含 \(j\) 的挪到一边，转移方程变为：
\(f_i-s_i^2-L'^2+2s_is_{j-1}+2s_iL'=f_{j-1}+s_{j-1}^2+2s_{j-1}L'\)

第三步：（应该是最难理解的一步）
在每次处理 \(f_i\) 时，令

\[k=2s_i \]

\[b=f_i-s_i^2-L'^2+2s_iL' \]

\[x_j=s_{j-1} \]

\[y_j=f_{j-1}+s_{j-1}^2-2s_{j-1}L' \]

原方程就能表示成：

\[kx_j+b=y_j \]

这非常像（就是）一个一次函数表达式

注意到：\(k=2s_i\) 与 \(s_i^2-L'^2+2s_iL'\) 对于每一个 \(i\) 都是定值，而 \(f_{}+s_{j-1}^2-2s_{j-1}L'\) 与 \(s_{j-1}\) 对于每一个 \(j\) 也是固定的（废话）

由于 \(k\) 已经确定， \(b=f_i-s_i^2-L'^2+2s_iL'\) ，即 \(b\) 越小，\(f_i\) 越小

所以原题就可以转变成：找到一组 \((x_j,y_j)\) 使得直线的截距 \(b\) 最小

2.处理

但是做完了这个之后，感觉问题不仅没有变简单，反而更复杂了更难求了……

别急，毕竟是优化，肯定是要比暴力要难处理一点的

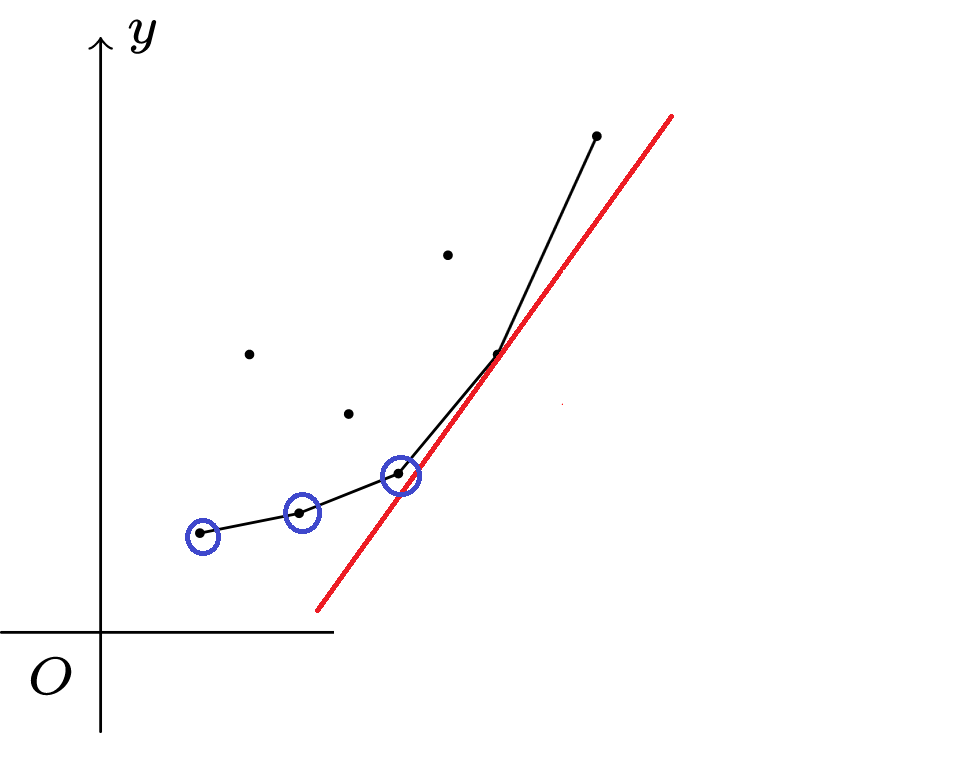
考虑如何让直线截距最小。显然，将直线一直往上移，碰到的第一个点就能让直线截距最小

观察下面一张图：

不难发现，直线可能碰到的第一个点，在所有 \((x_j,y_j)\) 构成的下凸包上，也就是说我们只需要维护下凸包即可

很显然，\(x_j=s_{j-1}=j-1+pre_{j-1}\) 单调递增，下凸包的斜率也值单调递增，也就是说，我们只需要维护一个类似单调栈的东西，保证对于栈内的任意两条直线满足 \(\forall i<j,k_i<k_j\) 即可。

更具体地讲，我们每加入一个点 \(i\) 就一直不断进行出栈，知道找到栈顶 \(top\) 使得 \(top\) 与 \(i\) 形成的直线的斜率严格大于 \(top\) 与 \(top-1\) 形成直线的斜率，再将 \(i\) 入栈即可

维护好了下凸包，怎么统计答案呢？
假设直线第一个碰到的点为 \((x_j,y_j)\)，那么在凸包上离 \(j\) 越远的点，直线肯定会越晚碰到，答案也就会更大（可以自己画图用直线切一下试试）。而 \((x_j,y_j)\) 的答案又一定会小于于其他所有点。所以我们可以从栈底开始一路往栈顶找，直到该点的答案比下一个点的答案大，这个点即为直线第一个碰到的点。而底下的点与这个点相比，只可能更劣，不可能更优，所以这些点都可以直接丢掉了

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e4+5e4;
int f[N];
int c[N],l;
int pre[N],s[N];
double stk[N];
int x[N],y[N];
int top,bot=1;//bot如果初始化为0的话，i=1时有概率出锅
int n;
double cack(int i,int j){
	return (y[i]-y[j])/double(x[i]-x[j]);
}
int cacans(int i,int j){
	return f[j-1]+(pre[i]-pre[j-1]+i-j-l)*(pre[i]-pre[j-1]+i-j-l);
}
signed main(){
	cin>>n>>l;
	for(int i=1;i<=n;i++) scanf("%lld",c+i);
	for(int i=1;i<=n;i++) pre[i]=pre[i-1]+c[i],s[i]=pre[i]+i;
	for(int i=1;i<=n;i++){
		x[i]=s[i-1],y[i]=f[i-1]+s[i-1]*s[i-1]+2*s[i-1]*(l-1); 
		while(bot<top&&cack(stk[top],stk[top-1])>cack(i,stk[top-1])) top--;
                //记得保证栈内最少有一个元素（即bot<top）
		stk[++top]=i;
		while(bot<top&&cacans(i,stk[bot])>=cacans(i,stk[bot+1])) bot++;
		f[i]=cacans(i,stk[bot]);
	}
	cout<<f[n];
}