反向传播运算
反向传播,也就是神经网络的核心算法。
在还未训练好这个神经网络的时候我们可以通过反向传播运算来训练输出我们想要的结果。
在训练神经网络的时候,我们并不能直接改变激活值,我们只能控制权重和偏置。
[赫布理论]:神经元学习的方式就是一同激活的神经元关联在一起。
实现反向传播理论:
对于如何改变倒数第二层,我们会把想改变的输出神经元的期待和其他的输出神经元全部期待加起来,作为对如何改变倒数第二层神经元的指示,这些期待的变化是对应权重的倍数,也是每个神经元激活值改变量的倍数。我们把所有期待的改变加起来,就得到了一串对倒数第二层改动的变化量。
重复这个过程改变倒数第二层神经元激活值的相关参数,把这个过程一直更换到第一层这就是反向传播
随机梯度下降:
对每个样本都进行一次反向传播,这样的计算量太大了,为了减少一些不必要的计算我们可以把训练样本打乱,然后分成或多组mimibatch,算出这个minibatch下降的一步。这就是随机梯度下降。
计算每个minibatch的梯度,调整参数不断循环,最终将会收敛到代价函数的一个局部最小值上。
反向传播的微积分原理:怎样理解链式法则?
代价函数对权重W(L)的微小变化有多敏感?
W(L)的微小变化会导致Z(L)产生一些变化,然后会导致a(L)产生变化,最终影响到代价值。
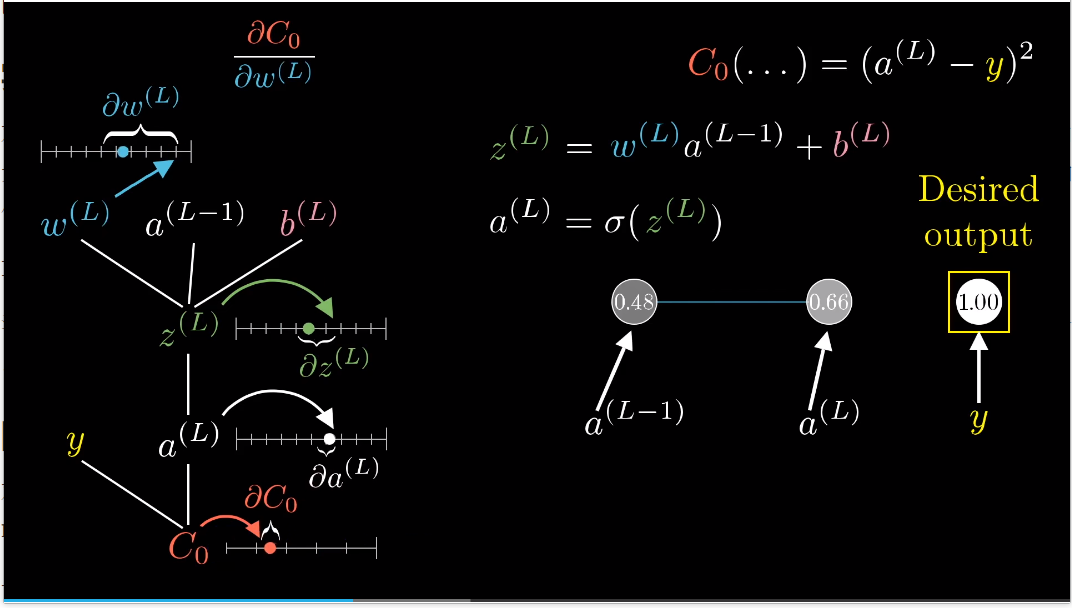
链式法则:
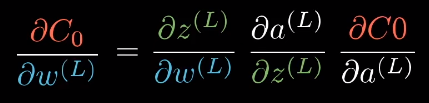
把三个比相乘,就可以得出C对W(L)的微小变化有多敏感。
然后对各个求导:导数的大小跟网络最终输出减目标结果的差成正比。(如果网络的输出差别很大,即使w稍微变一下,代价也会改变非常大)
a(L)对z(L)求导就是求sigmoid的导数或就你选择的非线性激活函数。
z(L)对w(L)求导,结果就是a(L-1)。这个权重的改变量(w求导)对最后一层的影响有多大取决于之前一层的神经元。
链式法则的第一项z对上一层激活值的敏感度就是权重w(L)。
我们可以反向应用链式法则来计算代价函数对之前的权重和偏置的敏感度。







