数据结构相关
还是决定单独拎出来写...
线段树
好像自己从来没写过动态开点(?)
动态开点
顾名思义,动态的开线段树上的节点,以达到节省空间的目的,这种技巧我们常用在普通线段树无法开下/值域过大时可以使用,动态开点线段树上的区间修改需要用到标记永久化,当然标记需要满足结合律和交换律,互相覆盖的标记是用不了的。
给一个单点加,区间查询的代码,树状数组1。
标记永久化
直接接着上文讲了,会发现,在动态开点线段树上,我们不太好维护区间加法,每次下传标记空间还是会爆掉,我们此时考虑每个点的标记不进行下传,查询时把路径上的标记再统计上即可,当然,这种思路只能适用于一些满足结合律和交换律的东西上,比如加法)。而且,这玩意不仅可以用在动态开点线段树,主席树,或者一些难以下传标记的东西里面。
一个是主席树区间加的板子,一个是标记永久化+树剖+期望,一个是树剖+动态开点线段树,从另一篇博客抄过来的啦,会补的,别急。
维护历史信息
吉老师线段树,还要维护多个信息。
线段树二分
线段每个区间上二分以处理某些问题。
李超线段树
线段树每个节点维护最优线段,以中点作为比较的依据,假设现在有两条线段 \(l_1\),\(l_2\),假如 \(l_1\) 在这个区间的中点高于 \(l_2\),那么显然他在这个区间更优,交换最优线段(默认取最大 \(y\) 值),显然这样并没有结束,继续向左右分治,重复上述过程,就能够维护这条线段,而我们需要在线段树上将这条线段拆成 \(\log\) 条,然后分别向下传递,所以插入复杂度 \(\log^2\),查询时我们考虑便利到每一个区间看看当前区间的最优线段在 \(k\) 的取值,然后取个最大值即可,挺好理解的。
依次,我们就可以维护平面内多条线段,发现斜率优化也是用这东西,所以很多斜率优化的题就可以李超树,会在 dp 专题写的。
可持久化
写完动态开点就感觉这东西很简单了,考虑我们要维护每个时间戳下的线段树,暴力建出所有线段树显然是空间爆炸的,我们可以利用动态开点,记录每棵线段树的根,分别作操作,单点修改就普通的直接修改,区间修改就需要标记永久化了,具体地,我们不进行下传标记的操作,因为这样我们的空间还是会爆炸,我们把只修改每个拆分出的小区间的标记,进而在查询时依次合并信息做到保证时间和空间复杂度。区间加板子 SP11470。
感觉现在是懂了主席树的思想了,考虑我们有一个静态区间问题,比如 P1972 [SDOI2009] HH的项链,我们要询问静态区间不同颜色数,其实可以用类似动态扫描线的做法,扔到主席树上,每个主席树维护前缀区间的信息,然后差分出答案,比方说这题我们是令答案为 \(\sum_{i=l}^{r} [las_i < l]\),然后在两棵前缀主席树上作差查询答案,其实这里的主席树就可以看做动态开点的权值线段树了。
再者就是查询区间第 \(k\) 大的问题,也是两棵权值线段树作差,然后比较左右子树的大小再向左/右,跟平衡树查询的思路是一致的。给一个裸题 P2633 Count on a tree,树剖+主席树维护 \(k\) 小值,具体来讲,我们需要维护从每个点到根的前缀主席树,然后答案就是 \(rt_u+rt_v-rt_{lca}-rt_{fa_{lca}}\),所以我们需要维护四棵主席树作差的查询 (。
练习
二分不好想到,但想到二分就秒了,首先考虑 01 序列怎么搞,排序就简单的查个数量然后直接覆盖,但是考虑怎么将原序列变成 01 序列,发现我们可以固定一个阀值,大于就 1,小于就 0,交换完成之后再查询选点的值,显然,选点最后一个为 1 的值就是答案,所以这东西是具有单调性的,可以二分,复杂度 \(O(n\log^2n)\)。
总算是填了前面的大坑,动态开点+树剖,板子题,就是注意细节,树剖都能写错我也是唐完了。
平衡树
从洛谷搬过来了。
开新坑,从寒假拖到暑假我也是无敌了。
这里统一写,平衡树的值 lazy 标记下传和线段树是基本一致的。
AVL 树
一种严格平衡的 BST,通过左旋右旋操作维护平衡因子实现平衡。这贴两张左右旋的图。毕竟这不是重点。
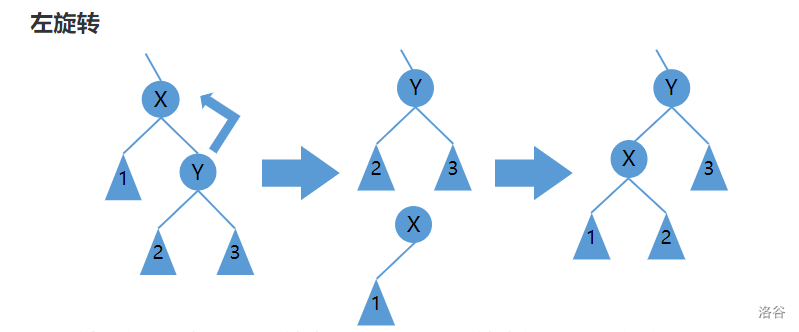
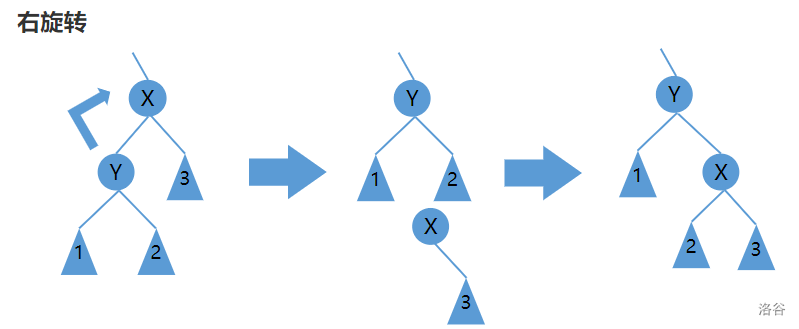
Splay 树
一种很常用的平衡树,也能用在 LCT(喜) 由于 AVL 树维护平衡因子的麻烦操作,导致的代码冗长,我们更加常用的是类似于 AVL 的 Splay 伸展树和 Treap 堆,此处先介绍 Splay。
操作
还是挨个写吧。作为伸展树的 Splay 也使用 AVL 树的左右旋操作,但是他需要再操作完成之后再将操作节点转到根,或者多转一次来降低复杂度。
- 旋转 rotate。把左右旋扔到一起做了,通过位运算实现,写一下步骤。记 \(x\),\(y\),\(z\) 分别为当前点,父亲,祖父。
- 将 \(x\) 放到原本 \(y\) 在 \(z\) 的那颗子树上,将 \(x\) 的父亲改为 \(z\)
- 假设原本 \(x\) 是 \(y\) 的右子树,那么我们把 \(x\) 的左子树挂到 \(y\) 的右子树上,把那个子树的父亲改为 \(y\)。反之亦然。
- 接上,此时我们把 \(x\) 的左子树改为 \(y\),改一下 \(y\) 的父亲。反之亦然。
- 两遍 pushup,注意还是从下往上,先 \(y\) 后 \(x\)。
inline void rotate(ll x){
ll y=tree[x].fa,z=tree[y].fa,k=tree[y].ch[1]==x;
tree[z].ch[tree[z].ch[1]==y]=x;tree[x].fa=z;
tree[y].ch[k]=tree[x].ch[k^1];tree[tree[x].ch[k^1]].fa=y;
tree[x].ch[k^1]=y;tree[y].fa=x;
pushup(y),pushup(x);
}
- splay,将某点旋转至某处,Splay的核心操作。假如当前还没有转到指定点,懒得想了,假如当前是一字型 (\(LL\) 或 \(RR\)),我们就转 \(x\),否则转 \(x\)父亲 \(y\)。假如要转到的点是根,那么将该点改成根。注意每次判断之后需要再旋转一次 \(x\)。
inline void splay(ll x,ll k){
while(tree[x].fa!=k){
ll y=tree[x].fa,z=tree[y].fa;
if(z!=k) (tree[y].ch[0]==x)^(tree[z].ch[0]==y)?rotate(x):rotate(y);
rotate(x);
}
if(!k) root=x;
}
- insert,插入操作。从一个点开始,每次按照权值向左/右找,同时记录父亲。假如碰到了空点,或者找到了有应该插入的值的点,那么跳出循环,下面判断一下是因为什么跳出的即可,新建点。最后将这个点转到根节点。
inline void insert(ll x){
ll u=root,fa=0;
while(u&&tree[u].val!=x) fa=u,u=tree[u].ch[x>tree[u].val];
if(u) tree[u].same++;
else u=++tot,tree[fa].ch[x>tree[fa].val]=u,tree[tot]={{0,0},fa,x,1,1};
splay(u,0);
}
- getx,找到权值为某值的点。由于 Splay 的特殊性质,我们反复向左/右走,路径上记录答案即可。注意结束操作之后不用 splay 一下。
inline ll getx(ll x){//找到权值为 x 的点的标号
ll u=root,ans;
while(u){
if(tree[u].val>=x) ans=u,u=tree[u].ch[0];
else u=tree[u].ch[1];
}
return ans;
}
- Next,找前驱/后继。对于找单点的前驱/后继,由于他的答案可能在父亲上面,我们要先将他旋转至根,向左向右找即可。找到答案之后 splay 一下。
inline ll Next(ll x,ll op){//找前驱,后继
ll p=getx(x);splay(p,0);
ll u=root;
if((tree[u].val>x&&op)||(tree[u].val<x&&!op)) return u;
u=tree[u].ch[op];
while(tree[u].ch[op^1]) u=tree[u].ch[op^1];
splay(u,0);
return u;
}
6.kth,找区间第 k 大。我们按照 BST 性质往左右找即可,往右找的时候减去左子树和当前点大小。最后 splay 一下降低复杂度。好像不 splay 复杂度是假的?
inline ll kth(ll x){
ll u=root;
if(tree[root].siz<x) return 0;
while(u){
if(x>tree[tree[u].ch[0]].siz+tree[u].same) x-=(tree[tree[u].ch[0]].siz+tree[u].same),u=tree[u].ch[1];
else if(tree[tree[u].ch[0]].siz>=x) u=tree[u].ch[0];
else{splay(u,0);return u;}
}
splay(x,0);
return 0;
}
- del,删除。我怎么少了一个,删除单点的话,假设我们现在要删除 \(x\),那我们找出他的前驱 \(y\),后继 \(z\),将前驱转到根节点,将后继转到 \(y\) 的右儿子,此时 \(z\) 的左儿子就是 \(x\)。直接删掉即可。
inline void del(ll x){
ll pre=Next(x,0),suf=Next(x,1);
splay(pre,0),splay(suf,pre);
ll u=tree[suf].ch[0];
if(tree[u].same>1) tree[u].same--,splay(u,0);
else tree[suf].ch[0]=0,splay(suf,0);
}
8.getk,查询排名。好像名字写错了,将他插入之后转到根,此时左儿子大小就是答案。
inline ll getk(ll x){
insert(x);
ll ans=tree[tree[root].ch[0]].siz;
del(x);
return ans;
}
-
这里再说一个操作吧,提取区间。假定现在要一个区间 \([l,r]\),我们将 \(l-1\) 转到根,\(r+1\) 转到根节点的右儿子即可,此时根节点右儿子的左子树就是要查询区间,注意,由于哨兵的影响,我们需要将下标向右移一位,就是 \(l\) 和 \(r+2\)。
-
怎么还有一个。回收内存机制,因为这种大数据结构中存在插入删除操作,假如我们反复增删,导致的下标爆炸,所以我们采用一个数组,将删掉的下标扔进去,用的时候再拿出来,就可以起到减少空间复杂度的效果。
感觉 splay 比 Treap 麻烦呢,代码还要卡常,难绷。
Treap
一种看脸的平衡树,同时满足 Tree 和 Heap 性质的平衡树。
Treap 中,每个节点有两个权值,一个 \(key\) 表示它原本的权值,我们再赋予一个 \(val\) 的随机权,令它满足大根堆的基本性质,以保证复杂度。
操作
想了想还是一边贴代码一边写吧。
- 新建。字面意思,注意 Treap 需要给随机权 \(val\)。
- 左旋。同 AVL 树的左旋操作,Treap 的左右旋分开了,感觉好理解了很多。此处设定 \(x\) 为左旋的关键点,\(u\) 为左旋关键点的右儿子,我们此处要将 \(x\) 左旋下去,或者称将 \(u\) 旋转上来。我们现将 \(u\) 的左子树挂到 \(x\) 的右子树上,再将 \(u\) 的左儿子改为 \(x\) 就结束了,注意 puhsup 时先操作下面的再操作上面的。
inline void zag(ll &x){//left
ll u=tree[x].r;
tree[x].r=tree[u].l;tree[u].l=x;x=u;
pushup(tree[x].l),pushup(x);
}
- 右旋。其实是左旋是一样。\(u\) 是 \(x\) 的左儿子,令 \(u\) 的右子树挂到 \(x\) 的左子树上即可,再传递。或者可以将左右旋操作理解为,\(u\) 和 \(x\) 交换位置,但需要换个方向,修改后 \(x\) 在 \(u\) 的哪里,就把 \(u\) 没地方放的那个子树挂过去。
inline void zig(ll &x){//right
ll u=tree[x].l;
tree[x].l=tree[u].r;tree[u].r=x,x=u;
pushup(tree[x].r),pushup(x);
}
- 建树。Treap 比较特殊的操作。依次插入哨兵,赋完随机权后,假如两个点随机权反了,就左旋一下,完事。
inline void build(){
make_node(-INF),make_node(INF);
root=1;tree[1].r=2;
pushup(root);
if(tree[1].val<tree[2].val) zag(root);
}
5.插入。由于 Treap 是同时满足 BST 和堆性质的数据结构。我们可以先按照 BST 的方式,按照大小把它插入。还是讲一下流程吧,当遍历到一个点,假如他的键值等于当前插入值,直接计数器增加,假如键值小于,往右走,大于往左走。插入之后再按照堆的性质比较,一遍遍再转上来即可,由于还是要满足 BST 的性质,所以需要全程左右旋,只要子树的 \(val\) 值大于当前点就旋转,左子树右旋,右子树左旋。(还挺异或的?)
inline void insert(ll &x,ll key){
if(!x) x=make_node(key);
else if(tree[x].key==key) tree[x].cnt++;
else if(tree[x].key>key){
insert(tree[x].l,key);
if(tree[tree[x].l].val>tree[x].val) zig(x);
}
else{
insert(tree[x].r,key);
if(tree[tree[x].r].val>tree[x].val) zag(x);
}
pushup(x);
}
6.删除。一个比较难理解的操作,但不要紧,我们分情况讨论一下,假定当前点为 \(x\)。
- 当 \(x\) 的键值大于删除的键值时,说明答案在左子树,往左走。
- 当 \(x\) 的键值小于删除的键值时,说明答案在右子树,往右走
- 当我们找到了这个键值,假如这个节点处有值,那我们也不用动了,直接删除,因为这里本来也满足平衡性。假如这个地方只有一个值,那我们 Treap 没法像 Splay 一样把他转上去删掉,我们需要把它转下去。假如这里有左子树,而且左子树的权值大于右子树的权值,那么我们右旋之后他还是可以满足性质的,我们直接右旋把当前点转下去即可。假如它不满足这个条件,我们直接给他往另一边转即可。当然,这是它不是叶子的情况,如果是叶子,直接清掉这个点就行了。
inline void del(ll &x,ll key){
if(!x) return;
if(tree[x].key==key){
if(tree[x].cnt>1) tree[x].cnt--;
else if(tree[x].l||tree[x].r){
if(!tree[x].r||tree[tree[x].l].val>tree[tree[x].r].val) zig(x),del(tree[x].r,key);
else zag(x),del(tree[x].l,key);
}
else x=0;
}
else if(tree[x].key>key) del(tree[x].l,key);
else del(tree[x].r,key);
pushup(x);
}
- 通过值查排名。其实到这就已经很 BST 了,分类讨论:
- 假如当前点是查找的 \(key\),那么他的排名就是左子树的大小 \(+1\)。
- 假如当前点的键值大于 \(key\),我们需要到左子树寻找。
- 假如当前点的键值小于 \(key\),我们需要到右子树寻找,顺便加上左子树大小和当前点相同的个数。
inline ll getrank(ll x,ll key){
if(!x) return 1;
if(tree[x].key==key) return tree[tree[x].l].siz+1;
if(tree[x].key>key) return getrank(tree[x].l,key);
return tree[tree[x].l].siz+tree[x].cnt+getrank(tree[x].r,key);
}
- 上面那个操作反过来,通过排名查值。假如左子树的大小大于 \(rank\),往左走,假如左子树大小加上当前点的个数大于等于 \(rank\) 说明这个点就是查询的点,否则就往右子树走,用 \(rank\) 减去左子树大小和这个点大小。
inline ll getkey(ll x,ll rank){
if(!x) return INF;
if(tree[tree[x].l].siz>=rank) return getkey(tree[x].l,rank);
if(tree[tree[x].l].siz+tree[x].cnt>=rank) return tree[x].key;
return getkey(tree[x].r,rank-tree[tree[x].l].siz-tree[x].cnt);
}
- 查前驱。简单函数,假如当前键值大于等于 \(key\) 说明需要往左走,否则往右走,对路径取个最小值。
inline ll getpre(ll x,ll key){
if(!x) return -INF;
if(tree[x].key>=key) return getpre(tree[x].l,key);
return max(tree[x].key,getpre(tree[x].r,key));
}
- 查后继。正好反过来,假如键值小于等于 \(key\) 说明需要往右走,否则往左走,对路径取个最大值。
inline ll getsuf(ll x,ll key){
if(!x) return INF;
if(tree[x].key<=key) return getsuf(tree[x].r,key);
return min(tree[x].key,getsuf(tree[x].l,key));
}
操作都挺短的,看代码吧,注意哨兵的影响。
FHQ-Treap
一种码量小,思想简洁的平衡树,但是没法用于 LCT 问题,通过分裂和合并来实现各种操作,跑起来好像比 Splay 要快一点。
操作
- Split 分裂。设我们将一棵树按照 \(k\) 的权值分裂,分类讨论:
- 假如 \(x\) 的权值大于 \(k\) 说明 \(x\) 的右子树一定会在拆分后的新树上,移动指针到左子树即可。
- 假如 \(x\) 的权值等于 \(k\) 说明此时 \(x\) 的左子树一定不在拆分后的树里,移动指针。
- 假如 \(x\) 的权值小于 \(k\) 说明此时 \(x\) 及其子树一定符合条件,会在拆分后的树里面,移动指针。
inline void split(ll p,ll k,ll &pl,ll &pr){
if(!p){pl = pr = 0;return;}
else if(tree[p].key <= k) pl = p,split(tree[p].r,k,tree[p].r,pr);
else pr = p,split(tree[p].l,k,pl,tree[p].l);
pushup(p);
}
- merge 合并。此时给定两棵树的指针 \(l\) 和 \(r\),\(val_i\) 表示 \(i\) 的随机权值。由于 FHQ 也要满足大根堆的性质,当考虑两棵树如何合并时,我们有限考虑他们的随机权。
- \(val_l<val_r\) 说明此时 \(l\) 的左子树不用动,往 \(l\) 的右子树走去合并即可,记得 pushup。
- \(val_r<val_l\) 说明此时 \(r\) 的左子树不用动,往 \(r\) 的左子树走去合并即可。记得 pushup。
- 假如当前某一棵树为空,直接返回另一棵树。
inline ll merge(ll pl,ll pr){
if(!pl||!pr) return pl+pr;
if(tree[pl].val<tree[pr].val){tree[pl].r=merge(tree[pl].r,pr);pushup(pl);return pl;}
else{tree[pr].l=merge(pl,tree[pr].l);pushup(pr);return pr;}
}
感觉代码还是挺简单的,其余的操作可以按照 Treap 做,或者按照 FHQ 的 Split 和 Merge 操作也是可以的。
莫队
一种离线算法,可以用 \(O(n\sqrt n)\) 的复杂度处理区间查询问题,当然,也可以带修,下文也会提到。
关于复杂度
莫队优化的关键是排序 + 分块,将每个询问离线下来,按照左端点所在块从小到大排序,假如左端点在同一个块,按照右端点从小到大排序。
处理问题时,我们可以通过移动左右端点来不断更新区间答案,而且排序后前后两个左端点的距离(移动次数)不会超过 \(2\times \sqrt n\) 次,总共 \(n\) 个查询,复杂度相乘也就是 \(O(n\sqrt n)\)。而因为右端点无序,但是固定左端的情况下按升序排列,所以因为左端有 \(O(\sqrt n)\) 块,而右端点一次移动 \(O(n)\) 次,总的也就是 \(O(n \sqrt n)\)。所以,莫队算法的总复杂度就是 \(O(n\sqrt n)\)。
其实,这种排序方式并不是最优解,最优解应该按照曼哈顿距离建最小生成树,但因为本身写这个就是暴力算法,这个也就无所谓了。
一种优化方式,奇偶性排序。在移动莫队指针的过程中,两个询问之间左右移动,可能会出现多余移动的情况,那么我们可以按照奇块正序,偶块反序的方式来排序,可以优化 30% 左右。
P1972 HH的项链
模板,开桶维护区间数个数,虽然加强了数据,卡卡也是能过的。
P1494 小 Z 的袜子
假设有 \(k\) 个相同的数,那么会有 \(\left (_{2}^{k} \right )\) 种选法,总共 \(\sum \left (_{2}^{cnt_x} \right )\) 种,\(cnt_i\) 表示 \(i\) 的数量。区间内随便选一对的方案数是 \(\left (_{2}^{r-l+1} \right )\),答案就是这俩比一下就完了,之后莫队扩缩区间维护。
P5268 [SNOI2017] 一个简单的询问
记 \(get(l,r,x)\) 表示 \([l,r]\) 区间内 \(x\) 的出现次数,求 \(\sum get(l_1,r_1,i)\times get(l_2,r_2,i)\)。
会发现这个式子很难直接推,考虑做一下差分,\(get(l_1,r_1,x)\) 可以拆成 \(get(1,r_1,x) - get(1,l_1-1,x)\)。
拓展到整个式子(令 \(g(l,x)\) 表示 \(get(1,l,x)\))
做个前缀和,就可以将整个式子当作四个询问,直接莫队统计答案即可。
P4396 [AHOI2013] 作业
这题相对于板子,只是加了个取值在 \([l,r]\) 的限制,对于这个东西,完全可以考虑树状数组,每次莫队扔进树状数组,出来直接前缀和统计答案即可。
所以 蓝 + 黄 = 紫?
复杂度 \(O(n\sqrt n\log n)\)。
带修莫队
在区间问题中,可能会存在修改操作,虽然是离线算法,但莫队也是能做的。
假设普通莫队有 \((i,j)\) 两个维度,表示区间左右端点,那我们可以再加上一维时间维 \((i,j,t)\) 表示区间在第 \(t\) 秒的答案。
P1903 数颜色 / 维护队列
以本题为例,将时间维加入排序,当作排序的第三关键字。莫队操作中,假如当前有一个修改操作,将 \(a\) 位置与 \(b\) 位置交换,将 \(a\) 位置 \(del\),将 \(b\) 位置 \(add\)。即可,反操作只是将 \(a\),\(b\) 交换。
树上莫队
现在考虑将莫队放到树上,其实直接按照欧拉序把树扔到一维平面上,欧拉序这东西就是每次深搜走到走回来都记录一下,这东西剖一下就好了,但是 \(lca\) 可能不在一段欧拉序中,所以需要特判,之后做莫队即可。
Count on a tree II
模板题。
P4074 [WC2013] 糖果公园
给定树上 \(n\) 个数,每个数有 \(w_i\) 的权值,区间内第 \(i\) 个数的价值权重是 \(v_i\),总权值定义为区间内 \(\sum w_i\times v_{cnt_i}\),每次单点修改或者查询链上价值和。
上两种莫队的综合。斯人码量题
由于是普通莫队,直接增加/减少上式即可,没什么好强调的,重点的是时间维度的意义,代表的是修改操作的下标,对应修改操作也是原树内固定的,不用再映射,注意欧拉序上的分类讨论,标记数组不要忘记。
填坑
回滚莫队
变种莫队,用于处理难以增加/删除的问题,比如区间众数,\(O(1)\) 增加,\(O(n)\) 删除,我们就可以只进行一类操作,通过回滚解决问题,这也将回滚莫队分为只增不删莫队和只删不增莫队,此处先介绍只增不删莫队。
回滚莫队的流程:
-
序列分块,划分出每个询问左右端点的所在块,通过排序使得左端点按所在块排序,右端点根据左端点升序排列。
-
分情况讨论,假如 \(l\) 和 \(r\) 在同一块内,我们可以 \(O(\sqrt n)\) 的处理询问
-
记 \(l\) 和 \(r\) 为莫队操作的区间,假如 \(l\) 和 \(r\) 不在同一块内,\(L\) 和 \(R\) 为左端点所在块的左右端点,\(x\) 和 \(y\) 为询问的左右端点。初始时,令 \(l \gets R+1\),\(r \gets R\)。
-
介于这种情况下通常认为增加是 \(O(1)\) 的,我们先移动 \(r\) 至 \(y\),记录下当前答案,然后新建变量,记录 \(l^{'}\) 向左增加的答案,之后统计答案,将 \(l\) 指针删掉来时增加的量,回到 \(R+1\),实现回滚。
-
当然,这只是一个块内询问的处理方法,假如当前询问与上一次询问不在同一块内,需要重新移动 \(l\),\(r\) 至 \(R+1\),\(R\),或许可以将这种回滚莫队看作对每个块都做一遍莫队( ? )。
AT_joisc2014_c 歴史の研究
价值定义为区间内某值出现次数与该值的乘积,每次询问求区间最大价值。
好像比板子还要板,拿这个当板子挺好。
P5906 【模板】回滚莫队&不删除莫队
定义价值为区间内相同值的下标差绝对值,求区间价值最大值。
好像没那么板了( ? ),记区间内每个值出现的最早/最晚出现的位置为 \(min_{a_i}\),\(max_{a_i}\),向右增加时,注意需要时刻更改 \(max_i\),在回滚时,假如当前 \(max_i = i\),说明已经找到了最靠右的位置,直接清零。
注意莫队的移动顺序和数组清理。
关于莫队的一些注意问题
记得设块长,每个题块长可能不同。
奇偶优化回滚莫队是不能用的。
注意莫队移动指针时的顺序:
while(l>q[i].l) add(--l);
while(r<q[i].r) add(++r);
while(l<q[i].l) del(l++);
while(r>q[i].r) del(r--);
也可以看 wiki 上的详解。
注意细节,经常卡卡常。
\(l=1,r=0\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号