摘要：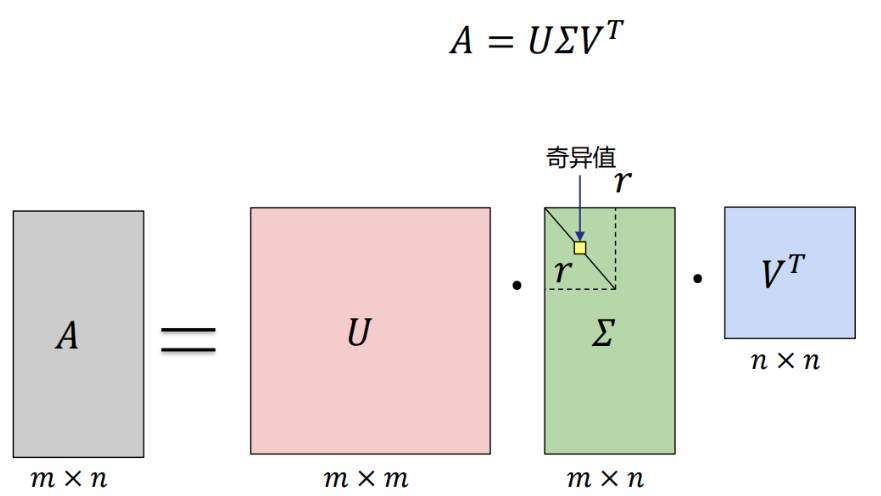 
奇异值分解已经有一百多年的历史。1873年Beltrami从双线性函数出发，引入线性变换，Beltrami 提出利用自由度使矩阵S的对角线以外的元素全部为零，即矩阵=Σ=𝑑𝑖𝑎𝑔(𝜎,𝜎,···,𝜎)为对角矩阵。于是用𝑈和𝑉分别左乘和右乘式，得到Beltrami在1873年得到的实正方矩阵的奇异值分解。1874年Jordan也独立地推导出了实正方矩阵的奇异值分解。后来，Autonne于1902年把奇异值分解推广到复正方矩阵；Eckart与Young于1936年又进一步把奇异值分解推广到一般的复长方形矩阵。 阅读全文
奇异值分解已经有一百多年的历史。1873年Beltrami从双线性函数出发，引入线性变换，Beltrami 提出利用自由度使矩阵S的对角线以外的元素全部为零，即矩阵=Σ=𝑑𝑖𝑎𝑔(𝜎,𝜎,···,𝜎)为对角矩阵。于是用𝑈和𝑉分别左乘和右乘式，得到Beltrami在1873年得到的实正方矩阵的奇异值分解。1874年Jordan也独立地推导出了实正方矩阵的奇异值分解。后来，Autonne于1902年把奇异值分解推广到复正方矩阵；Eckart与Young于1936年又进一步把奇异值分解推广到一般的复长方形矩阵。 阅读全文
posted @ 2025-10-31 19:34
丢丢八八
阅读(43)
评论(0)
推荐(0)
浙公网安备 33010602011771号