练四记录

释放囚犯

Description

Caima 王国中有一个奇怪的监狱，这个监狱一共有 \(P\) 个牢房，这些牢房一字排开，第 \(i\) 个紧挨着第 \(i+1\) 个（最后一个除外）。现在正好牢房是满的。上级下发了一个释放名单，要求每天释放名单上的一个人。现在牢房中的 \(P\) 个人，可以相互之间传话。如果某个人离开了，那么原来和这个人能说上话的人，都需要一块肉，求一共最少需要多少块肉。

Solution

很明显的区间 DP。设 \(dp_{i,j}\) 表示在 \({i,j}\) 将这个区间的人释放完最少需要块肉。转移方程和板子一样，按照题意转移即可。我写的是带记忆化搜索的分治的形式。

Code

#include<bits/stdc++.h>
#define int long long
#define N 105
using namespace std;
int n,m,x[N],ans=0x3f3f3f3f,f[N][N];
int sol(int l,int r){
	if(f[l][r])return f[l][r];
	if(r==l+1)return 0;
	int res=0x3f3f3f3f;
	for(int i=l+1;i<r;i++){
		int num=x[r]-x[l]-2+sol(l,i)+sol(i,r);
		if(res>num)res=num;
	}
	return f[l][r]=res;
}
signed main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++)cin>>x[i];
	x[m+1]=n+1;
	cout<<sol(0,m+1);
	return 0;
}

色板游戏

Description

有一个长度为 \(n\) 的色板，上面的颜色都是 1，现在有两种操作：

将区间 \([i,j]\) 全部涂成 \(c\)
求区间 \([i,j]\) 中有多少种颜色

请输出每个二操作的结果。

Solution

直接用线段树区间修改查找即可。

Code

#include<bits/stdc++.h>
#define N 100005
#define ls id<<1
#define rs id<<1|1
using namespace std;
int n,m,q,a[35];
struct node{
	int l,r,tag,c[35];
}t[N<<2];
void build(int id,int l,int r){
	t[id].l=l,t[id].r=r;
	if(l==r){
		t[id].c[1]=1;
		for(int i=2;i<=m;i++)t[id].c[i]=0;
		return;
	}
	int mid=(l+r)>>1;
	build(ls,l,mid);
	build(rs,mid+1,r);
	for(int i=1;i<=m;i++)t[id].c[i]=t[ls].c[i]+t[rs].c[i];
}
void addtag(int id,int x){
	for(int i=1;i<=m;i++)t[id].c[i]=0;
	t[id].c[x]=t[id].r-t[id].l+1;
	t[id].tag=x;
}
void pushdown(int id){
	if(t[id].tag){
		addtag(ls,t[id].tag);
		addtag(rs,t[id].tag);
		t[id].tag=0;
	}
}
void change(int id,int l,int r,int x){
	if(l<=t[id].l&&t[id].r<=r){
		addtag(id,x);
		return;
	}
	pushdown(id);
	int mid=(t[id].l+t[id].r)>>1;
	if(l<=mid)change(ls,l,r,x);
	if(r>mid)change(rs,l,r,x);
	for(int i=1;i<=m;i++)t[id].c[i]=t[ls].c[i]+t[rs].c[i];
}
void query(int id,int l,int r){
	if(l<=t[id].l&&t[id].r<=r){
		for(int i=1;i<=m;i++)a[i]+=t[id].c[i];
		return;
	}
	pushdown(id);
	int mid=(t[id].l+t[id].r)>>1;
	if(l<=mid)query(ls,l,r);
	if(r>mid)query(rs,l,r);
	for(int i=1;i<=m;i++)t[id].c[i]=t[ls].c[i]+t[rs].c[i];
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n>>m>>q;
	build(1,1,n);
	for(int i=1;i<=q;i++){
		char op;
		int l,r;
		cin>>op>>l>>r;
		if(l>r)swap(l,r);
		if(op=='C'){
			int c;
			cin>>c;
			change(1,l,r,c);
		}
		else{
			int ans=0;
			memset(a,0,sizeof a);
			query(1,l,r);
			for(int j=1;j<=m;j++)if(a[j])++ans;
			cout<<ans<<"\n";
		}
	}
	return 0;
}

小 a 和 uim 之大逃离

Description

地面上出现了一个 \(n\times m\) 的巨幅矩阵，矩阵的每个格子上有一坨 \(0\sim k\) 不等量的魔液。怪物各给了小 a 和 uim 一个魔瓶，说道，你们可以从矩阵的任一个格子开始，每次向右或向下走一步，从任一个格子结束。开始时小 a 用魔瓶吸收地面上的魔液，下一步由 uim 吸收，如此交替下去，并且要求最后一步必须由 uim 吸收。魔瓶只有 \(k\) 的容量，也就是说，如果装了 \(k+1\) 那么魔瓶会被清空成零，如果装了 \(k+2\) 就只剩下 \(1\)，依次类推。如果最后两人手中魔瓶中的魔液数量相同，就都可以活下去。现在他想知道他们都能活下来有多少种方法。

Solution

很明显的坐标 DP。设 \(dp_{i,j,k1,k2,0/1}\) 表示走到 \(i,j\) 这个位置，两人手中魔液的数量分别为 \(k1,k2\)，且这一步走的是小 a 或 uim。按照题意转移即可。然后魔瓶中魔液的数量要随时对 \(k+1\) 取模。初始化就是相当于所有位置，小 a 走，小 a 获得魔液的方案数全部初始化为 1。

因为空问题，所以需要进行滚动数组。但是因此需要在每次向下一行转移的时候重新进行初始化。最后再对取模，转移等一系列操作进行一点点小卡常即可。

Code

#include<bits/stdc++.h>
#define reg register
#define mod 1000000007
#define N 802
#define M 17
using namespace std;
int n,m,h,a[N],dp[2][N][M][M][2],ans;
inline int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while('0'<=c&&c<='9'){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
	return x*f;
}
signed main(){
	n=read(),m=read(),h=read();
	for(int i=1;i<=n;++i){
		int s=i&1;
		for(int j=1;j<=m;j++){
			a[j]=read();
			for(int k1=0;k1<=h;k1++){
				for(int k2=0;k2<=h;k2++){
					int t1=(k1-a[j])+(h+1),t2=(k2-a[j])+(h+1);
					t1-=t1>h?(h+1):0,t2-=t2>h?(h+1):0;
					dp[s][j][k1][k2][0]=dp[s][j][k1][k2][1]=0;
					if(k1==a[j]&&!k2)dp[s][j][k1][k2][0]=1;
					(dp[s][j][k1][k2][0]+=dp[!s][j][t1][k2][1])%=mod,(dp[s][j][k1][k2][1]+=dp[!s][j][k1][t2][0])%=mod;
					(dp[s][j][k1][k2][0]+=dp[s][j-1][t1][k2][1])%=mod,(dp[s][j][k1][k2][1]+=dp[s][j-1][k1][t2][0])%=mod;
					if(k1==k2)(ans+=dp[s][j][k1][k2][1])%=mod;
				}
			}
		}
	}
	printf("%d\n",ans);
	return 0;
}

树的重量

Description

P1268 树的重量

题目描述

一棵“进化树”是一个带边权的树，其叶节点表示一个物种，两个叶节点之间的距离表示两个物种的差异。现在，一个重要的问题是，根据物种之间的距离，重构相应的“进化树”。

令 \(N=\{1,2,3,\cdots ,n\}\)，用一个 \(N\) 上的矩阵 \(M\) 来定义树 \(T\)。其中，矩阵 \(M\) 满足：对于任意的 \(i\)，\(j\)，\(k\)，有 \(M[i,j]+M[j,k] \ge M[i,k]\)。树 \(T\) 满足：

叶节点属于集合 \(N\)；
边权均为非负整数；
\(d_T(i,j)=M[i,j]\)，其中 \(d_T(i,j)\) 表示树上 \(i\) 到 \(j\) 的最短路径长度。

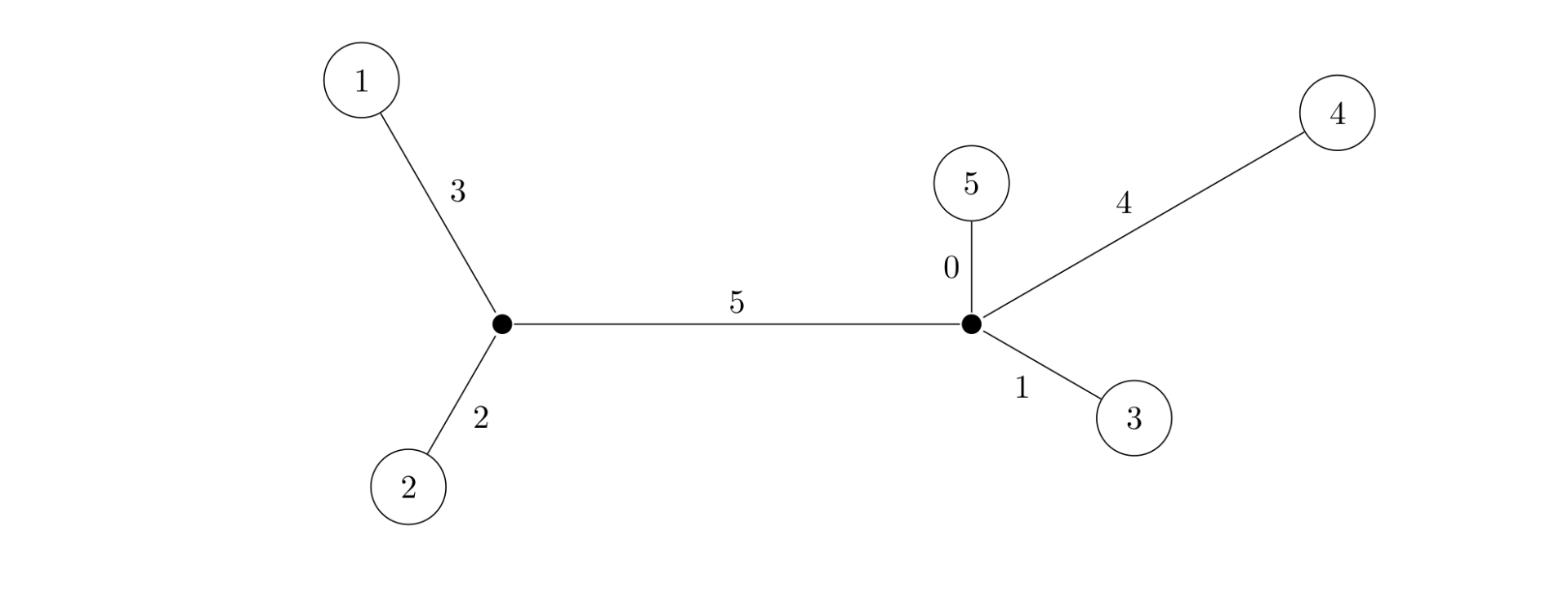
如下图，矩阵 \(M\) 描述了一棵树。

\[M=\begin{bmatrix} 0 & 5 & 9 & 12 & 8 \\ 5 & 0 & 8 & 11 & 7 \\ 9 & 8 & 0 & 5 & 1 \\ 12 & 11 & 5 & 0 & 4 \\ 8 & 7 & 1 & 4 & 0 \\ \end{bmatrix}\]

树的重量是指树上所有边权之和。对于任意给出的合法矩阵 \(M\)，它所能表示树的重量是惟一确定的，不可能找到两棵不同重量的树，它们都符合矩阵 \(M\)。请根据给出的矩阵 \(M\)，计算 \(M\) 所表示树的重量。下图是上面给出的矩阵 \(M\) 所能表示的一棵树，这棵树的总重量为 \(15\)。

Solution

我们先设 1 节点为根。我们先枚举两个叶节点：\(i,j\)。因为我们可以通过他们两个到根节点的距离，求出 \(i,j\) 分别到 \(lca(i,j)\) 的距离差，因为我们知道 \(i,j\) 之间的距离，即 \(i,j\) 分别到 \(lca(i,j)\) 的距离和。由此，我们可以得到 \(i,j\) 分别到 \(lca(i,j)\) 的距离。那么对于 \(i\) 节点而言，与它连接的最短的这个距离就是 \(i\) 到 \(i\) 的父亲节点的距离。

因为每个叶子节点都必然有一个父亲，也就是说会有一些叶子节点共同拥有一个父亲，我们将这个父亲与这些叶子节点的集合称为一个集体。那么，我们可以通过集体中的叶子节点求出两个叶子节点之间的距离，再通过这些距离，我们可以求出哪些集体可以直接相连，哪些不行。由此，我们就构造出了这样一棵完整的进化树，最后统计答案即可。

Code

#include<bits/stdc++.h>
#define int long long
#define N 35
using namespace std;
int n,dis[N][N],d[N],f[N],dist[N][N],cnt,ans,vis[N],chk[N][N];//dis是点和点的距离，dist是集合与集合的距离 
void get(int x,int y){
	int rt=1;
	while(x==rt||y==rt)++rt;
	int dt=dis[rt][x]-dis[rt][y];
	d[x]=min(d[x],(dis[x][y]+dt)/2);
	d[y]=min(d[y],(dis[x][y]-dt)/2);
}
int findf(int x){
	if(x==f[x])return x;
	return f[x]=findf(f[x]);
}
signed main(){
	cin>>n;
	for(int i=1;i<n;i++){
		for(int j=i+1;j<=n;j++){
			cin>>dis[i][j];
			dis[j][i]=dis[i][j];
		}
	}
	memset(d,0x3f,sizeof d);
	for(int i=1;i<=n;i++)f[i]=i;
	for(int i=1;i<n;i++)for(int j=i+1;j<=n;j++)get(i,j);
	for(int i=1;i<n;i++){
		for(int j=i+1;j<=n;j++){
			if(d[i]+d[j]==dis[i][j]){
				int fx=findf(i),fy=findf(j);
				if(fx!=fy)f[fx]=fy;
			}
		}
	}
	for(int i=1;i<n;i++){
		for(int j=i+1;j<=n;j++){
			int fx=findf(i),fy=findf(j);
			if(!vis[fx])++cnt,vis[fx]=1;
			if(!vis[fy])++cnt,vis[fy]=1;
			if(fx==fy||dist[fx][fy])continue;
			dist[fx][fy]=dist[fy][fx]=dis[i][j]-d[i]-d[j];
		}
	}
	for(int i=1;i<=n;i++){
		int fx=findf(i);
		for(int j=1;j<=n;j++){
			int fy=findf(j);
			if(fx==fy)continue;
			for(int k=1;k<=n;k++){
				int fz=findf(k);
				if(fx==fz||fy==fz)continue;
				if(dist[fx][fy]==dist[fx][fz]+dist[fz][fy])chk[fx][fy]=chk[fy][fx]=1;
			}
		}
	}
	for(int i=1;i<n;i++){
		for(int j=i+1;j<=n;j++){
			int fx=findf(i),fy=findf(j);
			if(chk[fx][fy]||chk[fy][fx])continue;
			--cnt;
			chk[fx][fy]=chk[fy][fx]=1;
			ans+=dist[fx][fy];
		}
	}
	for(int i=1;i<=n;i++)ans+=d[i];
	cout<<ans;
	return 0; 
}

分数排序

Description

有两个长度为 \(n\) 的数组 \(a\)，\(b\)。给你 \(q\) 个问题，每次让你求出在所有 \(\frac{a_i}{b_j}\) 中第 \(c\) 小的那个。（\(n\le 1e5\)）

Solution

现将 \(a\) 和 \(b\) 分别按从小到大和从大到小的顺序排序，然后直接通过判断有多少个数小于等于 \(mid\) 值进行实数二分。假设现在要找的答案是 \(num_c\)，那么二分要找到的就是 \(num_c\) 到 \(num_c+1\) 之间的一个数，随便是什么都行。接着我们遍历每一个 \(b\)，在对在这个 \(b\) 的前提下的 \(a\) 进行二分，即找到最大的小于这个数的值，直接输出即可。

Code

#include<bits/stdc++.h>
#define eps 1e-12
#define N 100005
#define int long long
using namespace std;
int n,m,a[N],b[N],mx;
int cmp(int a,int b){return a>b;}
int gcd(int a,int b){return b?gcd(b,a%b):a;}
int low(double a,double b){return (a<b+eps||fabs(a-b)<=eps);}

int check(double x,int c){
	int num=0,lst=n;
	for(int j=1;j<=n;j++){
		int l=1,r=lst,nw=0;
		while(l<=r){
			int i=(l+r)>>1;
			if(low(a[i]*1.0,x*b[j]))nw=i,l=i+1;
			else r=i-1;
		}
		num+=nw;
		lst=nw;
	}
	if(num==c)return 2;
	return num<=c;
}

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=1;i<=n;i++)cin>>b[i];
	sort(a+1,a+1+n);
	sort(b+1,b+1+n,cmp);
	
	for(int q=1;q<=m;q++){
		int c,ansa=1,ansb=0x3f3f3f3f;
		cin>>c;
		double l=0,r=1e6,num=eps;
		while(l<r-eps){
			double mid=(l+r)/2.0;
			int chk=check(mid,c);
			if(chk==2){
				num=mid;
				break;
			}
			if(chk)l=mid;
			else r=mid,num=mid;
		}
		for(int j=1;j<=n;j++){
			int la=1,ra=n;
			while(la<=ra){
				int i=(la+ra)>>1;
				if(low(a[i]*1.0,num*b[j])){
					la=i+1;
					if(a[i]*ansb>ansa*b[j])ansa=a[i],ansb=b[j];
				}
				else ra=i-1;
			}
		}
		int g=gcd(ansa,ansb);
		cout<<ansa/g<<" "<<ansb/g<<"\n";
	}
	return 0;
}

刷野 I

Description

Zayin 将面临 \(n\) 个站成一排的怪物，其中第 \(i\) 个怪物的生命值是 \(a_i\)。Zayin 率先使用一种攻击方式攻击，攻击过后所有血量小于等于 \(0\) 的怪物死亡。在 Zayin 攻击一次后，所有存活的怪物对 Zayin 造成 \(1\) 点伤害。以上步骤不断循环，直到 Zayin 击杀所有怪物为止。

Zayin 一共有三种攻击方式：

普通攻击: 消耗 \(0\) 点能量值，选择一只怪物并使其血量减少一点。
天音波: 消耗 \(1\) 点能量值，选择一只怪物并使其血量减少两点。
天雷破: 消耗 \(1\) 点能量值，使所有怪物血量减少一点。

现在 Zayin 一共有 \(m\) 点能量，现在他想知道在最优的策略下，击败 \(n\) 只怪物所损失的最少血量。

Solution

贪心。首先将 \(a\) 从小到大排序。我们可以得到这样一个式子：

\[ans=n\times a_1 + (n-1)\times a_2 + ... +a_n \]

对于 \(a_i\)，在 \(m\) 允许的情况下，我们有两种措施显然比较优：

直接使用天雷破把他耗死，同时对后续怪物造成伤害
使用天音波将其搞死（如果 a_i 为奇数，即无法完全杀死，还留一滴血，就再用一次天雷破）

然后我们通过杀死当前怪兽所需的时间以及对通过最开始那个式子计算后续造成的伤害进行比较，选择使用哪一种（最后大概率杀不死当前的怪兽，所以需要在用普攻将其打死，注意加上答案）。

Code

#include<bits/stdc++.h>
#define N 100005
#define int long long
using namespace std;
int n,m,d1,d2,a[N],ans;
int num(int i){
	int x=n-i+1;
	return x*(x+1)/2;
}
signed main(){
	cin>>n>>m;
	ans=-n;
	for(int i=1;i<=n;i++)cin>>a[i];
	sort(a+1,a+1+n);
	for(int i=1;i<=n;i++){
		a[i]-=d2;
		if(a[i]<=0)continue;
		int lst=m-d1-d2,k1=0,k2=0,kf=0;
		k1=min(lst,a[i]/2),k2=min(lst,a[i]);
		kf=min(lst-k1,a[i]-k1*2);
		if((k1+kf)*(n-i+1)-kf*num(i+1)+(a[i]-2*k1-kf)*(n-i+1)<=k2*(n-i+1)-k2*num(i+1)+(a[i]-k2)*(n-i+1)){
			d1+=k1,d2+=kf;
			ans+=(k1+kf)*(n-i+1);
			a[i]-=k1*2+kf;
		}
		else{
			d2+=k2;
			ans+=k2*(n-i+1);
			a[i]-=k2;
		}
		ans+=a[i]*(n-i+1);
	}
	cout<<ans;
	return 0;
}

孤独的 sxz

Description

食堂的座位可以看成一个被划分为 \(n\times m\) 的格子的矩形，长为 \(n\)，宽为 \(m\)，矩形内的每一个格子 \((i, j)(i \in [1, n], j \in [1, m])\) \((i,j\) 为整数\()\) 都是一个座位。现在，食堂里已经有了 \(k\) 个人，其中第 \(i(1 \leq i \leq k)\) 个人坐在 \((x_i, y_i)\) 处。sxz 想要找到一个座位，使得该座位与 \(k\) 个人的曼哈顿距离之和最大。请你帮他找到这个最大值。

很显然，sxz 不能和 \(\bm k\) 个人中的任何一个人坐在同一个地方。

Solution

~~根据初一绝对值知识~~，sxz坐在四个角上的值一定更大，但是因为四个角上可能有人，所以我们找四个角上的正方形中最优的那个就行了。这四个正方形的边长在 1000 左右刚好。

在求值的时候我们可以将 \(x\) 与 \(y\) 分开，然后分别排序后求前缀和。我们再使用二分查出它现在的位置，由此我们可以知道它在减去别的点的坐标时的正负形，然后用上提前处理好的前缀和即可。式子如下：

\[num=l\times i-sum_l+sum_k-sum_l-(k-l)\times i \]

其中，\(i\) 是当前的坐标，\(l\) 是左边的人数。

Code

#include<bits/stdc++.h>
#define int long long
#define N 400005
#define M 1005
using namespace std;
int n,m,t,x[N],y[N],ans,sx[N],sy[N];
map<pair<int,int>,bool>v;
int findf(int *a,int x){
	if(x>a[t])return t;
	int l=0,r=t,res=0;
	while(l<=r){
		int mid=(l+r)>>1;
		if(a[mid]<=x)res=mid,l=mid+1;
		else r=mid-1;
	}
	return res;
}
signed main(){
	cin>>n>>m>>t;
	for(int i=1;i<=t;i++)cin>>x[i]>>y[i],v[{x[i],y[i]}]=1;
	sort(x+1,x+1+t),sort(y+1,y+1+t);
	x[t+1]=n+1,y[t+1]=m+1;
	for(int i=1;i<=t;i++){
		sx[i]=sx[i-1]+x[i];
		sy[i]=sy[i-1]+y[i];
	}
	for(int i=1;i<=n&&i<=M;i++){
		for(int j=1;j<=m&&j<=M;j++){
			if(v.count({i,j}))continue;
			int nx=findf(x,i),ny=findf(y,j);
			int num=i*(2*nx-t)-sx[nx]*2+sx[t]+j*(2*ny-t)-sy[ny]*2+sy[t];
			ans=max(ans,num);
		}
		for(int j=m,ct=0;j&&ct<=M;j--,ct++){
			if(v.count({i,j}))continue;
			int nx=findf(x,i),ny=findf(y,j);
			int num=i*(2*nx-t)-sx[nx]*2+sx[t]+j*(2*ny-t)-sy[ny]*2+sy[t];
			ans=max(ans,num);
		}
	}
	for(int i=n,ct=0;i&&ct<=M;i--,ct++){
		for(int j=1;j<=m&&j<=M;j++){
			if(v.count({i,j}))continue;
			int nx=findf(x,i),ny=findf(y,j);
			int num=i*(2*nx-t)-sx[nx]*2+sx[t]+j*(2*ny-t)-sy[ny]*2+sy[t];
			ans=max(ans,num);
		}
		for(int j=m,ct=0;j&&ct<=M;j--,ct++){
			if(v.count({i,j}))continue;
			int nx=findf(x,i),ny=findf(y,j);
			int num=i*(2*nx-t)-sx[nx]*2+sx[t]+j*(2*ny-t)-sy[ny]*2+sy[t];
			ans=max(ans,num);
		}
	}
	cout<<ans;
	return 0;
}

posted @ 2025-03-29 17:31 WDY_Hodur 阅读(33) 评论(0) 收藏举报

刷新页面返回顶部

Description

Solution

Code

Description

Solution

Code

Description

Solution

Code

Description

P1268 树的重量

题目描述

Solution

Code

Description

Solution

Code

Description

Solution

Code

Description

Solution

Code

公告