数论学习之路
如果不太影响理解与运用的证明 或是我不会的证明 就都不计喽
关于整除分块我就不想写了感觉比较基础
简单题的题解我就不写喽代码到是都有
线性筛
先来说线性筛
可 \(O(n)\) 预处理积性函数
常见用法：
- \(f(1)=1\)
- \(f(p)=...\) (一般是直接赋值)
- \(f(p^k)=...\) (一般也是递推的样子)
然后处理出来 \(low_i\) 表示 \(i\) 中最小值因子的指数次幂
具体运算就可以套板子了
点击查看代码
void Euler(int n){
s[1]=low[1]=isp[1]=1;//情况1
for(int i=2;i<=n;i++){
if(!isp[i])p[++cnt]=i,low[i]=i,s[i]=;//情况2
for(int j=1;j<=cnt&&i*p[j]<=n;j++){
isp[i*p[j]]=1;
if(i%p[j]==0){
low[i*p[j]]=low[i]*p[j];
if(low[i]==i){
s[i*p[j]]=;//情况3
}else{
s[i*p[j]]=s[i/low[i]]*s[low[i]*p[j]];
}
break;
}
low[i*p[j]]=p[j],s[i*p[j]]=s[i]*s[p[j]];
}
}
}
具体题目的例子我就不放了因为后面很多代码中都有不同用法
Dirichlet 卷积
只要知道定义式就好啦
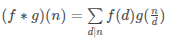
杜教筛
在 \(O(n^\frac{2}{3})\) 的时间复杂度内求积性函数前缀和
关键式子：
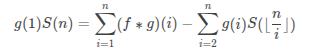
最后就是一个递归的形式，里面是整除分块
要使用线性筛预处理一部分，再用 unordered_map 做一下记忆化
写法用 \(phi\) 的前缀和举例
点击查看代码
int getphi(int n){
if(n<=N)return sp[n];//线性筛预处理的项
if(ansp[n])return ansp[n];//unordered_map记忆化
int ans=n*(n+1)/2;//计算f卷g
for(int l=2,r;l<=n;l=r+1){//整除分块
r=n/(n/l);
ans-=(r-l+1)*getphi(n/l);//递归处理
}
return ansp[n]=ans;//记忆化
}
例题：
【模板】杜教筛 这个比较简单只是用来理解原理和实现过程
对与杜教筛的第一次练习 bjzx 25-1007 模拟赛 T4 ，自己写的博客，公式推导过程挺详细的，让我理解了具体实现及推导细节，也是从这开始自己学习数论
其他题目也会有这部分内容
欧拉反演
形如这个样子
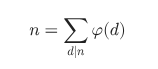
一般解决最大公因数求和问题
例题
P1447 [NOI2010] 能量采集
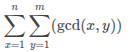
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int p[N],phi[N],cnt,sum[N];
bool isp[N];
void Euler(int n){
phi[1]=sum[1]=isp[1]=1;
for(int i=2;i<=n;i++){
if(!isp[i])p[++cnt]=i,phi[i]=i-1;
sum[i]=sum[i-1]+phi[i];
for(int j=1;j<=cnt&&i*p[j]<=n;j++){
isp[i*p[j]]=1;
if(i%p[j]==0){
phi[i*p[j]]=phi[i]*p[j];
break;
}
phi[i*p[j]]=phi[i]*phi[p[j]];
}
}
}
signed main(){
Euler(N-5);
int n,m,ans=0;
cin>>n>>m;
if(n>m)swap(n,m);
for(int l=1,r;l<=n;l=r+1){
r=min(n/(n/l),m/(m/l));
ans+=(sum[r]-sum[l-1])*(n/l)*(m/l);
}
cout<<2*ans-n*m;
}
P3768 简单的数学题
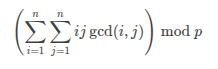
不用管%p
\[\begin{aligned}
&= \sum ^{n}_{i = 1} \sum ^{n}_{j = 1} ij \sum _{d|\gcd(i,j)} \varphi(d) \\
&= \sum ^{n}_{d=1} \varphi(d) \sum ^{\frac{n}{d}}_{i = 1} \sum ^{\frac{n}{d}}_{j = 1} ijd^2\\
&= \sum ^{n}_{d=1} d^2 \varphi(d) (\sum ^{\frac{n}{d}}_{i=1}i)^2
\end{aligned}
\]
比较有趣的一点就是1~n和的平方等于立方的和,但是对与这个式子没什么用就不写了
接下来就是整除分块套一个杜教筛
问题在于如何构造一个函数 \(h(n)\) 使得我们可以杜教筛 \(n^2 \varphi(n)\) 的前缀和
及成为一个 \(\sum_{i|n} i^2\varphi(i)*g(\frac{n}{i})\) 的形式且利于计算
很明显当 \(g(n)=n^2\) 时， 原式中 \(i^2\) 被消掉了，最后就变成了 \(n^3\)
可以杜教筛了
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e7+5;
int mod,p[N],phi[N],sum[N],cnt,inv;
bool isp[N];
unordered_map<int,int>ans;
int pow1(int x,int y){
int res=1;
while(y){
if(y&1){
res=res*x%mod;
}
x=x*x%mod;
y>>=1;
}
return res;
}
void Euler(int n){
phi[1]=sum[1]=1;
for(int i=2;i<=n;i++){
if(!isp[i])p[++cnt]=i,phi[i]=i-1;
sum[i]=(sum[i-1]+i*i%mod*phi[i]%mod)%mod;
for(int j=1;j<=cnt&&i*p[j]<=n;j++){
isp[i*p[j]]=1;
if(i%p[j]==0){
phi[i*p[j]]=phi[i]*p[j];
break;
}
phi[i*p[j]]=phi[i]*phi[p[j]];
}
}
}
int s2(int n){
n%=mod;
return n*(n+1)%mod*(2*n+1)%mod*inv%mod;
}
int s3(int n){
n%=mod;
return (n*(n+1)/2)%mod*((n*(n+1)/2)%mod)%mod;
}
int djs(int n){
if(n<=N-5)return sum[n];
if(ans[n])return ans[n];
int res=s3(n);
for(int l=2,r;l<=n;l=r+1){
r=n/(n/l);
res=(res-(s2(r)-s2(l-1)+mod)%mod*djs(n/l)%mod+mod)%mod;
}
return ans[n]=res;
}
signed main(){
int n,num=0;
cin>>mod>>n;
Euler(N-5);
inv=pow1(6,mod-2);
for(int l=1,r;l<=n;l=r+1){
r=n/(n/l);
num=(num+(djs(r)-djs(l-1)+mod)%mod*s3(n/l)%mod)%mod;
}
cout<<num<<endl;
}
莫比乌斯反演
形如
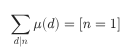
重点是艾弗森括号
例题
P2158 [SDOI2008] 仪仗队
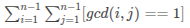
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e4+5;
int T,p[N],mu[N],cnt,sum[N],k=1;
bool isp[N];
void Euler(int n){
mu[1]=isp[1]=sum[1]=1;
for(int i=2;i<=n;i++){
if(!isp[i])p[++cnt]=i,mu[i]=-1;
sum[i]=sum[i-1]+mu[i];
for(int j=1;j<=cnt&&i*p[j]<=n;j++){
isp[i*p[j]]=1;
if(i%p[j]==0){
mu[i*p[j]]=0;
break;
}
mu[i*p[j]]=mu[i]*mu[p[j]];
}
}
}
int solve(int n,int m){
int ans=0;
n=n/k,m=m/k;
if(n>m)swap(n,m);
for(int l=1,r;l<=n;l=r+1){
r=min(n/(n/l),m/(m/l));
ans+=(sum[r]-sum[l-1])*(n/l)*(m/l);
}
return ans;
}
signed main(){
Euler(N-5);
int n;
cin>>n;
if(n==1)cout<<0<<endl;
else cout<<solve(n-1,n-1)+2<<endl;
}
P3455 [POI 2007] ZAP-Queries
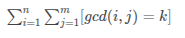
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e4+5;
int T,p[N],mu[N],cnt,sum[N];
bool isp[N];
void Euler(int n){
mu[1]=isp[1]=sum[1]=1;
for(int i=2;i<=n;i++){
if(!isp[i])p[++cnt]=i,mu[i]=-1;
sum[i]=sum[i-1]+mu[i];
for(int j=1;j<=cnt&&i*p[j]<=n;j++){
isp[i*p[j]]=1;
if(i%p[j]==0){
mu[i*p[j]]=0;
break;
}
mu[i*p[j]]=mu[i]*mu[p[j]];
}
}
}
signed main(){
Euler(N-5);
cin>>T;
while(T--){
int n,m,k,ans=0;
cin>>n>>m>>k;
n=n/k,m=m/k;
if(n>m)swap(n,m);
for(int l=1,r;l<=n;l=r+1){
r=min(n/(n/l),m/(m/l));
ans+=(sum[r]-sum[l-1])*(n/l)*(m/l);
}
cout<<ans<<endl;
}
}
P2522 [HAOI2011] Problem b
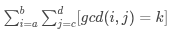
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e4+5;
int T,p[N],mu[N],cnt,sum[N],a,b,c,d,k;
bool isp[N];
void Euler(int n){
mu[1]=isp[1]=sum[1]=1;
for(int i=2;i<=n;i++){
if(!isp[i])p[++cnt]=i,mu[i]=-1;
sum[i]=sum[i-1]+mu[i];
for(int j=1;j<=cnt&&i*p[j]<=n;j++){
isp[i*p[j]]=1;
if(i%p[j]==0){
mu[i*p[j]]=0;
break;
}
mu[i*p[j]]=mu[i]*mu[p[j]];
}
}
}
int solve(int n,int m){
int ans=0;
n=n/k,m=m/k;
if(n>m)swap(n,m);
for(int l=1,r;l<=n;l=r+1){
r=min(n/(n/l),m/(m/l));
ans+=(sum[r]-sum[l-1])*(n/l)*(m/l);
}
return ans;
}
signed main(){
Euler(N-5);
cin>>T;
while(T--){
cin>>a>>b>>c>>d>>k;
cout<<solve(b,d)-solve(b,c-1)-solve(a-1,d)+solve(a-1,c-1)<<endl;
}
}
P2257 YY的GCD
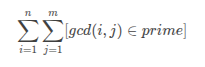
这是好题，囊括了上面所有题目
\[\begin{aligned}
&=\sum^{n}_{k=1} \sum^{n}_{i=1} \sum^{m}_{j=1}\left [ \gcd(i,j)=k \right ] (k\in \mathbb {P})\\
&=\sum^{n}_{k=1} \sum^{\left \lfloor \frac{n}{k} \right \rfloor }_{i=1} \sum^{\left \lfloor \frac{m}{k} \right \rfloor }_{j=1}\left [ \gcd(i,j)=1 \right ] (k\in \mathbb {P})\\
&=\sum^{n}_{k=1} \sum^{\left \lfloor \frac{n}{k} \right \rfloor }_{i=1} \sum^{\left \lfloor \frac{m}{k} \right \rfloor }_{j=1}\sum_{d|\gcd(i,j)}\mu(d)(k\in \mathbb {P})\\
&=\sum^{n}_{k=1} \sum^{\left \lfloor \frac{n}{k} \right \rfloor }_{d=1}\mu(d)\left \lfloor \frac{n}{kd} \right \rfloor \left \lfloor \frac{m}{kd} \right \rfloor(k\in \mathbb {P})\\
\end{aligned}
\]
设 \(T=kd\)，有
\[\begin{aligned}
&=\sum^{n}_{k=1} \sum^{\left \lfloor \frac{n}{k} \right \rfloor }_{d=1}\mu(\frac{T}{k})\left \lfloor\frac{n}{T} \right \rfloor \left \lfloor \frac{m}{T} \right \rfloor(k\in \mathbb {P})\\
&=\sum^{n}_{T=1} \left \lfloor \frac{n}{T} \right \rfloor \left \lfloor \frac{m}{T} \right \rfloor\sum_{k|T,k\in \mathbb {P}}\mu(\frac{T}{k})
\end{aligned}
\]
前面整除分块直接做做完了
问题来了
后面这部分直接算是埃氏筛复杂度有点问题，得把它融到线性筛里
然后式子我有点不会推
长这样
挖个坑以后填
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e7+5;
int T,n,m,mu[N],f[N],ans,p[N],cnt;
bool isp[N];
void Euler(int n){
mu[1]=1;
for(int i=2;i<=n;i++){
if(!isp[i])p[++cnt]=i,mu[i]=-1,f[i]=1;
for(int j=1;j<=cnt&&i*p[j]<=n;j++){
isp[i*p[j]]=1;
if(i%p[j]==0){
f[i*p[j]]=mu[i];
mu[i*p[j]]=0;
break;
}
f[i*p[j]]=mu[i]-f[i];
mu[i*p[j]]=mu[i]*mu[p[j]];
}
f[i]+=f[i-1];
}
}
signed main(){
Euler(N-5);
cin>>T;
while(T--){
cin>>n>>m;
if(n>m)swap(n,m);
ans=0;
for(int l=1,r;l<=n;l=r+1){
r=min(n/(n/l),m/(m/l));
ans+=(f[r]-f[l-1])*(n/l)*(m/l);
}
cout<<ans<<endl;
}
}
P3327 [SDOI2015] 约数个数和
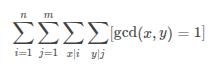
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=5e4+5;
int p[N],mu[N],cnt,T,n,m;
ll f[N];
bool isp[N];
void Euler(int n){
mu[1]=1;
for(int i=2;i<=n;i++){
if(!isp[i])p[++cnt]=i,mu[i]=-1;
for(int j=1;j<=cnt&&i*p[j]<=n;j++){
isp[i*p[j]]=1;
if(i%p[j]==0){
mu[i*p[j]]=0;
break;
}
mu[i*p[j]]=mu[i]*mu[p[j]];
}
}
}
void init(int k){
for(int n=1;n<=k;n++){
mu[n]+=mu[n-1];
for(int l=1,r;l<=n;l=r+1){
r=n/(n/l);
f[n]+=1ll*(r-l+1)*(n/l);
}
}
}
signed main(){
Euler(N-5);
init(N-5);
cin>>T;
while(T--){
cin>>n>>m;
if(n>m)swap(n,m);
ll ans=0;
for(int l=1,r;l<=n;l=r+1){
r=min(n/(n/l),m/(m/l));
ans+=1ll*(mu[r]-mu[l-1])*f[n/l]*f[m/l];
}
cout<<ans<<endl;
}
}
P1587 [NOI2016] 循环之美
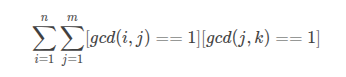
其实题意是简化过的，本来是求 \(k\) 进制下纯循环小数的个数
把它换成分数形式：\(\frac{x}{y}\) ，限制的话就是 \(gcd(x,y)=1\) （最简分数）
还有一个限制是 \(k\) 进制下，附上感性理解与严谨证明：
然后到了推式子环节
设 \(f(n,m,k)\)为上面的式子（伏笔）
则
\[\begin{aligned}
f(n,m,k)&=\sum^n_{i=1}\sum^m_{j=1}\left [ gcd(i,j)=1 \right ] \sum_{d|k}\mu(d
)\cdot \left [ d|j \right ] \\
&=\sum_{d|k}\mu(d
)\sum^n_{i=1}\sum^m_{j=1}\left [ gcd(i,j)=1 \right ] \cdot \left [ d|j \right ]
\end{aligned}
\]
令 \(j=d\cdot p\)，则
\[\begin{aligned}
&=\sum_{d|k}\mu(d)\sum^n_{i=1}\sum^{\left \lfloor \frac{m}{d} \right \rfloor }_{p=1}\left [ gcd(i,d \cdot p)=1 \right ]\\
&=\sum_{d|k}\mu(d)\sum^n_{i=1}\sum^{\left \lfloor \frac{m}{d} \right \rfloor }_{p=1}\left [ gcd(p,i)=1 \right ] \left [ gcd(i,d)=1 \right ]\\
&=\sum_{d|k}\mu(d)\sum^{\left \lfloor \frac{m}{d} \right \rfloor }_{p=1}\sum^n_{i=1}\left [ gcd(p,i)=1 \right ] \left [ gcd(i,d)=1 \right ] \\
\end{aligned}
\]
眼熟吗？
最终得到了
\[f(n,m,k)=\sum_{d|k}\mu(d)f(\left \lfloor \frac{m}{d} \right \rfloor,n,d)
\]
既然是递归那当然有边界情况
若 \(n,m\) 中有一项是 \(0\)，则最原本的式子中循环无法进行，答案为零
若 \(k=1\)，原式退化成 \(\sum^n_{i=1}\sum^m_{j=1}\left [ gcd(i,j)=1 \right ]\)
眼熟吗？
然后就没有然后了
恭喜你，暴切了 \(NOI\) \(T3\)
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e7+5;
int n,m,k,p[N],mu[N],sum[N],cnt;
bool isp[N];
unordered_map<int,int>ans;
vector<int>fac;
void Euler(int n){
mu[1]=sum[1]=1;
for(int i=2;i<=n;i++){
if(!isp[i])p[++cnt]=i,mu[i]=-1;
sum[i]=sum[i-1]+mu[i];
for(int j=1;j<=cnt&&i*p[j]<=n;j++){
isp[i*p[j]]=1;
if(i%p[j]==0){
mu[i*p[j]]=0;
break;
}
mu[i*p[j]]=mu[i]*mu[p[j]];
}
}
}
int djs(int n){
if(n<=N-5)return sum[n];
if(ans[n])return ans[n];
int res=1;
for(int l=2,r;l<=n;l=r+1){
r=n/(n/l);
res-=djs(n/l)*(r-l+1);
}
return ans[n]=res;
}
int solve(int n,int m,int k){
if(!n||!m)return 0;
int num=0;
if(k==1){
if(n>m)swap(n,m);
for(int l=1,r;l<=min(n,m);l=r+1){
r=min(n/(n/l),m/(m/l));
num+=(djs(r)-djs(l-1))*(n/l)*(m/l);
}
return num;
}
for(int i=0;i<fac.size();i++){
int v=fac[i];
if(k%v==0&&mu[v]){
num+=mu[v]*solve(m/v,n,v);
}
}
return num;
}
signed main(){
Euler(N-5);
cin>>n>>m>>k;
for(int i=1;i*i<=k;i++){
if(k%i==0){
fac.push_back(i);
if(i*i!=k){
fac.push_back(k/i);
}
}
}
cout<<solve(n,m,k);
}
exgcd
前置知识：裴蜀定理，辗转相除法
不想写那些裴蜀定理什么的了，直接拿来用吧
首先 \(exgcd\) 是用来求解二元线性丢番图方程的 这名字好装啊
说人话 并非 就是求解形如 \(ax+by=c\) 的一组解
（要求 \(\gcd(a,b)|c\) ）
我们来愉快的推式子吧！
\[\begin{aligned}
ax_1+by_1&=\gcd(a,b)\\
&=gcd(b,a\mod b)\\
&=bx_2+(a\mod b)y_2\\
\end{aligned}
\]
由于 $a\mod b=a-b\left \lfloor \frac{a}{b} \right \rfloor $
\[\begin{aligned}
ax_1+by_1&=bx_2+(a\mod b)y_2\\
&=bx_2+(a-b\left \lfloor \frac{a}{b} \right \rfloor)y_2\\
&=ay_2+b(x_2-\left \lfloor \frac{a}{b} \right \rfloor y_2)\\
\end{aligned}
\]
所以
\[x_1=y_2,y1=x_2-\left \lfloor \frac{a}{b} \right \rfloor y_2
\]
当 \(b=0\) 时, \(x\) 似乎有某种说法说可以取 \(c\) ，但是取 \(1\) 最后再转换解比较方便，\(y\) 可以取任何整数，但取 \(0\) 比较方便，并且这保证了最终得到的原方程的解不会太大，
这就是基础的 \(exgcd\)
点击查看代码
void exgcd(int a,int b,int &x,int &y){
if(!b){
x=1,y=0;
return ;
}
exgcd(b,a%b,y,x);
y-=(a/b)*x;
}
然后是求 所有解/最小最大解 的做法
从 \(ax_1+by_1=c\) 这组已求出的解出发
设 \(a(x_1+m)+b(y_1+n)=c\)
则 \(ax_1+by_1+(am+bn)=c\)
所以 \(am+bn=0\)
先设 \(d=gcd(a,b)\)
我们这一步可以构造一下
令 \(m=t\frac{b}{d},n=-t\frac{a}{d}\)
则 \(am+bn=t(\frac{ab}{d}-\frac{ab}{d})=0\)
\(t\) 越大，\(x\) 越大，\(y\) 越小
先考虑求 \(x_{min}\)
因为我们只要正整数解，所以要满足不等式组
\[\begin{cases}
x_1+t\dfrac{b}{d}\geqslant1\\
\,\\
y_1-t\dfrac{a}{d}\geqslant1
\end{cases}
\]
开解吧！
\[x_1+t\frac{b}{d}\geqslant1\\
t\frac{b}{d}\geqslant 1-x_1\\
t\geqslant \frac{d(1-x_1)}{b} \\
\,\\
\,\\
y_1-t\frac{a}{d}\geqslant1\\
-t\frac{a}{d}\geqslant 1-y_1\\
t \leqslant \frac{d(y_1-1)}{a} \\
\]
整理得
\[\begin{cases}
t\geqslant \left \lceil \frac{d(1-x_1)}{b} \right \rceil \\
\,\\
t \leqslant \left \lfloor \frac{d(y_1-1)}{a} \right \rfloor \\
\end{cases}
\]
我都多加了取整
判完无解后取对应上下界可以得出 \(x_{min}\) 与 \(y_{min}\)
\(max\) 值直接解方程出吧
例题
P5656【模板】二元一次不定方程 (exgcd)
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int T,a,b,c;
int exgcd(int a,int b,int &x,int &y){
if(b==0){
x=1,y=0;
return a;
}
int d=exgcd(b,a%b,y,x);
y-=(a/b)*x;
return d;
}
signed main(){
cin>>T;
while(T--){
cin>>a>>b>>c;
int x,y,d,m,n;
d=exgcd(a,b,x,y);//求等于gcd的一组解
if(c%d){
cout<<-1<<endl;
continue;
}
x*=c/d,y*=c/d;//求一组解
int dx=b/d,dy=a/d;
m=ceil(1.0*(1-x)/dx),n=floor(1.0*(y-1)/dy);//公式中t的上下界
if(m>n){//无正整数解
cout<<x+m*dx<<" "<<y-n*dy<<endl;
continue;
}
int minx=(x%dx-1+dx)%dx+1,miny=(y%dy-1+dy)%dy+1;
cout<<n-m+1<<" "<<minx<<" "<<miny<<" "<<(c-miny*b)/a<<" "<<(c-minx*a)/b<<endl;//max直接解方程出
}
}
10.23模拟赛T2
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int T,n,a,b,m;
void exgcd(int a,int b,int &x,int &y){
if(!b){
x=m,y=m;
return ;
}
exgcd(b,a%b,y,x);
y-=(a/b)*x;
}
signed main(){
freopen("soldier.in","r",stdin);
freopen("soldier.out","w",stdout);
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>T;
while(T--){
cin>>n>>a>>b>>m;
if(a==b){
if(m%a==0&&m/a<=n)cout<<(m/a)*2+(n-(m/a))<<endl;
else cout<<-1<<endl;
continue;
}if(a==1&&b==2){
if(2*n<m)cout<<-1<<endl;
else cout<<(m/2)*3+(m%2)*2+(n-(m/2+m%2))<<endl;
continue;
}
int d=__gcd(a,b);
a/=d,b/=d;
if(m%d){
cout<<-1<<endl;
continue;
}
m/=d;
if(n*max(a,b)<m){
cout<<-1<<endl;
continue;
}
if(a==1){
if(m/b+m%b<=n)cout<<n+m%b+m/b*2<<endl;
else cout<<-1<<endl;
continue;
}if(b==1){
if(m/a+m%a<=n)cout<<n+m/a+m%a*2<<endl;
else cout<<-1<<endl;
continue;
}
int x,y,ans=1e16;
exgcd(a,b,x,y);
x=(x%b+b)%b;
for(int i=x;i<=n&&i*a<=m;i+=b){
if(i+(m-a*i)/b<=n){
ans=min(ans,n+i+(m-a*i)/b*2);
}
}
if(ans==1e16)cout<<-1<<endl;
else cout<<ans<<endl;
}
}
exCRT
exgcd 都有了包要写 exCRT的
exCRT是用来求形如下面的同余方程组
\( \begin{cases} x \equiv a\ (mod\ n)\ \,\\ x \equiv b\ (mod\ m)\ \end{cases} \)
考虑对于两个方程组的求解，然后就能扩展到多个（两两合并即可）
转化成这种形式：
\( \begin{cases} x =k_1n+a\ \,\\ x =k_2m+b\ \end{cases} \)
合并
\( k_1n-k_2m=b-a \)
\(n,m,a,b\) 都已知，这就是标准 \(exgcd\) ,直接求出一个 \(x'\)
然后转化成同余方程
\( x \equiv x'\ (mod\ lcm(n,m)) \)
多个方程组两两合并即可，最后解直接取 \(x'\) 即可
浙公网安备 33010602011771号