递归

递归是一种广泛的算法。

其中用到了递归的数据结构和算法：DFS深度优先搜索、前中后序二叉树遍历等。

递归公式：f(n)=f(n-1)+1 其中f(1)=1

 

1.递归需要满足的三个条件

• 一个条件的解可以分解为几个子问题的解
• 这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样
• 存在递归终止条件

写递归代码的关键：

找到如何将大问题分解为小问题的规律，并基于此写出递推公式，然后再推敲出终止条件，最后将其翻译为代码

 

注：对于递推，不要试图用人脑去分解递归的每个步骤，关键是抽象出递归公式，和找到终止条件

2.递归代码要警惕堆栈溢出

我们在栈那一节有讲过，函数调用会使用栈来保存临时变量。

每调用一个函数，都会将临时变量封装为帧栈压入内存栈，等函数执行完成时，才出栈。

而系统栈或者虚拟机栈空间一般都不大。

如果递归求解的数据规模很大，调用层次很深，一直压入栈，就会有堆栈溢出的风险。

那么，要怎么避免出现堆栈溢出呢？

我们可以通过在代码中限制递归调用的最大深度的方式来解决。

就是递归调用超过一定深度之后，我们就不继续往下递归了，直接返回报错。

如下：

因为最大允许的递归深度跟当前线程剩余的栈空间大小有关，实现无法计算，所以问题并不能完全解决。

而实时计算，代码过于复杂，影响可读性。

所以如果最大深度比较小，就可以用这种方法，否则这种方法并不实用。

 

3.递归代码要警惕重复计算

如下例子：

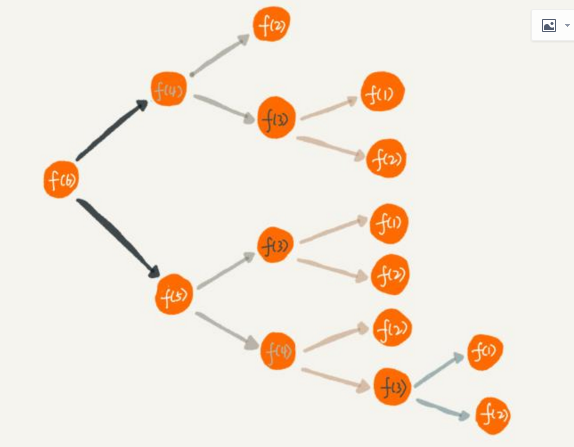
从图中，我们看出，

想要计算f(5),需要先计算f(4)和f(3),

而计算f(4)还需要计算f(3),

因此f(3)被计算了很多次，这就是重复计算问题。

 

为了避免重复问题，我们可以通过一个数据结构（比如散列表）来保存已经求解过的f(k)。

当递归调用到f(k)时，先看下是否已经求解过了。

如果是，则直接从散列表中取值返回，不需要重复计算，这样就可以避免重复计算了。

 

如下；

递归公式：f(n) = f(n-1) + f(n-2);终止条件：f(1)=1,f(2)=2;

初始代码：

避免重复之后的代码：

 

注：递归除了堆栈溢出、重复计算两个问题，还有一些其他问题。

在时间效率上，递归代码里多了很多的函数调用，

当这些函数调用的数量较大时，就会积聚成一个可观的时间成本。

在空间复杂度上，因为递归调用一次就会在内存中保存一次现场数据，

所以在分析代码空间复杂度时，需要额外考虑这部分的开销。

 

4.把递归代码改写为非递归代码

递归有利有弊；利是递归代码表达能力很强，写起来简洁；

而弊就是空间复杂度高，有堆栈溢出风险，

存在重复计算，过多的函数调用会耗时过多等问题。

 

所以，在开发过程中，我们要根据实际情况来选择是否需要用递归来实现代码。

如下：递归的代码改为非递归

 

是否所以的递归代码可以改为这种迭代循环的非递归写法呢？

笼统的讲，可以。

因为递归本身就是借助栈来实现的，只不过我们使用的栈是系统或者虚拟机本身的。

如果我们自己在内存堆上实现栈，手动模拟入栈，出栈过程，

这样任何代码都可以改写成看上去不是递归代码的样子。

但是，这种方式，实际上只是将递归改成了手动递归，本质并没变，

也没有解决前面讲到的问题，只是增加了复杂度。

 

5.如何找到最终推荐人

如下：

对于上面的代码，存在两个问题：

第一，如果递归很深，可能会有堆栈溢出的问题

第二，如果数据库存在脏数据，需要处理由此产生的无线递归问题。

 

对于第一个问题，我们可以用限制递归深度的方法解决。

对于第二个问题，也可以用限制递归深度的来解决。但是，其实还可以用自动检测“A-B-C-A”这种环的纯在。

如何检测环呢？

 

课后思考：

我们平时调试喜欢用IDE的单步跟踪功能，但是像规模比较大、递归层次很深的递归代码，几乎无法使用这种调试方式。对于递归代码，你有什么好的调试方式？