Bresenham算法理解

Bresenham

声明：本博客作者与此博客https://blog.csdn.net/cjw_soledad/article/details/78886117相同，因“博客搬家”功能效果不好，不得不重新发布

bresenham算法是计算机图形学中为了“显示器（屏幕或打印机）系由像素构成”的这个特性而设计出来的算法，使得在求直线各点的过程中全部以整数来运算，因而大幅度提升计算速度。

实现代码

这篇文章主要对下面的代码进行解释，如果能够理解下面的代码，完全可以跳过这篇文章。

// 来源:https://rosettacode.org/wiki/Bitmap/Bresenham%27s_line_algorithm#C

void line(int x0, int y0, int x1, int y1) {
 
  int dx = abs(x1-x0), sx = x0<x1 ? 1 : -1;
  int dy = abs(y1-y0), sy = y0<y1 ? 1 : -1; 
  int err = (dx>dy ? dx : -dy)/2, e2;
 
  for(;;){
    setPixel(x0,y0);
    if (x0==x1 && y0==y1) break;
    e2 = err;
    if (e2 >-dx) { err -= dy; x0 += sx; }
    if (e2 < dy) { err += dx; y0 += sy; }
  }
}

直线方程

众所周知，最基本的斜截式直线方程为\(y=kx+b(k为斜率, b为截距)\)。这个方程存在的缺点是无法表示直线\(x=\alpha\)，所以用一个新的方程来代替\(Ax+By+C=0\)。

Bresenham

Bresenham画直线的算法主要步骤是判断下一点的位置。维基百科中有一张图比较形象

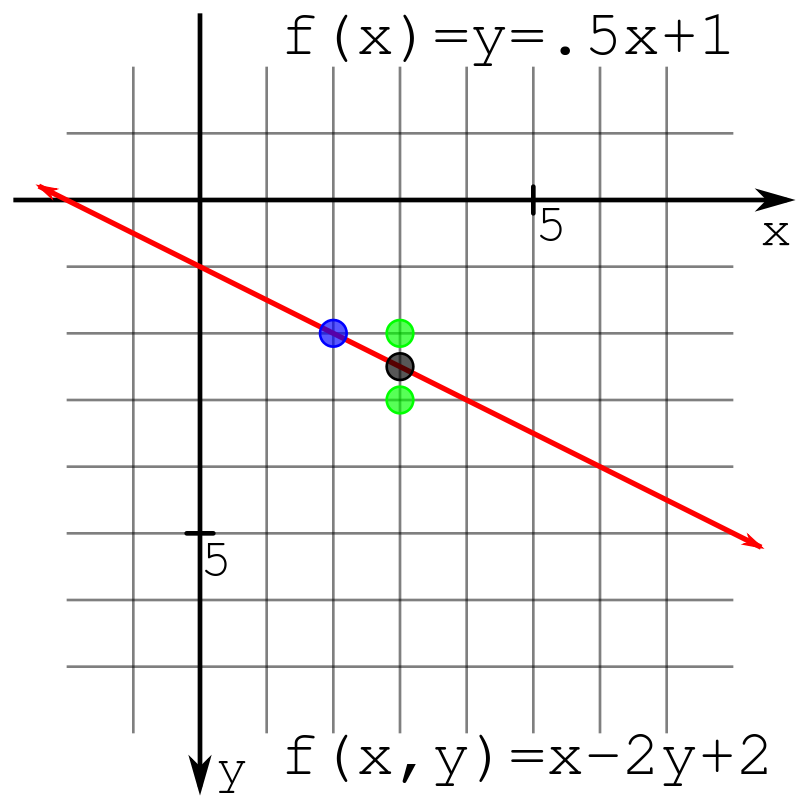
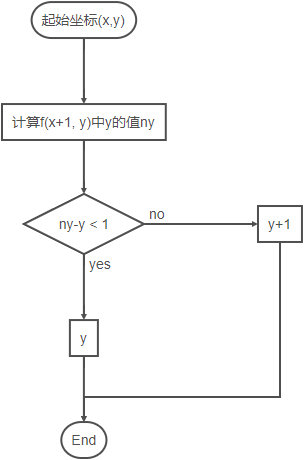
图中，每一个点代表的是一个像素，假定我们有直线\(f(x,y)\)且当前坐标为\((x,y)\)，判断下一个点的y轴坐标步骤为（如果要确定x轴坐标也类似）：

代码理解

如上面所述，我们现在能够判断直线的下一个像素点在那里了，但是Bresenham算法的优点还没有体现：我们还需要计算浮点数。为了避免浮点数计算，我们要更深入地发现划线的规律。

这里我们只考虑 \(x_1<x_2\) 并且\(y_1<y_2\)的情况，实际上我们也只需要考虑这种情况，正如前面代码所写的sx, sy，通过这两个变量我们便能控制要画的直线方向是正确的。

• Bresenham的输入为两个点\((x_1, y_1), (x_2,y_2)\)。根据这两个点，我们能够计算出两点之间的“距离“。这里的距离用的是绝对值，对应的是代码里的dx, dy。

\[\Delta x=|x_1-x_2|\\ \Delta y=|y_1-y_2| \]

根据斜截式\(y=kx+b\)，我们有\(y=\frac{\Delta y}{\Delta x}x+b\)，进而有

\[\Delta y x-\Delta x y+C = 0 \]

在这条公式中：

\[x+1 \Rightarrow y+\frac{\Delta y}{\Delta x} \\ y+1 \Rightarrow x +\frac{\Delta x}{\Delta y} \]

• 实际上，用于判断下一个点的位置的就是\(\frac{\Delta y}{\Delta x}\)和\(\frac{\Delta x}{\Delta y}\)。这两个值变化的根本目的是使上面的方程成立，根据这一点，我们直接引入一个变量\(err\)避免浮点数运算（对应代码中的err和e2）

\[\Delta y x-\Delta x y+C +err= 0 \\ x+1 \Rightarrow err-\Delta y \\ y+1 \Rightarrow err+\Delta x \]

• 现在我们已经能够将 \(err\) 和 \(x, y\) 联系起来，但是还有一个很重要的问题没有解决：判断增加x轴坐标还是增加y轴坐标
  首先假设我们在起始坐标\((x,y)\)，当前的\(err\)也是正确的，现在需要判断下一个点的坐标。
  根据传统的Bresenham算法：

\[(x+\frac{\Delta x}{\Delta y})-(x+1)>0 \Rightarrow \Delta x-\Delta y>0 \Rightarrow x+1\\ (y+\frac{\Delta y}{\Delta x})-(y+1)>0 \Rightarrow \Delta y-\Delta x>0\Rightarrow y+1 \]

我们更关注中间的部分，结合上一点所说的\(err\)和\(\Delta x,\Delta y\)的关系对其进行变形

\[ \Delta x-\Delta y>0 \Rightarrow -\Delta y>-\Delta x\\ \Delta y-\Delta x>0\Rightarrow +\Delta x < \Delta y \]

• 从上面的公式看来似乎是与\(err\)有点关系了，但是还不明确，那是因为我们的推到基于起始点，倘若基于的不是起始点，那么该公式应当为

\[ \Delta x-\Delta y>0 \Rightarrow \varepsilon -\Delta y>-\Delta x\\ \Delta y-\Delta x>0\Rightarrow \varepsilon+\Delta x < \Delta y \]

\(\varepsilon\)为一个累加值，其来源与当前点\((x,y)\)和起始点\((x_0,y_0)\)的相对位置有关，个人理解是：每一次\(x+1\)或\(y+1\)都会让原来的直线平移，这个平移便会造成误差，而这个误差会随着程序的进行而不断累加，而这个累加值对应的正是\(err\)

• 现在我们就有能力将\(err\)和程序中的err联系起来了。
  if后的条件与上面的公式对应，而err与\(\varepsilon\)不同。不同之处是：err是已经计算好的\(\varepsilon-\Delta y\)和\(\varepsilon+\Delta x\)。我们可以这样思考：在某一个点\((x,y)\)处，我们已经计算得到了正确的、可以用于判断的\(err\)，当我们选择下一个点时，我们可以顺便把下一个点的\(err\)给计算了，这就是代码中err -= dy; err += dx;蕴含的意思。

if (e2 >-dx) { err -= dy; x0 += sx; }
if (e2 < dy) { err += dx; y0 += sy; }

• 关于err的初始化 Updated in 2020

我们注意到代码中对err进行了初始化。在前面我们的推导忽略了一个部分：起始点\((x_1,y_1)\)的\(err\)。从公式\(Ax+By+C+err=0\)上看，起始点的\(err\)应当为\(0\)才对，但是代码中用了一个奇怪的值进行了初始化。看起来二者是矛盾的，但是err的初始化实际上是另一个小技巧。

int err = (dx>dy ? dx : -dy)/2

看回前面提到的那张图，蓝色点为起始点。倘若人工进行判断，我们会根据黑色点的位置\(black\)决定下一个点在何处。当\(black>0.5\)时我们会选择下面的绿点，否则选择上面的绿点。

然而此处的0.5会引入浮点数运算。我们还有一种选择：将起始点\((x_1,y_1)\)上移半个单位(这里只考虑\(\Delta x>\Delta y\)，其余情况同理)。因为起始点相对于第一个像素有了偏移，引入了误差\(err\)，根据前面对\(err\)的推导有：

\[x_1+0.5\Rightarrow err-\Delta y/2\\ y_1+0.5\Rightarrow err+\Delta x/2 \]

这样便能解释err的初始值问题，而且与我们前面的推导是一致的。

• 至此，Bresenham算法理解完成。