COMP3357 Cryptography (P2): Key Exchange progran, Public-key Encryption and Identification scheme

课程内容笔记，自用，不涉及任何 assignment，exam 答案
Notes for self-use, do not include any assignments or exams

Algorithmic Number Theory & Group Theory

在第二阶段课程的开头，将会简单的介绍一些数论与群论知识
(数论中的定理都好熟悉！但是之前都只会应用，不懂原理，认真学习一下)

Hardness 数学问题的困难性

算法数论 (Algorithmic Number Theory) 这个概念更贴近计算机领域而不是数学领域：其涉及到设计计算机算法来解决数论或者算术几何问题

对于一个数学问题，其 困难性 (hardness) 是由渐进意义下的输入 \(N\) 定义的
输入 \(N\)，一个算法的运行时间用 \(||N||\) 表示 (\(N\) 的二进制表示下的长度，因此 \(||N||=\lfloor \log N \rfloor+1\))
若某个算法的运行时间是 \(\mathtt{poly}(||N||)\) 级别的，则该数学问题是简单的

Modular Arithmetic 取模运算

• 同余: Congruency
  
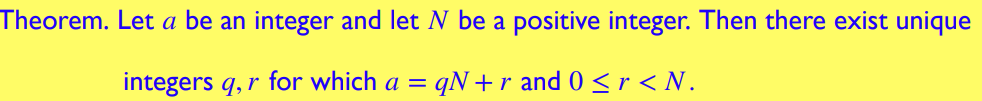
  注意 \(a=b\mod N\) 与 \(a=[b\mod N]\) 这两个 notion 的不同：后可推前，而前不可推后
  \(a=b\mod N\) 的等价描述是 \([a\mod N]=[b\mod N]\)

• 加法，减法，乘法: Addition, Substraction, Multiplication
  
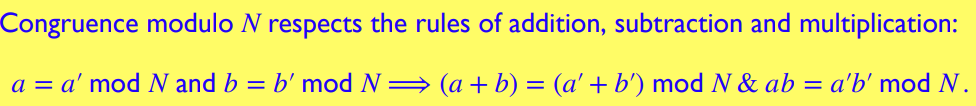
  取模运算遵循加，减，乘的对应法则
  取模运算是不遵循除法法则的：例，若 \(a=a' \mod N, b=b' \mod N\)，不能推出 \(a/b=a'/b' \mod N\)
  类似的 \(ab=ac \mod N\) 也不能推出 \(b=c \mod N\) (若 \(a\) 可逆，该式成立：在下面有相关讨论)

• 除法取模与乘法逆元: Modular Arithmetic: Division & Multiplicative Inverse
  当计算如 \([a/b\mod N]\) 的除法取模算式 (\(a\) 不能整除 \(b\)) 时，需要计算除数的乘法逆元 (Multiplicative) \(b^{-1}\)
  再对 \([ab^{-1}\mod N]\) 进行计算

  • 定义模 \(N\) 的乘法逆元：Multiplicative Inverse Modulo \(N\)
    
    乘法逆元不唯一：对于 \(b\) 的某个乘法逆元 \(c\)，所有 \(x=c\mod N\) 的 \(x\) 均可作为 \(b\) 的乘法逆元
    而 \(b^{-1}\) 特指 \(b\) 的所有模 \(N\) 乘法逆元中在 \(\{1, 2, ..., N-1\}\) 中的

  有了乘法逆元的定义，我们可以发现乘法消去律的条件是公因数 \(b\) 模 \(N\) 可逆 (invertible modulo \(N\))
  

  • 模 \(N\) 可逆 (invertible) 的条件
    
    证明见 Lec 13 Slides，需要用到一个引理 (贝祖定理) \(\gcd(a,b)=Xa+Yb\)
    其他表示方式：\(b\) 模 \(N\) 可逆 \(\iff\) \(\gcd(b,N)=1\) \(\iff\) \(b\) 与 \(N\) 互质 (relatively prime)
    根据定义我们可得出，对于某个质数 \(p\)，\(1,2,...p-1\) 都是模 \(p\) 可逆的

• 欧拉定理 Euler's Theorem
  \(a^{\phi(p)} =1 \mod p\)
  所以 \(a\times a^{\phi(p)-1}=1 \mod p\)
  \(a^{\phi(p)-1}\) 是 \(a\) 在模 \(p\) 意义下的一个乘法逆元

• 扩展欧几里得定理 eGCD: Extended Euclidean Algorithm
  根据贝祖定理，\(Xa+Yb=\gcd(a, b)\)
  扩欧算法 \(eGCD\)：输入 \(a,b\)，可计算出 \(\gcd(a,b)\) 与 \(Xa+Yb=\gcd(a,b)\) 的一个解 \((X,Y)\)
  若 \(a,b\) 互质 (relatively prime)，则有 \(Xa+Yb=1\)
  于是有 \(Xa=1\mod b\) 与 \(Yb=1 \mod a\): 可以看出 \(X\) 是 \(a\) 模 \(b\) 的乘法逆元，而 \(Y\) 是 \(b\) 模 \(a\) 的乘法逆元
  \(a^{-1}=[X \mod b]\) 且 \(b^{-1}=[Y \mod a]\)，是不是很神奇！
  因此我们可以总结，eGCD 是求正整数 \(a,b\) 的 \(\gcd\) 及其乘法逆元 (若 \(a,b\) 互质) 的算法
  至于实现，是辗转相除法的扩展：可见这篇博客，讲的很清楚 (主要是推出两个相邻辗转相除状态 \(X,Y\) 间的关系，某一层方程的解 \(X,Y\) 的上一层的解表示为 \(Y, X-Y[\frac{a}{b}]\))

算法数论 Algorithmic Number Theory

我们从算法数论角度来看各种取模运算是否 efficient

• trivial efficient computation
  
  

• 幂运算 Exponentiation

  • 整数幂运算 \(a^b\)
    \(||a^b||=O(a\cdot ||b||)\)
    整数幂运算一定不能在 \(\mathtt{polynomial}\) 时间内运行 (结果的长度都是 \(\mathtt{exponential}\) 级别的)
  • 取模幂运算 \([a^b \mod N]\)
    取模幂运算的结果的长度一定是小于 \(||N||\) 的
    trivial solution: 每乘一次 \(a\) 模一次 \(N\)，共乘 \(b\) 次：运行时间与 \(b\) 的 大小 (magnitide) 成线性 (linear)，因此与 \(b\) 的长度 \(||b||\) 成 \(\mathtt{exponential}\)
    non-trivial solution (efficient): 即经典的快速幂算法，运行时间与 \(b\) 的长度 \(||b||\) 成线性，因此与 \(b\) 的大小成 \(\mathtt{log}\)

Group 群论

相同的 mathematical structures 可以用群 (group) 进行表示

• 群 Groups
  
  一个二元运算 (binary operation)
  四个属性：Closure，Identity，Inverse，Associativity
  元素的逆元是唯一的 (unique)，每个元素唯一对应一个逆元，由此可以推出群的消去律 (Cancelation Law)
  

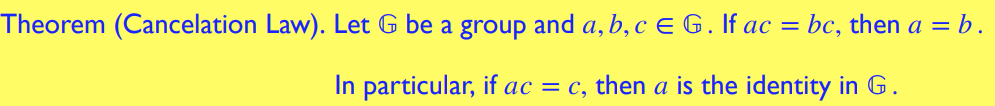
• 阿贝尔群 Abelian Groups
  
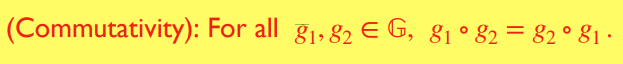
  是具有 Commutativity 属性的群
  \(\Z\) 与 \(\R\) 均是在加法下的群
  \(\Z\) 在乘法下不是群 (Inverse)，\(\R\) 在乘法下不是群 (\(0\) 这个元素没有 Inverse)：\(\R -\{0\}\) 在乘法下是群
  \(\Z_N\) 在加法模 \(N\) 下是群：该群的 order 为 \(|\Z_N|=N\)，取值只有 \(\{0,1,...,N-1\}\)
  \(\Z_N^*\) 在乘法模 \(N\) 下不是群：然而，将元素限制在模 \(N\) 可逆的范围内即可
  

• 群的加/乘法表示法
  这两种表示法只是一种写法，并不代表群的运算一定是 整数加法/乘法
  加法表示：
  运算 \(+\)，单位元 (identity element) \(0\)，\(g\) 的逆元 \(-g\)，群幂运算 (group exponential) \(m\cdot g\)
  运算 \(-\)，单位元 \(1\)，\(g\) 的逆元 \(g^{-1}\), 群幂运算 \(g^{m}\)

• 子群 Subgroups
  
  
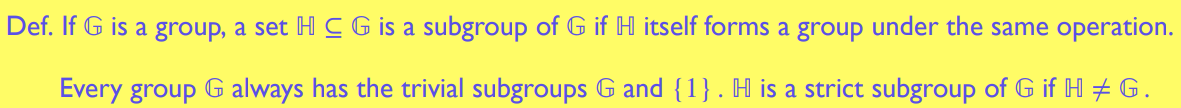
  可以想象子群在母群中相对独立且封闭

• 费马小定理 Fermat's Little Theorem
  
  证明如下：
  \(g\) 是群中任意一个元素，\(g_1, g_2, ..., g_m\) 是群中的所有元素
  由于 \(g_i\neq g_j\) for all \(i,j\)，所以 \(gg_i \neq gg_j\) for all \(i, j\)
  由于 \(gg_1, gg_2, ..., gg_n\) 是 distinct 的，根据群的 closure 性质，\(gg_1, gg_2, ..., gg_n\) 是 \(g_1, g_2, ..., g_n\) 的一个排列
  因此 \(gg_1 \cdot gg_2 \cdot ... \cdot gg_n=g_1 g_2...g_n\)
  两边消去 (根据消除率) \(g_1 g_2...g_n\)，最终有 \(g^m=1\)

  • Corollary \(1\)
    
    证明：\(x=rm+q, q<r\) 所以 \(q=[x\mod m]\)
    \(g^{x}=g^{rm+q}=(g^{m})^{r}g^{[x\mod m]}=g^{[x\mod m]}\)
  • Corollary \(2\)
    
    (1) (2) 条件等价: \(\gcd(e,m)=1\) 就意味着存在 \(d=e^{-1} \mod m\)

• 欧拉函数 Euler's Totient Functions
  欧拉函数 \(\phi(n)\) 指 \(1...n\) 中与 \(n\) 互质数的个数，即，模 \(n\) 可逆 (invertible) 的数的个数
  
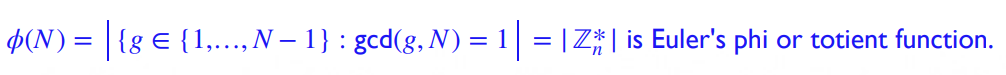
  (之前求过筛法求欧拉函数 \(\Phi(x)\) 现在有点不记得了，，找时间去复习一下)
  对于质数 \(N\)，\(\Phi(N)=N-1\)
  对于 \(N=p\cdot q\)，\(p\), \(q\) 均是大质数且 \(p\neq q\)，则有 \(\Phi(N)=(p-1)(q-1)\)
  这两个结论是显而易见的，对于质数 \(N\)，\(1...N-1\) 的所有数都与其互质
  对于 \(N=p\cdot q\)，我们减去 \(1...N-1\) 中所有 \(p\) 与 \(q\) 的倍数：\(N-1-|p, 2p, ..., (q-1)p|-|q, 2q, ..., (p-1)q|\)。这一步一定不会减去重复的数，因为 \(N=p\cdot q\) 是最小的同时是 \(p\) 与 \(q\) 倍数的数
  因此 \(\Phi(N)=N-1-(q-1)-(p-1)=pq-(p+q)+1=(p-1)(q-1)\)

  • 欧拉函数的推论：欧拉定理
    还记得 \(\Z^{*}_N\) 吗？它是指在定义在模 \(N\) 意义下乘法运算上的群, \(\Z^{*}_N:=\{b\in\{1,2,...,N-1\}|\gcd(b,N)=1\}\) (这样保证了群内的所有元素均有逆元)
    根据欧拉函数的定义，我们有 \(|\Z^{*}_N|=\Phi(N)\)
    根据费马小定理，我们有 \(g^|\Z^{*}_N|=g^{\Phi(N)}=1 \mod N, g\in Z^{*}_N\)
    若 \(N\) 是质数，则有 \(g^{\Phi(N)}=g^{N-1}=1 \mod N\)
  • 推论 \(2\):
    

Factoring problem & RSA encryption

在数论中，加法，减法，乘法，幂运算都被视作 (简单 easy)，因为都存在 efficient (solve in poly time) 的算法
而 Factoring 问题却是一个 困难 (hard) 的问题 (Factoring 可视作 Multiplying 的一个逆运算)
几个常用的 Factoring 算法：

• 朴素 Trial Division algorithm：逐个进行尝试，复杂度是指数级 (exponential time) 的 \(O(\sqrt{N}\cdot \mathtt{polylog}(N))\)
• 普通数域筛选 General Number Field Sieve (GNFS) algorithm：传统计算机所能执行的效率最高的 Factoring algorithm
• 秀尔算法 Shor's algorithm：依靠量子计算机

RSA 加密的安全性建立在 Factoring 问题的 hardness 上

• Factoring experiment
  
  
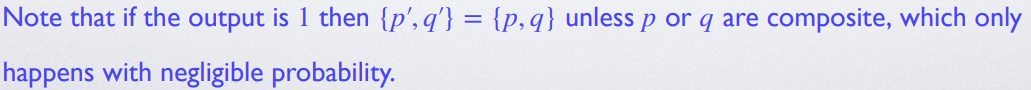
  对算法 GenModulus 而言，Factoring 是 困难 hard 的当且仅当对于任意的 PPT 敌手 \(\mathscr{A}\)
  \(\Pr[\mathtt{Factor}_{\mathscr{A}, GenModulus}(n)=1]\leq \epsilon(n)\)
  Factoring Assumption 是指，存在这样一个 GenModulus 算法，使得 Factoring 是一个 hard problem

• RSA 问题
  给出模数 (modulus) \(N\) 与整数 \(e>2\)，且 \(\gcd(e, \phi(N))=1\) (看到这个条件就要反应到这代表着 \(e\) 在模 \(\phi(N)\) 意义下可逆)
  根据费马小定理的 Corollary 2，我们知道 the exponentiation to the \(e^{th}\) power \(\mathtt{mod} \ N\) is a permutation on \(Z^*_N\)
  并且，对于 \(d=e^{-1} \mod \Phi(N)\)，那么 raising to the \(d^{th}\) power is the inverse of raising to the \(e^{th}\) power，即 \(f_d(f_e(g))=g, g\in \Z^*_N, d=e^{-1}\mod \Phi(N)\)
  对于任意 \(y\in Z_N^*\)，\([y^{e^{-1}} \mathtt{mod} \ N]\) 代表了这样一个数，其 \(e\) 次方能够恰好生成 (yields) \(y\)；或者，换一种说法，我们想要找到模 \(N\) 意义下 \(y\) 开 \(e\) 次方的根 (i.e., the \(e^{th}\) root of y \(\mathtt{mod} \ N\))

  RSA 问题指的是，给出 \(N, e, y\)，计算 \([y^{e^{-1}} \mathtt{mod} \ N]\)

• The RSA experiment
  
  定义算法 GenRSA，生成大质数 \(p,q,p\neq q\)，以及 \(N=pq, e, d>0\) 使得 \(\gcd(e,\Phi(N))=1\) 且 \(de=1\mod \Phi(N)\)
  算法允许在 negligible 的概率下失败：生成的 \(p,q\) 为合数 composite number

  
  对于 GenRSA 算法，RSA 问题是困难的当且仅当对于任意的 PPT 敌手 \(\mathscr{A}\)
  \(\Pr[\mathtt{RSAinv}_{\mathscr{A}, GenRSA}(n)=1]\leq \epsilon(n)\)
  RSA Assumption 是指，存在这样一个 GenRSA 算法，使得 RSA 是一个 hard problem; i.e., 给出 \(N,e\)，计算 uniform element \(y\in Z^*_N\) 的 \(e\) 次方根是困难的

  注意 GenRSA 算法与 GenModulus 算法的联系：GenRSA 可以通过 GenModulus 构筑：生成了 \(N,p,q\) 后，\(\Phi(N)=(p-1)(q-1)\)，\(e\) 及其模 \(\Phi(N)\) 意义下的逆元 \(d\) 也能通过 eGCD 算法找到

• RSA problem: difficulty
  这是 RSA 加密的安全性基础，也是将 RSA 与 Factoring 的困难性联系到一起的途径
  已知 \(N=pq,p\neq q\) 且 \(p,q\) 均为奇质数，那么 \(\Phi(N)=(p-1)(q-1)\)

  • 若 \(p,q\) 已知
    \(\Phi(N)\) 能被 efficiently 计算，因此 \(d=e^{-1} \mod \Phi(N)\) 也能被 efficiently 计算
    那么 \(y\) 在模 \(N\) 意义下的 \(e\) 次方根可以直接通过 \(y^{d} \mod N\) 计算出
    因此，在 \(p,q\) 已知的情况下，RSA 是一个 简单问题 (存在 efficient 的算法进行计算)
  • 若 \(p,q\) 未知
    计算 \(\Phi(N)\) 与 factoring \(N\) 一样困难 (可通过简单的归约说明)
    计算 \(d=e^{-1}\mod \Phi(N)\) 与 factoring \(N\) 一样困难
    因此，在 \(p,q\) 未知的情况下，RSA 的困难性与 factoring problem 的困难性一致

• One-Way Function
  单向函数 (one-way function) 是一个加密 primitive，在加密方案设计与 MAC 设计中都运用广泛
  informal 的定义是：One-way function is easy to compute but hard to inverse

  • \(\mathtt{Invert}\) 实验
    
  • One-Way Function 定义
    
  • 建立在 factory assumption 上的 One-Way Function
    
    
    (注意，这里的所有函数都是 deterministic 的，所以我们需要 random tape \(x\) 来生成 \(Gen\))
    

Back to Groups: Cyclic Groups 循环群

• 群元素 的阶 Order of a Group Element
  注意 Order 描述的对象：如果是群的阶 (Order of a Group)，那么指的是该群中元素的个数 \(|G|\)
  我们这里介绍的是群元素的阶 (Order of a Group Element)
  
  群元素 \(g\) 的阶指的是 \(g\) 生成 (generate) 的最小子群的阶 \(i\)
  
  根据费马定理的推论，若 \(g\in G\) 是一个阶为 \(i\) 的元素，那么对于任意 \(x\) 都有 \(g^{x}=g^{[x \mod i]}\)

• 循环群 Cyclic Groups
  若群 \(G\) 是循环群，则存在一个 \(g\in G\) 使得 \(<g>=G, (|<g>|=|G|=m)\)，且我们称 \(g\) 为该循环群的 generator 生成元
  
  若 \(G\) 的 generator 是 \(g\)，则对于任意 \(h\in G\)，都存在 \(x\in \{0,1,...,m-1\}\) 使得 \(g^{x}=h\)
  一些例子：
  
  注意到这里子集都是由 \(0\) 开始的：时刻记得 \(g^{0}=1\) 代表的是群的单位元 (indentity element)，\(\Z^{+}\) 是加法意义下的群，单位元为 \(0\)，所以在列举子集时由 \(0\) 开始
  由以上例子可以看出，对于循环群 \(G\)，并不是所有 \(g\in G\) 都是其生成元 generator

• Cyclic Group: Group of Prime Order 质数阶循环群
  
  (注意条件：除了单位元 identity element 之外的元素均是生成元 generator!)
  证明：
  首先我们要知道一个结论：the order \(i\) of any element \(g\in G\) divides the order \(m\) of the group (\(i|m\))
  根据费马定理的推论，由于 \(g^i=1\)，\(g^m=g^{[m\mod i]}=1\)
  可知 \(m\mod i\) 一定是 \(0,1,...i-1\) 之间的数；但 \(i\) 已经是满足 \(g^x=1\) 的最小正整数 \(x=i\) 了
  那么，满足 \(g^{x}=1\) 且 \(x=\in \{0,1,...,i-1\}\) 的 \(x\) 仅有 \(x=0\)
  所以 \(m\mod i=0\), \(i|m\)
  那么，当 \(m\) 为质数时，对于 \(g\in G\)，其阶 \(i\) 只有可能是 \(1\) 或者 \(m\) (\(i|m\))
  \(i=1\) 当且仅当 \(g=1\) (\(g\) 为单位元 identity element)，那么，除单位元之外的群元素 \(g\) 均满足 \(|<g>|=i=|G|=m\)

• Cyclic Groups: \(\Z^{*}_p\)
  
  注意，这一定理并不是前面质数阶循环群定理的推论，因为 \(|Z^{*}_p|=\Phi(p)=p-1\)，而 \(p-1\) 仅在 \(p=3\) 时是质数
  并且 \(\Z^*_p\) 的生成元个数一定等于 \(\Phi(p-1)\)
  见如下的证明 (引用自 OIwiki 原根)
  

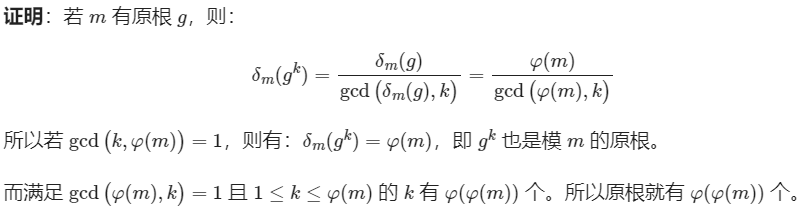
• Cyclic Groups：Uniform Sampling

Discrete-Logarithm Problem & Diffie-Hellman Problem

之前我们介绍了 Factoring 问题，以及建立在 Factoring 困难性上的模意义下开根问题 (RSA Problem)
这一节我们将会介绍模意义下取 \(\log\) 问题 (Discrete Logarithm Problem) 以及建立在其困难性上的 Diffie-Hellman Problem

• Discrete-Logarithm Problem 离散对数问题
  对于 \(q\) 阶的循环群 \(G\)，其生成元 generator 为 \(g\)
  所以有 \(G=\{g^0, g^1, ..., g^{q-1}\} (i=q)\)
  同样，对于任意 \(h\in G\)，一定存在 \(x \in \{0,1,...,q-1\}\)，使得 \(g^x=h\)
  我们定义 \(x=\log_g h\): \(x\) is the discrete logarithm of \(h\) with regard to \(g\)
  我们定义对循环群 \(G\) 的离散对数问题为：给出生成元 \(g\in G\) 与一任意选取的元素 \(h\)，计算 \(x=\log_g h\)
  
  

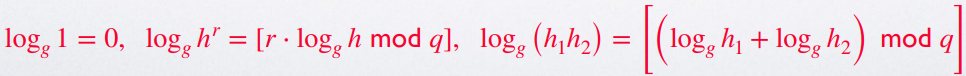
• Discrete-Logarithm Experiment
  
  注意，生成函数 \(\mathscr{G}\) 生成循环群 \(G\)，循环群的阶 \(q\) 与循环群的一个生成元 \(g\)
  

• Discrete-Logarithm Problem: Security
  
  Discrete-Logarithm Assumption 是指，存在这样一个群生成函数 \(\mathscr{G}\)，使得定义在其上的 Discrete-Logarithm Problem 是困难的
  回忆之前的两个 Assumptions：
  Factoring Assumption：存在函数 \(\mathtt{GenModulus}\) (生成 \(N, p, q\))，使得定义在其上的 Factoring Problem 是困难的
  RSA Assumption：存在函数 \(\mathtt{GenRSA}\) (生成 \(N, e, d\))，使得定义在其上的 RSA Problem 是困难的

• Diffie-Hellman Problem: Computational Diffie-Hellman (CDH)
  
  (这么定义的原因后面会提到，与 key exchange protocol 有关)
  显然，若对于 \(\mathscr{G}\) Discrete-Logarithm 是容易的，那么 CDH 问题也是容易的
  CDH 实验的定义 (观察与 Discrete Logarithm 实验定义的不同之处)

  1. Run \(\mathscr{G}\) to get \((G, q, g)\)
  2. Uniformly chosen \(x_1, x_2\) (这里是不同之处！如果取 \(h_1, h_2\)，那么连挑战者本人都无法判定敌手的回答是否正确)
  3. Compute \(h_1=g^{x_1}, h_2=g^{x_2}\) and sends to adversary

  之后的就差不多了(省略)，对于敌手输出的 \(Z\)，挑战者计算 \(g^{x_1\cdot x_2}\) 并进行比较检验
  基于该问题可以提出 CDH assumption

• Diffie-Hellman Problem: Decisional Diffie-Hellman (DDH)
  DDH 是 Diffie-Hellman Problem 的一个更强的定义 (相比 CDH 而言)，其对敌手的限制更少
  
  敌手并不需要真正计算出 \(h=DH_g(h_1, h_2)=g^{\log_g h_1\cdot \log_g h_2}\)，只需要分辨其与另一个随机的群元素 \(h'\)

• DDH Problem (Formal)
  
  
  这里虽然是一种 indistinguishable experiment，但是并不需要敌手输出 \(0/1\)
  挑战者将随机决定提供给敌手的是 \((g^{x_1}, g^{x_2}. g^{z}), z\in \Z_q\) 还是 \((g^{x_1}, g^{x_2}, g^{x_1\cdot x^2})\)

• Hardness of the Diffie-Hellman problems
  对于群生成函数 \(\mathscr{G}\)
  若离散对数问题简单 \(\to\) CDH 问题简单 \(\to\) DDH 问题简单
  也就是说，DDH assumption 最强，CDH assumption 其次，离散对数 assumption 最弱

Key-Exchange Protocols & DH Key-Exchange

感觉这个真的很妙啊！就算在公开的频道上交流，Alice 与 Bob 也能共同确立一个仅为他们所知的密钥
Key-Exchange 密钥交换也叫 Key-Establish，个人觉得后面这个名称更为准确，实际上就是双方共同确立一个密钥的过程

• Brief Intro: Key-Exchange Protocols

  • Parties (指 Bob 与 Alice 双方) holds \(1^{n}\)，运行 Probabilistic (Protocol 是随机的) Key-Exchange protocol \(\Pi\)，其交流基于在公频上传输的 transcript
  • 在运行 \(\Pi\) 之后，双方同时输出密钥 \(k_A=k_B=k\in \{0,1\}^n\)
  • 此时，Alice 与 Bob 可以用这个密钥 \(k\) 来建立一个安全的信道

  Security Goals：就算 attacker 在公开信道上观察到了 transcript，它也无法分辨密钥 \(k\) 与一个长度为 \(n\) 的随机串

• Key-Exchange Experiment
  

• Key-Exchange Security
  定义在 Key-Exchange Experiment 上的安全

  • Eavesdropper 存在的 Key-Exchange Protocol \(\Pi\) 是安全的，是指对于所有 PPT 敌手 \(\mathscr{A}\)，存在可忽略函数 \(\epsilon(n)\) 满足
    \(\Pr[KE^{eav}_{\mathscr{A}, \Pi}(n)=1]\leq \frac{1}{2}+\epsilon(n)\)

  对于 Key-Exchange Protocol 的 Security，还有更弱 (weak，指定义对敌手的限制更多) 的 computational notion (敌手获得 Transcript 后能够计算出密钥 \(k\))
  Indistinguishability 虽然是更强的定义，但不可分辨安全已经能够保证密钥 \(k\) 应用在接下来的单钥加密方案中的安全性

• Diffie-Hellman Key Exchange Protocol
  现在我们能够知道为什么建立在离散对数困难性上的 DH 问题要那样定义了：它就是为了 Key-Exchange 而准备的
  
  敌手能够观察到的 transcript 包括 \(G,q,g,h_A,h_B\)，不包括 Alice 与 Bob 随机选择的 \(x\) 与 \(y\)
  这是理论上 DH Key-Exchange Protocol 的定义
  实际运用中，\((G,q,g)\) 并不是由 \(\mathscr{G}\) 生成，而是标准化的，固定的，同时被 Alice 与 Bob 双方所知的
  因此，Alice 仅需要发送 \(h_A\) 给 Bob，而 Bob 也不需要等到收到 \(h_A\) 后再发送 \(h_B\)

  实际上，OTP 也可视作广义的 DH 密钥交换协议：在 OTP 中，\(G\) 是所有定义在位异或运算上的 \(n\) 位比特串 (bit strings under bit-wise XOR)

• Security of Diffie-Hellman Key Exchange
  安全性的依赖性：DH Key Exchange \(\to\) Hardness of DDH/CDH Problem \(\to\) Hardness of Discrete Logarithm
  在敌手观察到 \(G, q, g, g^{x}, g^{y}\) 的情境下，敌方想要获取的目标密钥是 \(k=g^{xy}\)
  通过 transcript 计算 \(k=g^{xy}\) 本质上就是 CDH 问题，分辨 \(g^{xy}\) 与一个随机群元素本质上就是 DDH 问题
  因此，若存在 \(\mathscr{G}\) 使得 DDH 问题困难，则该 key-exchange protocol 是安全的 (在下面给出 formal proof)

• Diffie-Hellman Key-Exchange Protocol: Security
  
  证明：PPT 敌手 \(\mathscr{A}\) 参与实验。根据定义，有 \(\Pr[b=0]=\Pr[b=1]=\frac{1}{2}\)
  则根据全概率公式有 \(\Pr[\widehat{KE}^{eav}_{\mathscr{A}, \Pi}(n)=1]=\frac{1}{2} \cdot \Pr[\widehat{KE}^{eav}_{\mathscr{A}, \Pi}(n)=1|b=0]+\frac{1}{2}\cdot \Pr[\widehat{KE}^{eav}_{\mathscr{A}, \Pi}(n)=1|b=1]\)
  在该实验中，敌手获得的 transcript 包含 \((G, q, g, h_1, h_2, k')\)
  \(b=0\) 时有 \(k'=k\)，\(b=1\) 时 \(k'\) 是一个随机的群元素：分辨这两者恰好就是 Decisional Diffie-Hellman 问题

\[\begin{aligned} \Pr[\widehat{KE}^{eav}_{\mathscr{A}, \Pi}] &= \frac{1}{2} \cdot \Pr[\widehat{KE}^{eav}_{\mathscr{A}, \Pi}(n)=1|b=0]+\frac{1}{2}\cdot \Pr[\widehat{KE}^{eav}_{\mathscr{A}, \Pi}(n)=1|b=1]\\ & = \frac{1}{2} \Pr[\mathscr{A}(G, q, g, g^{x}, g^{y}, g^{xy})=0]+\frac{1}{2} \Pr[\mathscr{A}(G, q, g, g^{x}, g^{y}, g^{z})=1] \\ & = \frac{1}{2} (1-\Pr[\mathscr{A}(G, q, g, g^{x}, g^{y}, g^{xy})=1]+\Pr[\mathscr{A}(G, q, g, g^{x}, g^{y}, g^{z})=1]) \\ & = \frac{1}{2} + \frac{1}{2}(\Pr[\mathscr{A}(G, q, g, g^{x}, g^{y}, g^{z})=1]-\Pr[\mathscr{A}(G, q, g, g^{x}, g^{y}, g^{xy})=1]) \\ & \leq \frac{1}{2} + \frac{1}{2} |\Pr[\mathscr{A}(G, q, g, g^{x}, g^{y}, g^{z})=1]-\Pr[\mathscr{A}(G, q, g, g^{x}, g^{y}, g^{xy})=1]| \end{aligned} \]

注意，这里的概率建立在 \(\mathscr{G}(1^n)\) 生成的 \((G, q, g)\)，以及随机选取的 \(x\), \(y\), \(z\) 上
\(g\) 是群 \(G\) 的一个生成元且 \(z\in \Z_q\)，因此 \(g^z\) 是一个 \(G\) 中一个随机的群元素
因此，若 \(\mathscr{G}\) 使得 DDH 是困难的，则对于任何 PPT 敌手都有 \(\mathscr{A}\) 有 \(|\Pr[\mathscr{A}(G, q, g, g^{x}, g^{y}, g^{z})=1]-\Pr[\mathscr{A}(G, q, g, g^{x}, g^{y}, g^{xy})=1]| \leq \epsilon(n)\)
则 \(\Pr[\widehat{KE}^{eav}_{\mathscr{A}, \Pi}]\leq \frac{1}{2} + \frac{1}{2} |\Pr[\mathscr{A}(G, q, g, g^{x}, g^{y}, g^{z})=1]-\Pr[\mathscr{A}(G, q, g, g^{x}, g^{y}, g^{xy})=1]|\leq \frac{1}{2}+\frac{1}{2}\epsilon(n)\)
若存在 \(\mathscr{G}\) 使得 DDH 是困难的，那么 Diffie-Hellman Key-Exchange Protocol \(\Pi\) 是安全的

• Key Derivation
  通过 DH key-exchange protocol 得到的密钥 \(k\) 是某个群 \(G\) 中的一个元素 \(k=g^{xy}\)
  而该元素 \(k\) 的长度不一定为 \(n\)，甚至不一定是个均匀串 uniform string
  而大多数时候我们在加密方案中使用的密钥长度需要等于 security parameter \(1^{n}\)
  为了确保这一点，我们采用 Key Derivation: 获得 \(k'=H(k)\)，其中 \(H\) 是一个合适的哈希函数，输出一个长度为 \(n\) 的哈希值
  (proper 是指，其具有 stronger properties 例如 collision-resistance；重要是能够保证输出 \(H(k)\) 接近随机 random)

• Authenticated Key-Exchange
  我们之前介绍的 DH Key-Exchange protocol 在面对窃听者 (eavesdropper) 时是安全的
  然而 Eavesdropper 采取的攻击是被动的 (passive attacks)，对于主动攻击 (active attacks)，DH 密钥交换协议是不安全的
  例如：

  • Impersonation attacks：敌手冒充一方与另一方进行交互
  • Man-in-the-middle attacks：中间人攻击，敌手在 \(A,B\) 双方之间占据 \(C\)，对 \(A\) 冒充 \(B\)，对 \(B\) 冒充 \(A\)，从而实现对信息以及密钥的全面掌握

  能够防范主动攻击的密钥交换协议是 Authenticated Key-Exchange Protocol，这意味着双方对能够辨识信源的身份 (identity)，且知道共享密钥的人的身份
  现代大多数的密钥交换协议提供 Authenticated Key-Exchange，例如传输层安全 Transport Layer Security

Public Key Encryption 公钥加密 —— El Gamel Encryption

• Asymmetric Cryptography 非对称加密
  之前提到过私钥加密的另一个名称：对称加密，现在我们终于可以知道 对称 (symmetric) 这一词在加密学中的含义了
  在公钥加密中

  • Receiver Alice 生成一对 \((pk,sk)\)，其中 \(pk\) 是公钥，\(sk\) 是私钥
  • 公钥 \(pk\) is widely disseminated，可被 任何 sender 所使用; 而私钥 \(sk\) is kept secret，Alice 解密时将会用到私钥
  • receiver 与 sender 双方并不会 share 共同的密钥 (因此，之前的 密钥交换协议 key-exchange protocol 当属私钥加密范畴，因为密钥交换的过程相当于设立了双方共同的密钥 (prior secret key))

  可以看出，receiver 和 sender 双方持有的密钥是不对称的：只有 receiver 拥有私钥 \(sk\)
  因此公钥加密也被称为 非对称加密 Asymmetric Encryption

• Public Key Encryption
  
  几点注意：

  • 公钥与私钥并不一定是完全无关的，不如说，大部分公钥加密中的公钥与私钥都存在一定程度上的联系
  • 非对称性 (asymmetric) 同样体现在加密与解密的过程中：加密使用公钥 \(pk\)，而解密使用私钥 \(sk\)
  • 若公钥是由 receiver 传送给 sender 的，则要求传输的信道必须是 authenticated 的；否则敌手可以轻松的截获并修改传输的公钥，从而实现 impersonation 攻击或中间人攻击；(若公钥被 receiver 公布在某个能验证身份的 online repository 或是 website 上，这就保证了 authenticated)

  正确性：对于一对 \((pk, sk)\)，对于任意 legal message \(m\)，都有 \(Dec_{sk}(Enc_{pk}(m))=m\)
  

• Eavesdropping Indistinguishability Experiment \(\mathtt{PubK}^{\mathtt{eav}}_{\mathscr{A}, \Pi}\)
  
  注意：敌手拥有公钥 \(pk\)，且能够在已知该公钥的知识基础上选择输出 \(m_0,m_1\)

• Computational (EAV) Security in the Public Key Setting
  
  (不可分辨实验的标准定义：概率 \(\leq 1/2+\varepsilon(n)\))

• CPA Security in the Public Key setting

  • 先贴出结论：公钥加密背景下的 EAV secure 与 CPA secure 等价
    
    EAV secure 的定义：敌手仅有 窃听 (EAVesdropping) 权限，在该定义下加密方法安全
    CPA secure 的定义：敌手有 窃听与加密 权限，在该定义下加密方法安全
    而在公钥加密中，EAV 敌手不仅能够窃听到密文 \(c\)，还能窃听到 公钥 \(pk\) —— 而拥有公钥则意味着拥有 Encryption Oracle \(Enc(\cdot)\)
    因此，在公钥加密背景下，EAV secure (能通过 EAV indistinguishability 实验) 等价于 CPA secure
  • 与私钥加密类似，所有 deterministic 的公钥加密方法一定不是 CPA secure 的 (敌手可以简单的将 \(m_0,m_1\) 加密再与挑战密文比对即可在不可分辨实验中获胜)

• Public Key Encryption CANNOT be perfectly secure
  私钥加密中，OTP (一次性密码本) 是完美安全的；
  然而，对于公钥加密，不存在一种公钥加密方法是完美安全的
  

  若公钥加密方法 \(\Pi\) 是完美安全的，那么对于任意拥有 unbounded computational power 的敌手 \(\mathscr{A}\) 都有
  
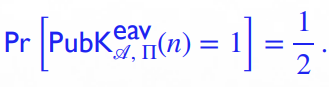
  而事实上，对于拥有无限计算能力的敌手，这个概率是 \(1\) (百分百能够在实验中获胜)

  拥有无限计算能力的敌手 \(\mathscr{A}\) 掌握公钥 \(pk\)，且输出了 \(m_0,m_1\)，其如何判断挑战密文 \(c_b\) 是由哪一条明文加密而来的呢？
  答案很简单：通过 Brute-force，得到 \(m_0\) 所有可能的密文集合 \(\{c_0\}\)，若 \(c_b\in\{c_0\}\) 输出 \(0\)，否则输出 \(1\)
  (例：若公钥加密采用 \(r=\{0,1\}^n\) 作为随机因子，则敌手取所有可能的 \(r\) 对来计算密文集合 \(\{c_0\}\): \(c_r:=Enc_{pk}(0;r)\) for all \(r\in\{0,1\}^n\))

• Multiple messages security
  
  与私钥加密相同：单条信息安全代表多条信息安全
  

• CCA indistinguishability experiment in public key setting
  对于公钥加密，最需要防范的攻击之一就是 CCA 攻击：这是因为，攻击者可以完全 伪装成正常的用户 (legitimate sender) 对 receiver 进行 CCA 攻击
  以下是一个可能的 CCA 攻击过程：

  • 攻击者获取了一封加密的邮件 \(c'\)
  • 攻击者伪装成正常用户，将该加密的邮件发送给 Alice
  • 若 Alice 回复给攻击者的邮件中包含对原邮件的直接引用 quotation \(m'\)，则敌手可以获取到对应的 \((c', m')\) 对

  公钥加密的 CCA 不可分辨实验如下：
  

• public key：CCA security
  
  这一部分与私钥加密的定义一模一样，包括 multiple messages CCA security，malleability 性质等
  (再次回顾 malleability 的定义：对于原文是 \(m\) 的密文 \(c\)，敌手能够生成 \(c'\)，令 \(m\) 与 \(m':=Dec(c')\) 之间有某种可预测的关联)
  任意 malleable 的公钥加密方法一定不是 CCA-secure 的

• El Gamel Encryption Scheme
  之前我们介绍了基于 Diffie-Hellman problem 的密钥交换协议： Diffie-Hellman Key-Exchange Protocol
  接下来将介绍同样基于 Diffie-Hellman problem 的公钥加密法：El Gamel Encryption Scheme
  

  • El Gamel 的随机性依赖于 sender 选择的 \(y\): 对于同一条消息 \(m\)，多次加密，由于选择的 \(y\) 不同，密文也不同 (注意，敌手不能获取 \(y\))
  • El Gamel 加密法的公钥与密钥之间的关系：\(pk=g^{sk}\)
  • 正确性：\(\widehat{m}=c_2/c_1^x=(h^y\cdot m)/(g^y)^x=(g^x)^y\cdot m/g^{xy}=m\)
  • 注意：明文空间 \(\mathscr{M}=G\)，也就是说，legal \(m\in G\)

• El Gamel Encryption: CPA security
  
  很标准的 proof of reduction，详细见 Lec 17 slides-Security of El Gamal encryption scheme: Analysis
  同样，需要证明的命题的敌手作为已经证明的命题的敌手的 subroutine:
  外层 \(D\): DDH 问题的 distinguisher，given \(h_1=g^x, h_2=g^y, h_3\)，分辨 \(g^3=g^{xy}\) 还是一个随机的群元素 \(g^z\)
  内层 \(\mathscr{A}\): El Gamel 加密的敌手，进行实验 \(\mathtt{PubK}^{\mathtt{eav}}_{\mathscr{A}, \Pi}\)，其中 \(\Pi\) 是 El Gamel 加密
  构建好 reduction 之后根据常规进行证明

• Hybrid Encryption
  对于 El Gamel 加密法，我们有要求 \(m\in G\) (这个条件大部分情况下都能满足)
  然而，对于不满足条件的 \(m\)，我们这样处理：
  
  混合加密：选择 \(k\in G\) 并用 El Gamel 进行加密，再用某个 key-derivation 函数 \(H\) 进行调整 (\(H\) 的存在使得 \(m\) 可以任意长)，最后使用 \(k'=H(k)\) 作为密钥加密 \(m\) (采用合适的私钥加密法)

• El Gamel Encryption: NOT CCA secure
  El Gamel Encryption 不是 CCA 安全的，因为它是 malleable 的
  对于某条 El Gamel 加密的密文 \(c=(c_1, c_2)\) (\(c_1=g^y, c_2=g^{xy}\cdot m\))，敌手对其进行修改 \(c'=(c_1, 2c_2)\)
  那么，解密后的消息 \(m'=2m\)
  对密文的修改引起了可预测的变化 \(\to\) El Gamel 加密是 malleable 的 \(\to\) El Gamel 加密不是 CCA 安全的

RSA Encryption

接下来，我们将介绍第二个公钥加密方法 : RSA Encryption
第一个公钥加密方法是 El Gamel Encryption: 其安全性基于 Diffie-Hellman Assumption，又基于 Discrete Logarithm
而 RSA Encryption 安全性基于 RSA Assumption (e-th root modulo \(N\))，又基于 Factoring Problem

• Plain/Textbook RSA Encryption Scheme
  
  注意，在某些实现中，我们使用 \(de=1\pmod{LCM(p-1, q-1)}\) 而不是 \(de=1\pmod{\varphi(N)}\)

• Plain RSA Encryption: uniform \(m\)
  注意 RSA Assumption 的定义: 模 \(N\) 意义下计算 \(c\) 的 e-th root 是困难的当且仅当 \(c\) 是 uniform 的 (\(c\) is uniformly chosen from \(\Z_N^*\))
  而由于 \(c=[m^e\mod{N}]\)，\(c\) 是 uniform 意味着 \(m\) 是 uniform 的
  因此，Plain RSA Encryption 的安全性 implicitly 依赖信息 \(m\) 的随机性: \(m\) must be uniformly chosen from \(\Z^*_N\)，否则 Plain RSA Encryption 不是安全的

• Plain RSA Encryption: \(m\) is only "entirely" secure
  注意 RSA Assumption 只保证计算 uniform \(c\) 的完整 e-th root 的困难性
  这意味着，想要得到完整的 \(m \ (m^e=c)\) 是困难的，然而这并不保证得到 \(m\) 的一部分是困难的
  事实上，即使 \(c\) 是 uniform 的，其 e-th root 的 partial information 仍然有可能泄露 (有方法能计算 \(m\) 的特定 bits)

• Plain RSA Encryption: NOT very secure
  即使 \(m\) 是 uniform 的并且泄露 \(m\) 的几个 bits 是可接受的，针对 Plain RSA Encryption 的攻击还有很多 (e.g. Hastad's broadcast attack, meet-in-the-middle attack)

  • 并且 Plain RSA Encryption 不是 CPA-secure 的:
    Plain RSA Encryption 是 deterministic 的，因此其一定不是 CPA-secure 的 (Plain RSA Encryption 无法通过 \(\mathtt{PubK}^{\mathtt{eav}}_{Plain \ RSA}\) 不可分辨实验)
  • Plain RSA Encryption 不是 CCA-secure 的
    虽然不是 CPA-secure 的加密方法也同样一定不是 CCA-secure 的，我们还是采用说明 Plain RSA Encryption 是 malleable 来证明岂不是 CCA-secure
    对于 \(c=m^e\mod{N}\)，我们有 \(Dec(c)=m\)
    对 \(c\) 进行修改 \(c'=[2^ec\mod{N}]=[(2m)^e\mod{N}]\)，因此 \(Dec(c')=2m\)
    这样，我们对 \(c\) 进行修改，对应的 \(m\) 将发生可预测的改变，所以 Plain RSA 是 malleable 的，所以其不是 CCA-secure 的

• Attacks on Plain RSA: e-th root attack
  RSA assumption 指出了模 \(N\) 意义下求 uniform \(c\in\Z^*_N\) 的 e-th root 的困难性
  但是，对于某个 integers 求 e-th root 并不困难，存在对应的 efficient 的算法
  这样，对于 \(e\) 较小的 Plain RSA，我们能对某个较小的 \(m\) 实施 e-th root attack
  
  由于 \(m\) 与 \(e\) 都很小，\(m^e<N\)，所以并不会涉及到模 \(N\) 意义下的求 \(e\) 次根，只需要对一个整数 \(c\) 求 \(e\) 次根；而这一操作是可以在 \(poly(||c||)=poly(||N||)\) 时间内完成
  

• Attacks on Plain RSA (for longer messages): Coppersmith
  首先介绍 Coppersmith'theorm
  
  Coppersmith 设计了一种算法，可以 efficiently 的求出多项式的小根 (small roots)：对于 \(e\) 阶多项式 \(p(x)\)，Coppersmith 算法能在模 \(N\) 意义下快速求出 \(p(x)\) 所有小于 \(N^{1/e}\) 的根
  这个算法能够对 Plain RSA 进行高位已知攻击:
  
  
  既然 \(c=[(m_1||m_2)^e\mod{N}]=[(2^l\cdot m_1+m_2)^e\mod{N}]\)，且 \(c, e,N,m_1,l\) 已知
  我们令 \(p(x)=(2^l\cdot m_1+x)^e-c \pmod{N}\)，对于 \(e\) 阶的多项式 \(p(x)\)，若 \(x=m_2\leq N^{1/e}\)，我们应用 Coppersmith 算法能够快速求出所有可能的 \(x\) 使得 \(p(x)=0\)
  这样，在已知信息高位 \(m_1\) 的情况下，\(m_2\) 就被破解了 (构造了 \(p(x)\) 使得 \(m_2\) 作为 \(p(x)\) 的根)
  注意，若我们不知道信息的高位，直接对 Plain RSA 实施 coppersmith 攻击，那么这样的攻击与 e-th root 攻击是等价的 (由于 Coppersmith 算法要求 \(m< N^{1/e}\), 即 \(m^e<N\)，我们只需要进行整数求 \(e\) 次根即可)

• Attacks on Plain RSA (for related messages): Franklin-Reiter
  
  敌手观察到两条密文 \(c_1=[m^e\mod{N}], c_2=[(m+j)^3\mod{N}]\)
  因此，对于两个 \(e\) 阶多项式 \(f_1(x)=x^e-c_1\mod{N}\), \(f_2(x)=(x+j)^e-c_2\mod{N}\)，可以发现 \(x=m\) 同时是 \(f_1, f_2\) 的根
  因此 \((x-m)\) 同时是 \(f_1, f_2\) 的 factor，同样也会是 \(\gcd(f_1, f_2)\) 的 factor (或甚至就是 \(\gcd\) 本身)
  若通过 Franklin-Reiter 算法计算出的 \(\gcd(f_1, f_2)\) 是 \(x-r\) 的形式，则 \(m=r\)
  

• Padded RSA Encryption
  Padded RSA Encryption 将向 Plain RSA 中添加随机性 (即，添加 random pad)，使其具有 CPA-secure
  
  
  注意：

  • Padded 过后的 message \(\hat{m}=r||m\) 必须满足 \(\hat{m}<N\) 并且 \(\hat{m}\in \Z^*_N\): 这是因为，如果 \(\hat{m}>N\)，那么进行 Decrypt 时我们得到的将是 \([\hat{m}\mod N]\) 而不是 \(\hat{m}\) 本身，这将带来很多不必要的麻烦。为了达到这个要求，我们使用一个合适的 \(l\) 来规定 \(r\)，使得 \(r||m<N\)
  • we prepend \(r\) instead of appending \(r\) to \(m\)，若 \(\hat{m}=m||r\)，则 \(c=(m||r)^e\). 在这种情况下，敌手可以通过 \(c/2^{le}=(m||r)^e/2^{le}=((m||r)/2^l)^e=m^e\) 来消除 pad \(r\) 带来的随机性，因此是不安全的

• Padded RSA Encryption: Security
  
  
  
  可以看出 Padded RSA Encryption 的 security 依赖于 \(l\): 随着 \(l\) 的改变，Padded RSA Encryption 的改变可视作一个 continuum

• Padded RSA Encryption: Definition
  
  注意 \(m\) 的长度 \(|m|=||N||-l(n)-2\)

• Exercise
  复习时记得看看 Lec 18 Slides 的两个 Exercise
  一个在开头，一个在末尾

Hard-Core Predicates 硬核谓词

• the idea of Hard-Core Predicates
  对于某个 one-way function \(f\)，不存在任何 PPT 敌手由 \(y=f(x)\) 计算出其原像 (preimage value) \(x\)
  然而，即使 \(f\) 是单向函数，\(y=f(x)\) 仍然有可能泄露关于 \(x\) 的信息
  
  Hard-Core Predicates \(hc\) 就是这样一种函数：对于某个单向函数 \(f\), \(hc(x)\) 代表若敌手拥有 \(y=f(x)\) 也不会遭到泄露的信息
  

• Hard-Core Predicates: Definition
  
  给出 \(x\)，其硬核谓词 \(hc(x)\) 能在 PPT 时间内计算出
  然而 PPT 敌手在 given \(f(x)\) 的情况下也无法以不可忽略的优势得到 \(hc(x)\)

• A Hard-Core Predicate for the RSA problem: lsb(x)
  lsb() 是 RSA 问题的一个硬核谓词: 通俗来讲，就是敌手给定 \(c=m^e\mod{N}\)，也无法以不可忽略的优势确定 \(lsb(m)\)
  (而给定 \(x\), \(lsb(x)\) 能被 efficiently 计算)，由此可见硬核谓词 \(hc()\) 是对单向函数定义的一个 放松 (relax)，或是说，更强的定义
  这也是所谓的：有硬核谓词的函数 \(f\) 一定是单向函数，没有硬核谓词的函数 \(f\) 也不一定不是单向函数

  RSA 硬核谓词实验:
  

• (重要!!) A Hard-Core Predicate for the RSA Problem: lsb(x) (Proof)
  
  (概率有 \(1/2\) 是因为敌手可以输出一个 random guess)
  证明还是老样子，proof of reduction，我们将计算 \(hc(x)\) 的困难性归约到计算原像 \(x\) 的困难性上: 即，若存在 \(\mathscr{A}\) 能够在得知 \(f(x)\) 的前提下 efficiently 计算 \(hc(x)\)，那么他也能够还原整个 \(x\)
  
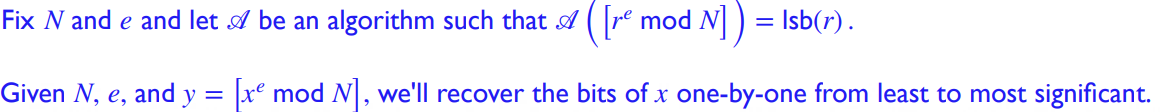
  首先, 运行 \(\mathscr{A}(y)\) 得到 \(lsb(x)\). 考虑下面两种情况：

  • \(lsb(x)=0\)
    若 \(lsb(x)=0\), \(x=2k\). 我们可以得到 \(f(x/2)\equiv (x/2)^e\equiv x^e/2^e\equiv f(x)/2^e\pmod{N}\)
    当 \(2|x\) 时，\(x/2\) 与 \(x>>1\) 等价，因此得到 \(f(x/2)\) 意味着得到 \(f(x>>1)\)，敌手从而能够计算 \(lsb(x>>1)\) 即 \(2sb(x)\)
  • \(lsb(x)=1\)
    若 \(lsb(x)=1\), \(x=2k+1\)
    首先观察到这样一个事实 \([x/2\mod N]=(x+N)/2\)
    所以 \(lsb([x/2\mod N])=lsb[(x+N)/2]=2sb(x+N)=2sb(x)\oplus 2sb(N) \oplus 1\) (注意，由于 \(x\) 与 \(N\) 均为奇数，\(2sb\) 需要接受 \(lsb\) 的 进位 carry bit \(1\))
    计算 \(y'\equiv [y/2^e\mod N]\equiv f(x/2)\pmod{N}\)，运行 \(\mathscr{A}(y')\) 得到 \(lsb([x/2\mod{N}])\) (注意，这里的 \(x/2\) 不再代表 \(x>>1\))
    敌手能够计算 \(2sb(x)=\mathscr{A}(y')\oplus 1\oplus 2sb(N)\)

  这样，敌手能 bit-by-bit 的从 \(lsb\) 到 \(msb\) 还原出整条消息 \(x\)，从而证明能够由 \(y=f(x)\) efficiently 计算 \(hc(x)\) 的敌手同样能够还原原像 \(x\)

• Single-bit Encryption using the Hard-core Predicate for RSA
  现在，我们知道了 RSA 问题的硬核谓词是密文的 \(lsb\)，我们可以利用它来设计一个对 单比特 的加密方案
  
  很明显，如果 GenRSA 能够使得 RSA 问题是困难的，则该加密方案是安全的 (因为敌手无法以不可忽略的优势计算出 \(lsb(r)\)，也就无法得到单比特密文)

• Security of Single-Bit Encryption
  
  证明见 Lec 19，还是很经典的 proof of reduction
  归约机的构造: \(\mathscr{S}\) 得到 \(y=[x^3\mod N]\) 后尝试求 \(lsb(x)\)，其将 \(y\) 作为挑战密文传给 \(\mathscr{A}\): 设 \(\mathscr{A}\) 输出的结果为 \(b'\)，则 \(lsb(x)=b'\)
  另外需要注意的一点: 由于随机化 \(r\) 的存在 (更精确的说是 \(r[1...n-1]\))，该加密方案是 CPA-secure 的

Digital Signatures 数字签名

数字签名的公-私钥关系与公钥加密相反
在公钥加密中，sender 用公钥 \(pk\) 加密消息 \(m\), receiver 用私钥 \(sk\) 解密密文 \(c\)
而在数字签名中，sender 用私钥 \(sk\) 认证消息 \(m\)，receiver 用公钥 \(pk\) 证实签名 \(\sigma\)
与 MAC 相比，数字签名简化了密钥的 distribution and management
当 sender 想要向多个 receiver 传送 authenticated 的信息时尤其如此
数字签名的安全目标 (security goal): 即使敌手能够观察到 Alice 对多条信息的签名，针对一个新的信息 \(m\)，其也无法 forge 出一个 valid 的签名

Digital Signature Scheme

在数字签名 Assumption 中，receiver 能够 legitimate 的获取 sender 提供的公钥 \(pk\)，说明 sender is able to transmit at least one message, i.e., \(pk\) in a reliable and authenticated manner.
注意 at least one，若 \(pk\) 被安全的传输，则数字签名能够开始使用

Security of Digital Signature Scheme: Digital Signature Experiment

使用数字签名实验来定义数字签名的安全性
Threat Model: PPT 敌手拥有 \(Sign\) 的 oracle access，这意味着其能够执行 "Adaptive Chosen-Message Attack"
Security Goal: 与 MAC 相同，即 Existential Unforgeability


Points to Note:

• 注意具体的定义：对于某个新的 \(m\)，敌手无法 forge 出其的签名 \(\sigma\) ( 我们强调敌手必须对给定的 \(m\) 进行 forge，是因为在某些情况下，敌手能够伪造出 valid 的 \((m, \sigma)\) 对 )
• 由于该实验不是 distinguishability 实验而是 forge 实验，与 MAC 类似，其最终的概率是 \(\varepsilon(n)\) 而不是 \(1/2+\varepsilon(n)\)

Digital Signature V.S. Message Authentication Code (MAC)

1. Public Verifiability
   若某个 receiver 验证对 \(m\) 的签名 \(\sigma\) 是合法的，那么所有 receivers 对该 \((m, \sigma)\) 对的验证都将是合法的
   (若使用 MAC 进行 authenticate，那么当 \(k\) 一致时也能实现 Public Verifiability；然而 \(k\) 一致时一个恶意的 receiver 将能获取到 \(k\)，并成功 forge 出 MAC )

2. Transferability
   对 \(m\) 的签名 \(\sigma\) 能被第三方进行验证，只要使用 sender 的公钥 \(pk\) 即可
   (对 MAC 则不行，若第三方想要验证 \(m\) 的 MAC \(t\)，其需要得知密钥 \(k\)；而密钥 \(k\) 的权威性并未得到 sender 的 authenticate，其又可能是 receiver 假冒生成的)

3. Non-Repudiation (不可否认性)
   若 sender 的公钥 \(pk\) 是 widely publicized and distributed 的，且其私钥 \(sk\) 并未泄露，则只要 sender 签署了某条信息 \(m\)，之后其就不能否认这件事
   Non-repudiation 的基础在于 transferability
   (MAC 则完全无法提供 non-repuditation; 若要判断 tag 是否是由 sender 产生，就要获取密钥 \(k\) 由第三方进行验证; 而提供 \(k\) 的 receiver 也完全无法证明密钥的 authentication。相反，数字签名中的公钥 \(pk\) 是广为人知的，具有公信力)

The Hash-and-sign Paradigm

数字签名的效率整体上来说要低于 MAC
回想我们接触的公钥加密 RSA, 或者 Diffie-Hellman，都存在大量的指数运算 (\(c=m^e, m=c^d; c=g^{x_1x_2}...\))
因此，为了提高效率，一般采用 Hash 先将信息压缩成较短的 digest，再进行数字签名 sign
这种方式被称作 Hash-and-Sign

这与 Hash-and-MAC 的原理很相似

Hash-and-sign Digital Signature Scheme

Hash-and-sign Digital Signature: Security

可以说与 Hash-and-MAC 的安全证明过程完全一致
敌手 \(\mathscr{A}'\) 进行数字签名 forge 实验 \(\mathtt{SigForge}_{\mathscr{A'}, \Pi'}(n)\)
其中，公钥为 \((pk, s)\), 私钥为 \((sk, s)\)
若敌手成功 forge 出 \((m^*, \sigma), \ m^*\notin Q\)
我们考虑以下两种情况

• \(H^s(m^*)=H^s(m)\)，其中 \(m\in Q\)
  这种情况下，哈希冲突发生，我们将其 denote 为 \(\mathtt{coll}\)
• \(H^s(m^*)\neq H^s(m)\) for all \(m\in Q\)

敌手赢得 \(\mathtt{SigForge}\) 实验的概率是
\(\Pr[\mathtt{SigForge}_{\mathscr{A'}, \Pi'}(n)=1]=\Pr[\mathtt{SigForge}_{\mathscr{A'}, \Pi'}(n)=1 \and \mathtt{coll}]+\Pr[\mathtt{SigForge}_{\mathscr{A'}, \Pi'}(n)=1\and \overline{\mathtt{coll}}]\leq \Pr[\mathtt{coll}]+\Pr[\mathtt{SigForge}_{\mathscr{A'}, \Pi'}(n)=1\and \overline{\mathtt{coll}}]\)
我们将证明该概率是 negligible 的: 其中第一项用 Hash collision-resistance 证明，第二项用 \(\Pi\) 的 unforgeability 证明

• \(\mathtt{coll}\) 发生
  构建 reduction: 利用 \(\Pi'\) 的敌手 \(\mathscr{A}'\) 来构建 \(H\) 的敌手 \(C\) (来找到 \(H\) 的一对 collision)
  省略具体构建过程，最后我们得到 \(\Pr[\mathtt{coll}]=\Pr[\mathtt{Hash}^{\mathtt{coll}}_{\mathscr{A}, H}(n)=1]\leq\varepsilon_1(n)\) for negligible \(\varepsilon_1(n)\)

• \(\mathtt{coll}\) 未发生
  构建 reduction：利用 \(\Pi'\) 的敌手 \(\mathscr{A}'\) 来构建 \(\Pi\) 的敌手 \(\mathscr{A}\)
  \(\mathscr{A}\) 有 \(\Pi\) 的 signing oracle，对于任意 \(m\) 可以获得对应的 \(sign(m)\)

  • \(\mathscr{A}\) 运行 \(Gen_H(1^n)\) 得到哈希函数的 \(s\)
  • 运行 \(\mathscr{A'}(1^n)\)，对于 \(\mathscr{A}'\) 的询问 \(m_i\in\{0,1\}^*\)，\(\mathscr{A}\) 计算 \(H^s(m_i)\) 并询问 signing oracle 得到 \(sign(H^s(m))\)，回复给 \(\mathscr{A}\)
  • \(\mathscr{A}'\) 输出 \((m^*, \sigma)\)
  • \(\mathscr{A}\) 输出 \((H^s(m^*), \sigma)\)

  由此，得到 \(\Pr[\mathtt{Sig}^{forge}_{\mathscr{A}', \Pi'}(n)=1\and\overline{\mathtt{coll}}]=\Pr[\mathtt{Sig}^{forge}_{\mathscr{A}, Pi}(n)=1]\leq \varepsilon_2(n)\)

最终，证明 \(\Pr[\mathtt{SigForge}_{\mathscr{A}', \Pi}(n)=1]\leq\epsilon_1(n)+\epsilon_2(n)=\epsilon(n)\)，所以任何由 collision-resistant 的哈希函数 \(H\) 与任何 Existentially unforgeable 的数字签名 scheme \(\Pi\) 组成的 Hash-and-Sign 数字签名 \(\Pi'\) 是安全的

Textbook RSA Digital Signature Scheme

注意 Digital Signature 的 Verify 函数与 MAC 中的 Verify 函数的区别
在 MAC 中，verify 一个 tag 的方式是计算 \(MAC(m)\) 并将其与 tag 比较：这样做的安全性基于密钥 \(k\) 的安全性
而在 Digital Signature 中，verify 一个 signature 的方式是根据公钥 \(pk\) 与 签名 \(\sigma\) 计算 \(m'\) 并与 \(m\) 比较 (更类似于加密过程？但签名并不保证 confidentiality)

(In)security of the Plain RSA

按照惯性思维，我们可能认为以 RSA 构筑的数字签名是安全的：因为敌手必须知道 \(e\) 才能 sign 某个消息 \(m\)
但是由于敌手掌握 signing oracle (敌手掌握 signing oracle 的行为并不受 RSA assumption 保证)，该数字签名方案有许多种攻击方案

• Attack on RSA assumption
  首先，RSA assumption 中的敌手并不能获得 \(m\) 所对应的 \(m^d\)，而 Digital Signature 中的敌手拥有 signing oracle
  而且一定要记住 RSA assumption 中的前提条件，对于 uniform \(m\)，由 \(m^d\) 计算 \(m\) 是困难的：而在 Digital Signature 中，无法保证 \(m\) 的随机性

• No query message attack (敌手不使用 signing oracle)
  首先，一个显而易见的攻击是 \(m=1\): 敌手一定能 forge \((m=1,\sigma=1)\)
  另外，敌手一定能 forge 随机的 \(m\): 敌手取任意的 \(\sigma\), 并计算 \(m=[\sigma^e\mod{N}]\) (\(e\) 是公钥)
  这样就 forge 出一对 \(([\sigma^e\mod{N}], \sigma)\): 虽然敌手无法对指定的 \(m\) 产生对应的签名，但是这样还是破坏了 Existential Unforgeability

• \(\geq 2\) query attack: Forging Signature on an arbitrary message
  对于确定的 \(m\)，敌手构造出 distinct \(m_1, m_2\) 使得 \(m=m_1m_2\mod{N}\)
  用 \(m_1, m_2\) 询问 signing oracle 得到 \(\sigma_1=[m_1^d\mod{N}], \sigma_2=[m_2^d\mod{N}]\)
  则计算 \(\sigma=\sigma_1\sigma_2=[(m_1m_2)^d\mod{N}]=[m^d\mod{N}]\)
  构造出 \((m, \sigma=\sigma_1\sigma_2)\)
  因此，在敌手拥有询问集 \(Q=\{m_1, m_2, ..., m_q\}\) 的情况下，敌手能构造出 \(2^q-q-1\) 个不同的 \((m, \sigma)\) 对

• Single query attack: Forging Signature on an arbitrary message
  前面介绍的方法需要询问 signing Oracle 至少两次；这里提供两种只需要询问一次的方法

  • 计算 \(m^{-1}\mod{N}\)，询问 \(\sigma=sign(m^{-1})=m^{-d}\mod{N}\)，这样构造出 \(m\) 的签名 \(m^d=\sigma^{-1}\)
    forge 出 \((m, \sigma^{-1})\)
  • 计算 \(m2^e\mod{N}\)，询问 \(\sigma=sign(m2^e)=(m2^e)^d=m^d2^{de}=m^d\)，直接构造出 \(m\) 的签名
    forge 出 \((m, \sigma)\)

• Weak definition of Security
  由于 Plain RSA Digital Signature 是不安全的，我们尝试放松安全的定义，给敌手施加更多的限制 (即，定义变弱)
  若 RSA 问题是困难的，Plain RSA Digital Signature 在该定义下安全:
  敌手获得公钥 \((N, e)\)，与一个 uniform (限制 \(1\)) 的信息 \(m\in \Z_N^*\)，敌手不能询问 (限制 \(2\)) signing oracle
  敌手胜利当且仅当对该特定的 \(m\) (限制 \(3\)) 能 forge 出一对 valid 的 \((m, \sigma)\)

Full Domain Hash (FDH)

为了应对上述的攻击，我们引入全域哈希 Full Domain Hash (FDH) 函数 \(H\)
我们可以将 \(H\) 看作是一个随机单向函数，将消息 \(m\) 随机的映射到 \(Z_N^*\) 中
\(H\) 也作为公钥的一部分 \(pk=(N, e, H)\)

• Authentication: \(\sigma=[H(m)^d\mod{N}]\)
• Verification: 输出 \(1\) 当且仅当 \(\sigma^e=H(m)\pmod{N}\)

这样利用 FDH 改进过的 RSA Digital Signature 方案称作 RSA-FDH Signature Scheme
该 FDH-RSA 方案由于引进了全域哈希函数 \(H\)，可以处理任意长度的信息 \(m\) ( \(H(m)\) 一定会将其映射在 \(Z_N^*\) )
注意：该方案并不属于 Hash-and-Sign Diagram，因为组成其的 Plain RSA Digital Signature 是不安全的

RSA-FDH Digital Signature Scheme

RSA-FDH Digital Signature Scheme: Security

有效的全域哈希函数 (RSA-FDH) 是一个随机预言机 (random oracle)，拥有以下性质

• A random function, which has range of sufficiently large size, is hard to invert
• A random function also does not satisfy multiplicative relations (很好理解，都随机化了，当然不会符合乘法关系), ans is collision resistant
• 重要: 若 \(x\) 并未被询问过，则 \(H(x)\) 一定是 uniform 的: 该性质与 PRG \(G\) 的性质不同，PRG \(G(x)\) 是 uniform 的当且仅当 \(x\) 是 uniformly chosen 的；而随机预言机 \(H\) 则没有这种限制；即使 \(x\) 并不是 uniformly chosen 的，结果 \(H(x)\) 也一定是 uniform 的 (使得 RSA Assumption 成立)

Attempting attack to RSA-FDH

接下来，我们尝试用之前 Plain RSA 的几种攻击方法来对 RSA-FDH 进行攻击

• 特殊 \(1\) 攻击
  \(1\) 的 \(d\) 次方一定是 \(1\)，而 \(H(1)\) 的 \(d\) 次方就很难计算了 (\(d\) 是私钥)
• 信息合成攻击
  在 Plain RSA 中，\(m\) 的签名 \(\sigma\) 是 \(m_1, m_2, \ (m=m_1m_2)\) 签名之积
  而在 RSA-FDH 中，该关系被破坏了: \(H(m)^d\) 不一定等于 \(H(m_1)^dH(m_2)^d\) (这是由于 \(H\) 不满足 multiplicative relations)
• 对随机信息的攻击
  在 Plain RSA 中，我们可以随机选择 \(\sigma\)，forge 出 \((\sigma^e, \sigma)\) 破坏 Plain RSA 的 Existential Unforgeability
  然而在 RSA-FDH 中不行: 随机选择 \(\sigma\)，对应的 \(m\) 满足 \(\sigma^e=H(m)\)
  而 \(H\) 是单向函数，也就是，给出 \(H(m)\)，想要 invert 得到 \(m\) 是困难的
  所以该攻击同样失效

Public-Key Identification Schemes

这里我们又将介绍一个新的加密 primitive: identification scheme
(已经有 encryption scheme，hash scheme，message authentication code，digital signatures, 现在又有了 identification scheme)
Identification 的目的是：一方 (prover) 通过 identification 向 另一方 (verifier) 证明自己的身份
一般来说，prover (拥有 \(pk, sk\)) 向 verifier (拥有 \(pk\)) 证明自己的身份，即，自己是 \(pk\) 的生成者

可以发现 Digital Signature 其实也能够提供 identification, 所以：

Identification schemes are building blocks for digital signature protodcols.

Public-key identification schemes: general idea

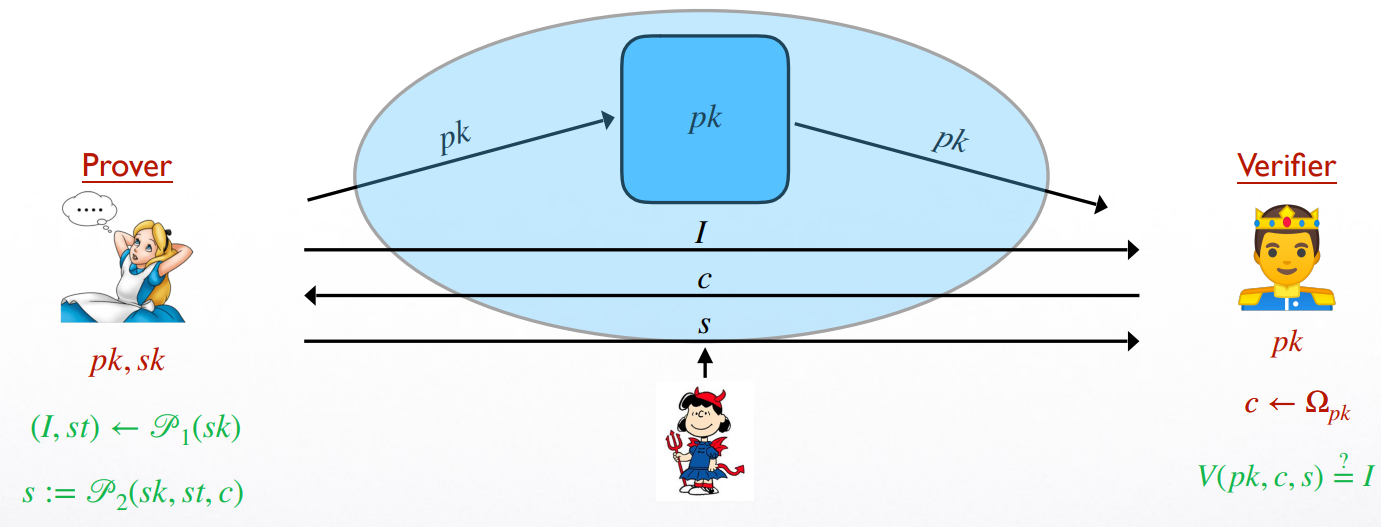
• non-degenerate:
  对于任意私钥 \(sk\) 与任意固定的初始 \(I\)，\(\Pr[\mathscr{P}_1(sk) outputs I]\) 是 negligible 的
  (这保证了 \(I\) 重复的概率是 negligible 的)
• Security requirement:
  若敌手不知道 prover 的私钥 \(sk\)，他将无法冒充 prover 的身份 (fool the verifier into accepting)

在敌手 passively 观察到多次该 protocol 的执行后，安全性仍有保证

Identification Experiment: 定义 identification scheme 的安全性

注意：敌手拥有 \(Trans_{sk}\) 的 oracle access! 也就是，每次敌手询问 \(Trans_{sk}\)，其都能获得一个 transcript \((I, c, s)\)

Security of identification scheme

注意，这里的敌手是 passive adversary
active adversary 需要更强的安全定义：对于 active adversary，它将会 冒充 verifier，与 prover 互动 (向 prover 发送 \(c\))
当然，在研究 identification scheme 在 digital signature 的应用中，我们只需要考虑被动敌手

From Identification Code to Digital Signature Scheme

这里我们介绍 Fiat-Shamir Transform: 它能将任意 interactive identification scheme 转化为 non-interactive signature scheme
(联想到在 exercise 中介绍的一种转换，能将任意密钥交换协议转化为公钥加密方案)

核心的转换在于: signer，同样也是 prover，自己产生 challenge \(c\)，并作为 signature 的一部分
即，将 identification scheme 作为 digital signature 的一个 subroutine
(之前介绍的转换也是将 key exchange protocol 作为 public key encryption 的一部分)

• 作为 digital signature scheme, Alice (signer) 拥有 \(m\) 与私钥 \(sk\)
• Alice (signer) 运行 Identification scheme，plays both parties
  在生成 \(I\) 后，又生成 \(c:=H(I,m)\) by applying \(H\)
• Alice (signer) 还计算对 \(c\) 的回应 \(s\)，且将 \((c,s)\) 作为 signature
• Bob (verifier) 在收到 \((m, \sigma=(c,s))\) 后，进行验证；
  第一步：Bob 使用公钥 \(pk\) 计算 \(I:=V(pk, c, s)\)
  第二步：计算 \(H(I,m)\) 是否等于 \(c\)，若是，则 accept；若不是，则 reject

Fiat-Shamir Transform: formal definition (重要)

定义有点小绕，多看几遍 (主要是 identification scheme 的定义)

Security of Signature scheme obtained from Fiat-Shamir Transform

• 安全的 identification scheme
• \(H\) 是 random oracle (随机 + one-way)

这里的 reduction 过程与 RSA-FDH 很相似，简述一下过程

构建 \(\mathscr{S}\): digital signature 敌手，目标为对一个未询问过的 \(m\) forge 出对应的 signature \(\sigma\)

若 \(H\) 不是 random oracle: 则 \(H\) 不具有 collision-resistant 性质
对 \((m, c=H(I, m), s)\), 能够找到一对 \(c=(I', m')\)，则很容易 forge 出 \(m'\) 的 signature \(\sigma'=(c, s)\)

若 \(H\) 是 random oracle: (构建到 secure identification scheme 的 reduction)

给定敌手 \(\mathscr{A}\): identification scheme 敌手，目标为对挑战 \(c\) 生成 valid 的回应 \(s\)

• 每当 \(\mathscr{A}\) 询问 \(Trans_{sk}\) Oracle，\(\mathscr{S}\) 用随机的 \(m\) 询问 \(Sign(\cdot)\) 得到 \(\sigma=(c, s)\)
  \(\mathscr{S}\) 计算 \(V(c, s, pk)=I\) 且将 \((I, c, s)\) 作为 transcript 回复给 \(\mathscr{A}\)
• 在某时刻 \(\mathscr{A}\) 将会输出一个 \(I\)，此时 \(\mathscr{S}\) 选择一个 \(m^*\notin Q\) 并计算 \(c^*=H(I,m)\) 并作为挑战回复给 \(\mathscr{A}\)
  \(\mathscr{A}\) 输出 \(s^*\) 作为对 \(c^*\) 的回应
  \(\mathscr{S}\) forge signature as \(\sigma^{*}=(c^*, s^{*})\)

Schnorr Identification Scheme

下面我们介绍一个建立在 Dlog 问题下的 identification scheme: Schnorr Identification Scheme

• 运行 \(Gen(1^n):=(pk, sk)\), 就像任意 Dlog 的 crypto primitive 一样，\(sk=x, pk=(G, q, g, h=g^x)\)
• Prover 生成 state \(r\in \Z_q\), 计算 \(I=g^r\) 并传送给 Verifier
• Verifier 生成 \(c\in \Z_q\) 作为挑战
• Prover 计算 \(s=cx+r\) 作为 response
• Verifier 计算 \(g^sh^{-c}\) 若 \(=I\) ，则 accept，反之 reject

Eavesdropping: No Advantages

在对 Identification scheme 的攻击中，敌手拥有对 \(Trans_{sk}\) 的 oracle access
然而，对 Schnorr Identification Scheme 的攻击中，拥有对 \(Trans_{sk}\) oracle access 与否并不会造成任何影响
因为敌手可以在不依赖 \(sk\) 的情况下，独立生成 transcript

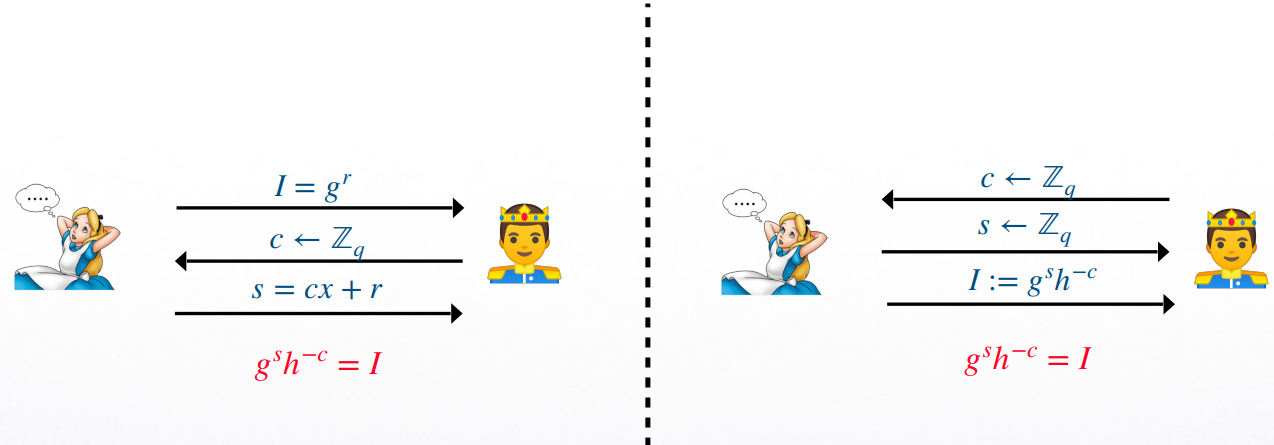
(左右过程是等价的：生成的 \((I, c, s)\) 拥有相同的分布 identical distribution)

在 transcript 生成的过程中，涉及的所有变量都是 完全随机 的
\(r\) 是随机的 \(\to\) \(I=g^r\) 是随机的
\(c，r, x\) 均是随机的 \(\to\) \(s=cx+r\) 是随机的
因此，敌手完全可以通过随机生成 \(c,s\in \Z_q\)，再计算 \(I=g^sh^{-c}\)

所以，敌手完全可以仅仅通过公钥 \(pk\) 生成任意的 transcript
拥有 \(trans_{sk}\) 的 oracle access (或 eavesdropping) 不会为敌手带来任何的 advantage

Schnorr Identification Scheme and DLog problem

首先，对于一个有效的 Schnorr Identification Scheme 的敌手，其一定也能解决 Discrete Logarithm 问题
敌手首先输出 \(I\):

• 敌手只能有效的回应一个挑战 \(c\)
  在该情况下，这个敌手并不是有效的敌手，其成功的概率仅有 \(\frac{1}{q}=\frac{1}{2^n}\) which is negligible
• 敌手能够回应两个以上的挑战 \(c_1, c_2 \ \ c_1\neq c_2\)
  在该情况下，敌手是有效的，且其能解决 \(\mathtt{DLog}\) 问题
  假设其作出的回应为 \(s_1, s_2\)
  则有 \(g^{s_1}h^{-c_1}=g^{s_2}h^{-c_2}=I\)
  整理得 \(\log_g h=[(s_1-s_2)\cdot (c_1-c_2)^{-1}\mod{q}]\)

Security of Schnorr Identification: formal definition

这个证明起来还是有点 tricky 的
首先，reduction 很好想

问题在于这里：我们构建的 \(\mathscr{S}\) 需要使用 \(\mathscr{A}\) 作为 subroutine
但是我们与 \(\mathscr{A}\) 交互的手段仅有 \(c\) 一种方式，其他的随机变量都是 \(\mathscr{A}\) 自己产生的
而为了解决 \(\mathtt{DLog}\) 问题，两次询问中其他所有随机量 (\(x\), \(r\), \(I\)) 等都必须是一致的
我们作为 \(\mathscr{S}\) 无法控制 \(\mathscr{A}\) 的内部机制 (抽象化)，所以只能依靠随机性来解决问题

我们用 \(\omega\) 来表示 除 \(c\) 之外 的所有随机量 (或是整体随机性 randomness)
而 \(V(\omega, c)=1\) 表示在挑战为 \(c\)，随机性为 \(\omega\) 时敌手 \(\mathscr{A}\) 作出了有效的回应
用 \(\delta_{\omega}\) 表示随机性为 \(\omega\) 时敌手 \(\mathscr{A}\) 成功回应的概率，则 \(\delta_{\omega}=\sum_{c}\Pr[V(\omega, c)=1]\)
那么 \(\Pr[\mathtt{Ident}_{\mathscr{A}, \Pi}(n)=1]=\Pr_{\omega, c}[V(\omega, c)=1]=\sum_{\omega} \Pr[\omega]\cdot \delta_{\omega}\) (相当于两个循环，先循环 \(\omega\)，再循环 \(c\))
定义 \(\delta(n)=\Pr[\mathtt{Ident}_{\mathscr{A}, \Pi}(n)=1]=\sum_{\omega} \Pr[\omega]\cdot \delta_{\omega}\)

而 \(\Pr[\mathtt{DLog}_{\mathscr{S}, \mathscr{G}}(n)=1]=\Pr_{\omega, c, c'}[(c\neq c') \and V(\omega, c)=1 \and V(\omega, c')=1]\) (枚举所有 \(\omega, c, c'\))

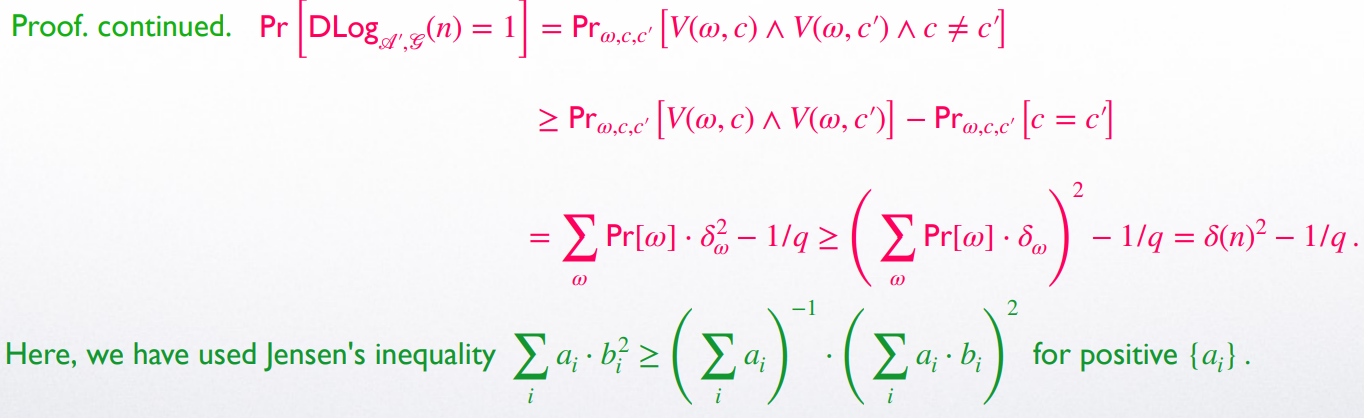
绕了好大一个圈子，终于将 \(\mathtt{Ident}\) 与 \(\mathscr{DLog}\) 实验联系起来了...
即 \(\Pr[\mathtt{DLog}_{\mathscr{S}, \mathscr{G}}(n)=1]\geq \Pr[\mathtt{Ident}_{\mathscr{A}, \Pi}(n)=1]^2-1/q\)
由于 \(\mathtt{DLog}\) 问题对于 \(\mathscr{G}\) 是困难的，我们有 \(\Pr[\mathtt{DLog}_{\mathscr{S}, \mathscr{G}}(n)=1]\leq \varepsilon(n)\) for negligible \(\varepsilon(n)\)
所以 \(\Pr[\mathtt{Ident}_{\mathscr{A}, \Pi}(n)=1]^2-1/q\leq \varepsilon(n)\)
又 \(\frac{1}{q}=\frac{1}{2^n}\) 同样是 negligible 的，因此 \(\Pr[\mathtt{Ident}_{\mathscr{A}, \Pi}(n)=1]\) 同样是 negligible 的
由此证明，当关于 \(\mathscr{G}\) 的 \(\mathtt{DLog}\) 问题困难时，Schnorr Identification Scheme 是安全的

Schnorr Digital Signature Scheme

Security of Schnorr Digital Signature Scheme

\(\mathtt{DLog}\) 的困难性 \(\to\) 对应 Schnorr Identification Scheme 的安全性
Schnorr Identification Scheme 的安全性 + \(H\) 是 random oracle \(\to\) Schnorr Digital Signature Scheme 的安全性 (Fiat-Shamir Transform)