[CF1753D]The Beach

做题时间：2022.10.24

\(【题目描述】\)

给定一个 \(n\times m(n,m\leq 3\times10^5,n\times m\leq 3\times 10^5)\) 的网格图，上面有的是空地，有的是障碍 # ，有的是大小为 \(1\times2\) 的床，现在可以花费 \(p(p\leq 10^9)\) 的代价将其中一个床绕其中某个点旋转 \(90°\)，也可以花费 \(q(q\leq 10^9)\) 的代价将其中一个床延长边移动一个单位。现在要腾出相邻的两个为空地的点，问最小代价是多少，或告知无解。

\(【输入格式】\)

第一行两个整数 \(n,m\)

第二行两个整数 \(p,q\)

接下来 \(n\) 行每行一个长为 \(m\) 的字符串，表示一个 \(n\times m\) 的网格图，其中 . 表示空地， # 表示障碍，L R U D 分别表示一张床的左边、右边、上面、下面的点

\(【输出格式】\)

第一行一个整数表示答案，若无解输出 -1

\(【考点】\)

最短路

\(【做法】\)

看到这种网格图上相邻两点成一体的题，可以想到网格图上奇偶染色，相邻的点归属不同的颜色，然后跑二分图，然后发现床的移动依然不好维护。

转化一下思路，因为最后要求的是得到相邻空地的代价，因此可以考虑维护空地的移动，对于一张床，我们可以花费 \(p\) 的代价旋转 \(90°\)，意味着可以将与床长边相邻的空地移动到不与其相邻的床上的点；花费 \(q\) 的代价延长边移动一格，意味着将与床短边相邻的空地移动到与其不相邻的床上的点。如图：

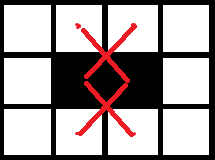
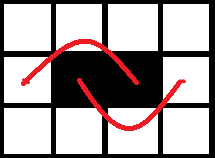
代价分别为 \(p\) 和 \(q\) 的移动（红色点为可移动空地，竖着的床同理）

然后通过观察会发现，移动只会发生在之前染成同一种颜色的点之间，即不同颜色的点的移动互不影响。最后求解的是相邻两点，也是不同颜色的。这启发我们将网格图上的每一个点看成图上的点，而可以移动的点之间连边（注意是单向边），长度即为移动代价，初始所有空地为起点，跑一遍最短路，求出图上所有相邻两个点到起点的最短距离之和即可。时间复杂度 \(\Theta(nm\log nm)\)

\(【代码】\)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=6e5+50;
typedef long long ll;
struct edge{
	int to,nxt,val;
}a[N<<1];
struct point{
	int num;
	ll val;
	bool operator <(const point &b) const{
		return val>b.val;
	}
};
ll dis[N];
int head[N],cnt,n,m,p,q;
priority_queue<point> que;
string s[N];
bool vis[N];
inline int id(int x,int y){return (x-1)*m+y;}
void add(int x,int y,int p,int q,ll w)
{
	if(x>n||x<1||p>n||p<1||y>m||y<1||q>m||q<1||s[x][y]=='#'||s[p][q]=='#') return ;
	int u=id(x,y),v=id(p,q);
	cnt++;
	a[cnt].to=v;
	a[cnt].val=w;
	a[cnt].nxt=head[u];
	head[u]=cnt;
}
void dijkstra()
{
	while(!que.empty()){
		int u=que.top().num;
		que.pop();
		if(vis[u]) continue;
		vis[u]=true;
		for(int i=head[u];i;i=a[i].nxt){
			int v=a[i].to;
			if(dis[v]>dis[u]+a[i].val){
				dis[v]=dis[u]+a[i].val;
				que.push((point){v,dis[v]});
			}
		}
	}
}
signed main()
{
	scanf("%lld%lld%lld%lld",&n,&m,&p,&q);
	memset(dis,9,sizeof dis);
	for(int i=1;i<=n;i++) cin>>s[i],s[i]='0'+s[i];
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(s[i][j]=='.') dis[id(i,j)]=0,que.push((point){id(i,j),0});
			if(s[i][j]=='L'){
				add(i-1,j+1,i,j,p);
				add(i+1,j+1,i,j,p);
				add(i-1,j,i,j+1,p);
				add(i+1,j,i,j+1,p);
                
				add(i,j-1,i,j+1,q);
				add(i,j+2,i,j,q);
			}
			if(s[i][j]=='U'){
				add(i,j-1,i+1,j,p);
				add(i,j+1,i+1,j,p);
				add(i+1,j-1,i,j,p);
				add(i+1,j+1,i,j,p);
				
				add(i+2,j,i,j,q);
				add(i-1,j,i+1,j,q);
			}
		}
	}
	dijkstra();
	ll ans=1e18;
//	for(int i=1;i<=n;i++){
//		for(int j=1;j<=m;j++){
//			printf("%d %lld\n",id(i,j),dis[id(i,j)]);
//		}
//		printf("\n");
//	}
//	for(int i=1;i<=n;i++){
//		for(int j=1;j<=m;j++) printf("%lld ",dis[id(i,j)]);
//		printf("\n");
//	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(i!=n) ans=min(ans,dis[id(i,j)]+dis[id(i+1,j)]);
			if(j!=m) ans=min(ans,dis[id(i,j)]+dis[id(i,j+1)]);
			
		}
	}
	if(ans>=1e16) printf("-1\n");
	else printf("%lld\n",ans);
	return 0;
}