[POJ3071]Football

做题时间：2022.8.9

\(【题目描述】\)

有 \(2^n(1\leq n\leq 7)\) 只足球队参加淘汰赛，编号为 \(1\rightarrow 2^n\) ，每轮淘汰赛相邻的未淘汰的队伍进行比赛，其中第 \(i\) 只队伍战胜第 \(j\) 只队伍的概率为 \(p_{i,j}\) ，一轮比赛完后胜利的队伍按照编号顺序排列，进行下一轮比赛。问最后哪一支队伍的胜率最大。

\(【输入格式】\)

多组数据，每组数据第一行一个数 \(n\)

第 \(2\rightarrow 2^n+1\) 行每行 \(2^n\) 个整数表示 \(p_{i,j}\)

输入末尾一个-1表示结束

\(【输出格式】\)

一行一个整数表示胜率最大的队伍编号

\(【考点】\)

概率DP

\(【做法】\)

定义 \(f_{i,j}\) 表示 第 \(i\) 只队伍第 \(j\) 轮比赛获胜的概率，枚举第 \(j\) 轮比赛中 \(i\) 的对手，有转移方程：

\[f_{i,j}=\sum\limits_{k在第j轮可能成为i的对手} f_{i,j-1}\times f_{k,j-1}\times p_{i,k} \]

接下来考虑 \(k\) 如何计算，如下：

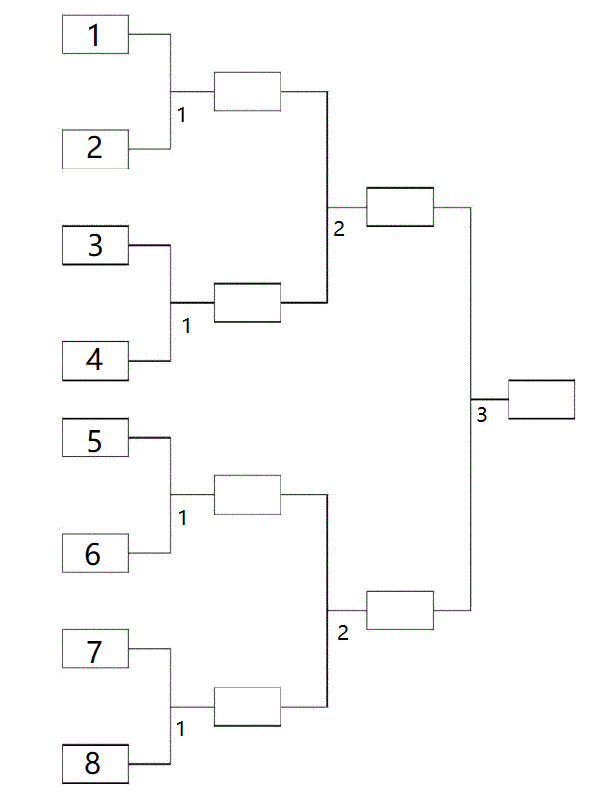
如图，\(4\) 号队伍在第2轮比赛中的对手只可能是 \(1\) 和 \(2\) 号队伍，而 \(5\) 号队伍在第3轮比赛的对手只可能是 \(1,2,3,4\) 号队伍……可以发现，一只队伍在第 \(j\) 轮比赛的对手是在将所有队伍分成长度为 \(2^{j-1}\) 的块及 \(2^j\) 的块后在同一个 \(2^j\) 且不在同一个 \(2^{j-1}\) 块内的所有队伍什么鬼 ，总之通过枚举可知，第 \(j\) 轮对手队伍总是连续的且区间长度为 \(2^{j-1}\) ，这些对手与 \(i\) 同处于一个 \(2^j\) 块，且不处于同一个 \(2^{j-1}\) 块，这样的区间在 \(i/2^{j-1}\) 为偶数时在 \(i\) 的左边相邻，为奇数时在 \(i\) 的右边相邻。

\(【代码】\)

#include<cstdio>
#include<iomanip>

using namespace std;
const int N=1<<8;
int n,t;
double f[N][N],p[N][N];
int main()
{
	scanf("%d",&n);
	while(n!=-1){
		for(int i=1;i<=(1<<n);i++){
			for(int j=1;j<=(1<<n);j++){
				scanf("%lf",&p[i][j]);
				f[i][j]=0.0;
			}
		}
		for(int i=1;i<=(1<<n);i++){
			if(i&1) f[i][1]=p[i][i+1];
			else f[i][1]=p[i][i-1];
            //初始化第一轮的胜率
		}
		for(int j=2;j<=n;j++){
			int len=(1<<j-1);//i在本轮的对手区间长度
			int l=len+1;//区间左端点
			for(int i=1;i<=(1<<n);i++){
				for(int k=l;k<l+len;k++) f[i][j]+=f[i][j-1]*f[k][j-1]*p[i][k];
				if(i%len==0){
					if(i/len%2==0) l+=len*3;//将区间移到i的右边
					else l-=len;//将区间移到i的左边
				}
			}
		}
		double maxn=0;
		int num=0;
		for(int i=1;i<=(1<<n);i++){
			if(f[i][n]>maxn) maxn=f[i][n],num=i;
		}
		printf("%d\n",num);
		scanf("%d",&n);
	}
	return 0;
}